Interpretable Neural Subgraph Matching for Graph Retrieval（用于图检索的可解释神经子图匹配）-论文笔记

Interpretable Neural Subgraph Matching for Graph Retrieval

作者：

会议：AAAI 2022

1. Background

给定一个查询图和一个数据图库，图检索系统旨在找到最相关的数据图。构建查询图与数据图之间的相关性模型是任何图检索系统的核心挑战，这主要依赖于全图或子图匹配、图核设计、图编辑距离（GED）和最大公共子图（MCS）。

基于子图匹配的图检索在许多应用中具有广泛的用途，例如分子指纹检测、电路设计、软件分析和问答系统。在这些应用中，当查询图（完全或近似）是数据图的一个子图时，该数据图被视为与查询图相关联。

2. Motivation

近来有大量研究提出了基于神经网络的图检索方法，这些方法采用了多种相关性度量，例如GED、MCS等。然而，这些方法在用于基于子图匹配的图检索时存在以下局限：

基于节点或图嵌入的对齐：现有的神经图检索模型通过比较查询图和数据图的节点或图嵌入来计算它们之间的相关性得分。然而，这类模型可能无法保证查询图和数据图之间的边一致性。
对称评分函数：这些模型通常采用对称的相关性得分，但在子图匹配的情境中，对称的相关性得分是不合适的，因为子图关系具有偏序性质（自反、反对称、传递性）。因此，在子图匹配方面，这些模型的检索性能较差。

子图相关性（SED）和常用的图相关性（GED）的区别：SED是不对称的，即 $SED(G_1,G_2)≠SED(G_2,G_1)$ ；而GED是对称的，即 $GED(G_1,G_2)=GED(G_1,G_2)$
对细粒度监督的需求：一些图匹配方法依赖于最优节点匹配的直接细粒度监督，这类训练数据的获取极其耗费精力。而实际的图检索系统可能仅提供查询-数据图对的二元相关标签。理想情况下，图检索系统应能够通过这种弱监督有效地学习相关性函数。
缺乏可解释性：理想情况下，图检索系统应能够通过近似的对齐关系来解释其相关性评分，而许多现有系统将每个图映射到一个单一的聚合向量，以此估计相似性得分，尽管表现出较高的表达能力和准确性，但它们缺乏可解释性。

3. Contribution

论文提出了一种新颖的、可解释的神经边对齐模型——ISONET。

可解释的边对齐网络：ISONET包含一个边对齐网络，能够学习数据图的边相对于给定查询图的最佳对齐方式。这使得ISONET相较于基于节点或图对齐的方法能更准确地预测子图关系，同时，模型具有可解释性，除了精确的检索外，该模型还能精确定位数据图中与查询图近似同构的子图。
非对称损失：边对齐网络的目标是最大化【数据图的边所覆盖的查询图的边的数量】。ISONET使用合页损失（hinge loss）来近似未覆盖的查询边数量，因此，语料库图中未匹配的部分不会影响相关性评分。
弱监督（Distant supervision）。ISONET可以在二元全图相关性指标的监督下，通过成对排名损失有效训练，而无需对节点或边对齐进行直接监督。

4. Preliminaries

我们有一个（无向）图集合 $D=Q∪C$ ，其中 $Q=\{G_q=(V_q,E_q)∣q∈[∣Q∣]\}$ 是查询图集合， $C=\{G_c=(V_c,E_c)∣c∈[∣C∣]\}$ 是数据图集合。此外，对于每个查询图 $G_q$ ，我们被给予一组相关图 $C_{q⊕}⊂C$ 和一组不相关图 $C_{q⊖}⊂C$ ，形式化定义如下：

C_{q⊕}=C \backslash C_{q⊖}=\{G_c∈C:G_q与G_c相关\} \tag{1}

在此情景下，如果 $G_c∈C_{q⊕}$ ，我们定义相关性标签 $y(G_q, G_c) = 1$ ，否则为0。我们使用 $G=(V,E)$ 表示 $Q∪C$ 中的任意图； $u_q, v_q$ 和 $u_c, v_c$ 分别表示查询图 $G_q$ 和数据库图 $G_c$ 的节点； $u, v$ 表示 $Q∪C$ 中任意图的节点。我们使用 $A_q, A_c$ 和 $A$ 表示图 $G_q, G_c$ 和 $G$ 的邻接矩阵。图中节点的排列记为 $S$ ，而边的排列记为 $P$ 。 $\mathbf{1}$ 表示全1张量。最后， $\text{vec}(A)$ 表示按列拼接 $A$ 后得到的向量， $⊗$ 表示矩阵的Kronecker积操作。

Kronecker积

设 $A$ 是 $m \times n$ 的矩阵， $B$ 是 $p \times q$ 的矩阵，那么它们的 Kronecker 积 $A \otimes B$ 是一个 $(mp) \times (nq)$ 的矩阵，定义为：
$A \otimes B = \begin{bmatrix} a_{11}B & a_{12}B & \cdots & a_{1n}B \\ a_{21}B & a_{22}B & \cdots & a_{2n}B \\ \vdots & \vdots & \ddots & \vdots \\ a_{m1}B & a_{m2}B & \cdots & a_{mn}B \end{bmatrix}$

5. Methodology

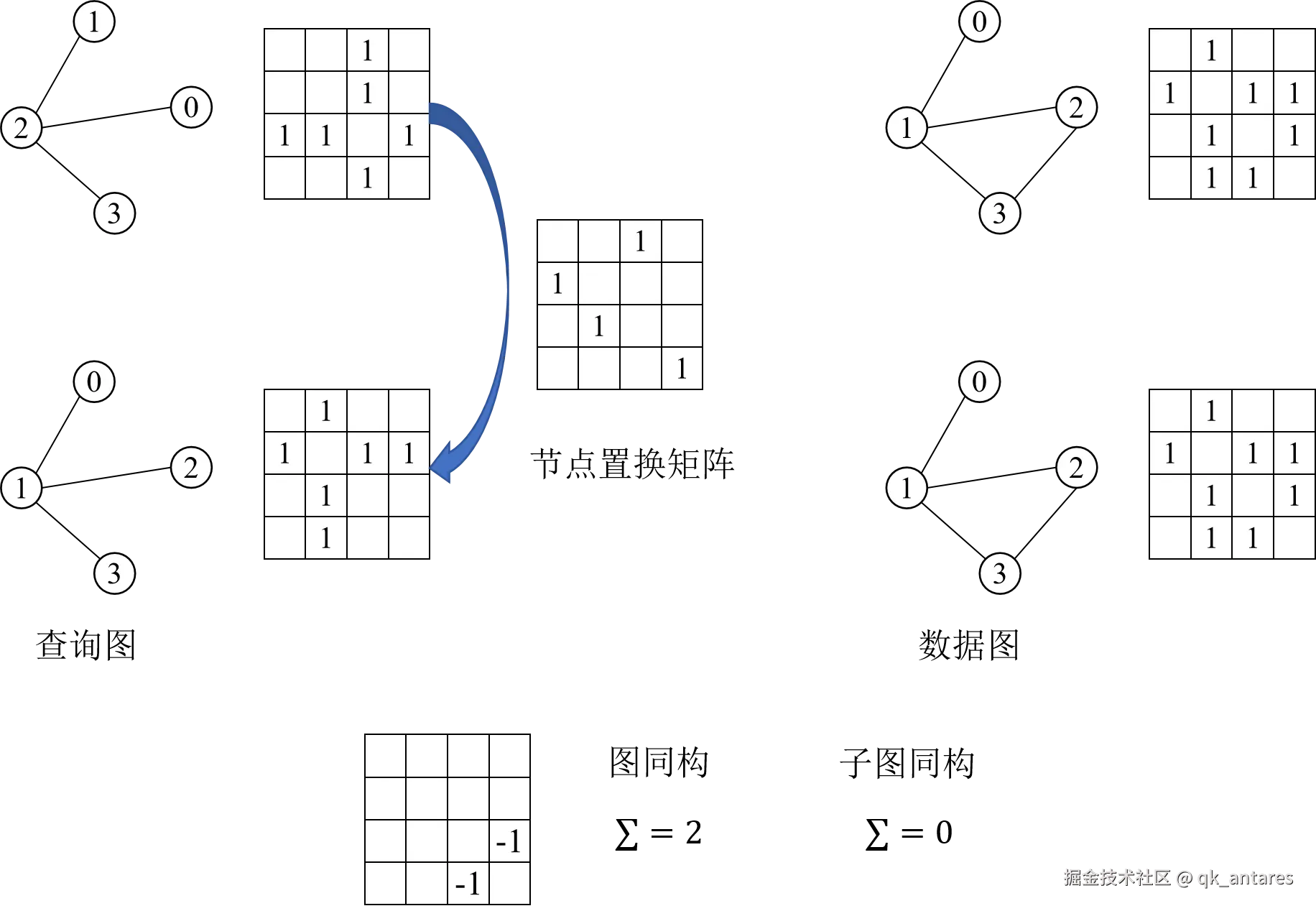
一个数据图 $G_c$ 如果包含一个与查询图 $G_q$ 同构的子图，则可以被视为对 $G_q$ 拥有“完美得分”，这对应于著名的NP完全问题——子图同构问题，另一个相关问题是图同构。

论文的目标仅涉及这些组合问题的连续松弛形式，以便更好地适应图检索任务。我们将首先从节点对齐的角度介绍图搜索，然后扩展到包含边的视角，以完成我们完整系统ISONET的设计。

5.1 节点对齐方法及其局限性

我们通过节点对齐构建一个距离得分，并说明其局限性，随后将在下一节中解决这些问题。

基于节点对齐的图同构（Graph isomorphism）测试。设 $V_q, V_c$ 分别为 $G_q, G_c$ 的节点集，一般情况下 $|V_q| < |V_c|$ 。我们通过添加 $|V_c| - |V_q|$ 个不相连的虚拟节点对 $G_q$ 进行填充。在它们的扩展形式中，设 $A_q$ 和 $A_c$ 为节点邻接矩阵（大小均为 $N$ ）。设 $S$ 是与 $A_q$ 和 $A_c$ 尺寸相同的节点置换矩阵，则 $S A_c S^\top$ 是 $A_c$ 的行列置换形式。图同构测试的目标是：

arg \min_S \| A_q - S A_c S^\top \|_F^2 \tag{2}

用于边覆盖的节点对齐。子图同构的情况有所不同。如果 $G_q \subseteq G_c$ ，则存在一个置换矩阵 $S$ ，使得 $A_q$ 中的每个非零元素在 $S A_c S^\top$ 中也是非零元素。换言之，可以通过优化以下目标实现子图同构测试：

\arg \min_S \sum_{i, j} [(A_q - S A_c S^T)_+]_{i, j} \tag{3}

其中 $(\cdot)_{+} = \{0,\cdot \}$ 是ReLU/合页函数。任何能将目标降到零的 $S$ 都可以验证子图同构，而该目标也可作为 $G_c$ 包含 $G_q$ 的接近度的相关性得分。

使用节点嵌入近似 $(3)$ 。在实际的图搜索应用中，节点和边的特征通常是连续且有噪声的。例如，在一个分子图中，查询分子中的氯原子可能近似匹配数据图中的功能类似的卤素如溴。为捕捉此类节点间的相似性，通常使用节点嵌入。设 $h_u \in \mathbb{R}^D$ 为节点 $u$ 的嵌入，节点嵌入矩阵 $H_q, H_c \in \mathbb{R}^{N \times D}$ 。如果存在 $S$ 使得 $H_q \approx S H_c$ ，则反映了对称相似性。但若如 $(3)$ 所示，我们希望检测语料库覆盖查询的情况，则需要 $H_q \leq S H_c$ （逐元素）：

d(G_c | G_q) = \min_S \sum_{i, j} [(H_q - S H_c)_+]_{i, j} \tag{4}

其中具有最小距离的 $G_c$ 对 $G_q$ 具有最高相关性得分，并在排名中排在首位。

局限性。节点对齐方法存在以下局限：

在图检索中， $d(G_q | G_c)$ 在训练时被输入到排序目标中。因此，我们需要在端到端训练中解决最小化问题 $(4)$ ，这要求一个可微分的计算最优节点置换 $S$ 的过程。然而，可微分的神经模块主要解决线性分配问题，而 $(4)$ 是一个著名的复杂的二次分配问题。
为了让 $(4)$ 能够合理近似 $(3)$ 并在节点对应间提供边一致性，节点 $u$ 的嵌入必须封装邻域信息。换言之，这些节点嵌入必须是上下文的。尽管采取了这些措施，我们的实验表明边覆盖问题必须直接处理，而不是依赖于上下文节点嵌入。下一步我们将发展这一思路。

5.2 从节点对齐到边对齐与覆盖

在这里，我们给出一种基于边对齐的子图匹配目标表示，以改进上述局限性。

使用边对齐的子图匹配。子图同构问题的难点之一在于需要节点置换来保持边的一致性或覆盖性。为了解决这个问题，我们在检索模型中直接强制边的一致性。我们通过将 $(3)$ 中的目标改写如下来说明这一点：

\sum_{i,j \in [N] \times [N]} [(A_q - S A_c S^\top)_+]_{i,j} \\ = \sum_{k \in [N^2]} \left[ \left( \text{vec}(A_q) - (S \otimes S) \text{vec}(A_c) \right)_+ \right]_k \tag{5}

这里， $N$ 是扩展图中的节点总数，方程 $(5)$ 中的 $\text{vec}(A_\bullet)$ 仅仅是所有 $N^2$ 边位置的边存在指示向量。

**用边嵌入近似 $(5)$ **。回到嵌入表示的世界，我们使用边嵌入而不是节点嵌入，记边 $e$ 的嵌入为 $r_e$ ，并将 $R_q, R_c \in \mathbb{R}^{|E| \times D}$ 表示为整体的边嵌入矩阵。我们可以类似于 $(4)$ 写出使用边嵌入的距离度量：

d(G_c | G_q) = \min_P \sum_e \left[ (R_q - P R_c)_+ \right]_e \tag{6}

其中 $P$ 是边的置换矩阵。从优化角度来看， $(6)$ 相较于 $(3)$ 的潜在优势在于避免了涉及 $S$ 的二次项，而不再包含二次项 $P$ 的计算复杂度。

5.3 ISONET架构

在这里，我们基于上述的边表示对齐构建我们的检索模型。我们使用两个神经网络近似方程 $(6)$ 中的 $d(G_c | G_q)$ 为 $( d_{\theta, \phi}(G_c | G_q)$ ，其中第一个网络（参数为 $\theta$ ）旨在提供底层优化问题的可微分解 $P^*$ ，而第二个网络（参数为 $\phi$ ）用于构建边表示矩阵 $R_q$ 和 $R_c$ 。

5.3.1 边嵌入 $R_\bullet$ 的神经网络设计

我们需要具体计算边嵌入矩阵 $R_q; R_c$ 。使用消息传递框架来学习上下文敏感的节点嵌入，这些嵌入随后用于计算边嵌入 $R_\bullet$ 。首先，对于每个节点 $u \in V$ ，我们将输入节点特征 $x_u$ 映射为初始节点嵌入：

h_u^{(0)} = \text{INIT}_{\phi}(x_u)

然后，给定一个整数 $K$ ，一个递归传播层用于聚合以每个节点为中心的 $K$ -跳子图的结构信息。在每个传播步骤（ $k \leq K$ ）中，为每条边 $(u, v) \in E$ 计算消息信号，并使用其邻居消息的聚合来更新节点嵌入：

r_{(v,u)}^{(k-1)} = \text{MSG}_{\phi} \left( h_v^{(k-1)}, h_u^{(k-1)} \right)

r_u^{(k-1)} = \text{AGGR}_{\phi} \left\{ r_{(v,u)}^{(k-1)} | v \in \text{nbr}(u) \right\}

h_u^{(k)} = \text{COMB}_{\phi} \left( h_u^{(k-1)}, r_u^{(k-1)} \right)

以上网络的所有可训练参数均记作 $\phi$ ，最终的上下文边嵌入矩阵为 $R = [r_{(u,v)}^{(K)}]_{(u,v) \in E}$ 。我们使用两个多层感知机（MLP）来实现初始嵌入计算网络 INIT 和消息传递网络 MSG。虽然 AGGR 可以是任何对称算子，此处我们使用简单的求和操作。最后，COMB使用门控循环单元（GRU）。

5.3.2 计算 $P^*$ 的网络设计

方程 $(6)$ 中的矩阵 $P$ 是一个“硬”置换矩阵。下一步是将 $P$ 放松为一个双随机矩阵或“软”置换矩阵，它将作为网络 $F_{\theta}(R_q; R_c)$ 的输出，其中 $\theta$ 是可训练参数。换句话说，将离散 $P$ 的组合搜索替换为松弛形式：

d_{\theta, \phi}(G_c | G_q) = \sum_{i,j} \left[ R_q - F_{\theta}(R_q; R_c) R_c \right]^+_{i,j} \tag{7}

由于存在ReLU()项，优化问题 $(6)$ 仍然不完全是线性分配问题。然而，下面我们表明，它可以在不含合页操作符的对偶空间中视为线性分配问题。具体而言，我们将方程 $(6)$ 的最小化问题的对偶形式写为：

\max_{C \in [0,1]} \min_P \text{Trace} \left( C^\top \left( R_q - P R_c \right) \right) \tag{8}

优化问题，即最小化目标函数
$\min_P \sum_{i,j} \left[ (R_q - P R_c) \right]_{i,j}^+$
这里的目标是找到一个排列矩阵 $P$ ，使得元素的正部分（用 $(\cdot)^+$ 表示，即 ReLU 函数）之和最小。这个优化问题可以重新表示为如下问题：
$\min_{P, \zeta \geq 0} \sum_{i,j} \zeta_{i,j} \quad \text{subject to} \quad \zeta_{i,j} \geq (R_q - P R_c)_{i,j}$
这个等价转换通过引入辅助变量 $\zeta_{i,j}$ 来放松目标函数。

对偶问题的构建：引入拉格朗日乘子矩阵 $C \geq 0$ 和 $D \geq 0$ 后，上述优化问题的对偶形式可以写为：
$\max_{C \geq 0, D \geq 0} \min_{P, \zeta \geq 0} \sum_{i,j} \zeta_{i,j} + C_{i,j} (R_q - P R_c - \zeta)_{i,j} - D_{i,j} \zeta_{i,j}$
通过引入拉格朗日乘子，转化成了一个极小极大问题，目的是引入松弛条件以便求解。

对 $\zeta_{i,j}$ 的微分：接下来，对 $\zeta_{i,j}$ 求偏导数，得到
$1 - C_{i,j} - D_{i,j} = 0 \Rightarrow C_{i,j} + D_{i,j} = 1$
因为 $D_{i,j} \geq 0$ ，因此 $C_{i,j}$ 的取值范围在 $[0, 1]$ 之间。

得到线性分配问题：根据以上条件，我们得到
$\max_{C \in [0, 1]} \min_P \sum_{i,j} C_{i,j} (R_q - P R_c)_{i,j} = \max_{C \in [0,1]} \min_P \text{Trace} \left[ C^T (R_q - P R_c) \right]$
这表明原始问题的求解可以通过一个线性分配问题来完成，即在 $C$ 的范围内最大化目标函数的迹。

其中 $C_{i,j}$ 是拉格朗日乘子。假设我们可以计算出最优 $C^* = C^*(R_q; R_c)$ ，则内层的最小化问题变为：

\min_P \text{Trace}[-P^\top C^*(R_q; R_c) R_c^\top] \tag{9}

因此，上述优化问题是一个具有成本矩阵 $C^*(R_q; R_c) R_c^\top$ 的线性分配问题。为近似此项，我们首先分别将 $R_q$ 和 $R_c$ 输入一个线性-ReLU-线性（LRL）网络（参数共享），然后执行内积计算原始的两两相似度。接着，这些相似度用于一个（软）置换查找器网络，我们采用可微的Gumbel-Sinkhorn操作符“GS”：

F_{\theta}(R_q; R_c) = \text{GS} \left( \text{LRL}_{\theta}(R_q) \cdot \text{LRL}_{\theta}(R_c)^T \right) \tag{10}

线性分配问题的示例：

$r=(3,3,3,4,2,2,2,1)^T \in R^n$ 代表每个工地上沙堆的需求量，

$c=(4,2,6,4,4) \in R^m$ 代表每个沙厂可以提供的沙，

$M \in R^{n×m}$ 代表代价矩阵（工厂运输沙到工地的成本）

$P \in R^{n×m}_{\geq{0}}$ 是一个分配矩阵， $U(r,c)=\{P|P1_m=r,P^T1_n=c\}$ 是空间， $1_m \in R^{m×1}$

最优运输即求一个分配矩阵 $d_M(r,c)$ ，使得总运输代价最小：

$d_M(r,c)=\min_{p \in U(r,c)} \sum _{ij} P_{ij}M_{ij}$

线性分配问题的近似求解：

Input: $M,r,c,\lambda$

Initialize: $(P_\lambda)_{ij}=e^{-\lambda M_{ij}}$

Loop:
Scale每一行，使横向求和是r
Scale每一列，使纵向求和是c
Until 收敛

GS的作用是找到一个线性分配问题的近似解，其成本矩阵作为输入。因而，在我们的设置中， $F_{\theta}$ 近似 $P^*$ ，即解决问题 $(9)$ 的最优置换矩阵。更具体地说，GS网络在一个初始温度 $\tau > 0$ 下，对输入矩阵 $M$ 进行交替的行列缩放：

\text{GS}(M) := \lim_{t \to \infty} \text{GS}^t(M),其中 \tag{11}

\text{GS}^0(M) = \exp(M / \tau) \tag{12}

\text{GS}^t(M) = \text{ColScale} \left( \text{RowScale} \left( \text{GS}^{t-1}(M) \right) \right) \tag{13}

5.3.3 评分、排序损失和训练

ISONET的一大显著特性在于，我们不需要细致的监督信息（如查询图 $G_q$ 与数据图 $G_c$ 之间的最优对齐关系）。相反，我们的训练实例仅包含一个查询图及其有限的相关和不相关语料库图集合 $C_q^+$ 和 $C_q^-$ 。沿用学习排序的相关研究，我们采用了一种成对排序损失函数。如果 $G_c^+$ 和 $G_c^-$ 分别是查询图 $G_q$ 的相关和不相关图，则我们希望满足以下条件：

d_{\theta, \phi}(G_c^+ | G_q) \ll d_{\theta, \phi}(G_c^- | G_q)

其中下标 $\theta$ 和 $\phi$ 表示评分函数的设计。我们通过带有超参数 $\gamma > 0$ 的合页损失（hinge loss）实现对 $\theta$ 的整体训练：

\min_{\theta, \phi} \sum_{G_q} \sum_{G_{c⊕},G_{c⊖}} \left[ \gamma + d_{\theta, \phi}(G_{c⊕} | G_q) - d_{\theta, \phi}(G_{c⊖} | G_q) \right]_+

Interpretable Neural Subgraph Matching for Graph Retrieval（用于图检索的可解释神经子图匹配）-论文笔记