向量检索核心算法——相似性度量

在我们的日常生活中，搜索和匹配是非常常见的事情。比如，你在网上购物时想找到与某件衣服相似的款式；在听音乐时想找到风格相近的歌曲；或者在阅读一篇文章后，想找到内容相关的其他文章或新闻。这些都离不开一个重要的概念：向量相似性度量。今天，我们将用简单的语言来解释这个概念，让即使只有初中数学水平的读者也能理解。

什么是向量？

首先，了解什么是向量。向量可以看作是一组数字的集合，这些数字代表了某个对象的特征。例如：

• 图片：一张图片可以被转换成一个向量，向量中的每个数字代表了图片的颜色、亮度等特征。
• 歌曲：一首歌可以被转换成一个向量，包含节奏、音调、风格等信息。
• 文本：一段文字可以被转换成一个向量，表示其中的词语频率、主题等特征。

通过将对象转换为向量，我们就可以用数学方法来比较它们的相似性。

为什么需要相似性度量？

当我们有很多向量时，想要找到与某个特定向量最相似的那些，这就是向量检索。为了判断两个向量有多相似，我们需要一种方法来度量它们之间的“距离”或“相似程度”，这就是相似性度量的作用。

举例：

• 购物推荐：你买了一本关于科幻小说的书，希望找到类似的书籍。通过将书的内容转换为向量，我们可以计算它与其他书籍的相似性，找到内容相近的推荐给你。
• 文本搜索：你在搜索引擎中输入“如何学习数学”，系统会将你的搜索词转换为向量，与数据库中文章的向量进行比较，找出最相关的文章。

常见的相似性度量方法

下面，我们介绍几种常见的向量相似性度量方法。

1. 欧氏距离（Euclidean Distance）

概念：
欧氏距离是最常见的距离度量方法，类似于我们在日常生活中计算两点之间的直线距离。比如，我们可以通过直线距离判断两个地点在地图上有多远。这个方法可以拓展到更高维度的数据中，用来计算向量之间的距离。

一维空间中的欧氏距离

在一维空间中，欧氏距离就是两点之间的绝对差值。假设有两个点 $A = x_1$和 $B = x_2$，它们的欧氏距离为：

举例： 假设 $A = 3$ 和$B = 7$ ，它们的欧氏距离为：

如下图所示：

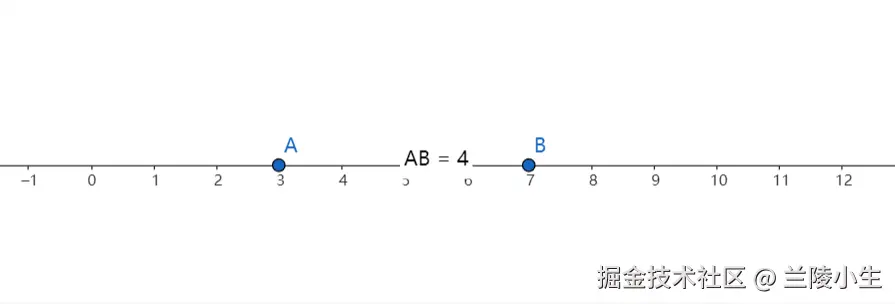这表示在一条直线上，点 $A$ 和点 $B$ 之间的距离是 4 个单位。

二维空间中的欧氏距离

在二维空间中，两个点有 $x$ 和 $y$ 两个坐标值。我们可以通过毕达哥拉斯定理来计算它们之间的距离。假设两个点 $A = (x_1, y_1)$和 $B = (x_2, y_2)$，它们之间的欧氏距离为：

如下图所示：

举例： 假设 $A = (3, 4)$ 和 $B = (7, 1)$，它们的欧氏距离为：

因此，点 $A$ 和点 $B$ 之间的距离是 5 个单位。

三维空间中的欧氏距离

在三维空间中，我们可以通过扩展二维空间的距离公式，计算出带有 $x$、$y$、$z$ 三个坐标的点之间的距离。假设两个点 $A = (x_1, y_1, z_1)$ 和 $B = (x_2, y_2, z_2)$，它们之间的欧氏距离为：

举例： 假设 $A = (1, 2, 3)$ 和 $B = (4, 6, 8)$，它们的欧氏距离为：

高维空间中的欧氏距离

高维空间中的距离计算与一维、二维和三维的原理相同，扩展到任意维度。假设我们有两个点 $A = (A_1, A_2, \dots, A_n)$ 和 $B = (B_1, B_2, \dots, B_n)$，它们的欧氏距离为：

举例： 假设我们有两个五维向量 $A = (1, 2, 3, 4, 5)$ 和 $B = (5, 4, 3, 2, 1)$，它们的欧氏距离为：

为什么欧氏距离可以表示相似性？

欧氏距离的原理来自平面几何中的毕达哥拉斯定理（勾股定理）。在二维空间中，给定两个点，我们可以通过水平和垂直方向上的距离来构成一个直角三角形，而直线距离则是斜边的长度。将这个思想推广到三维甚至更高维的向量空间，欧氏距离度量的就是两个点（向量）之间的最短路径，或“直线”距离。

设想我们有两个物体（例如两张图片），每个物体都可以用一系列特征来描述。比如说，一张图片可以用RGB颜色的值来表示。我们将这些特征作为向量的分量，当我们比较这两个物体的特征时，计算它们之间的欧氏距离就是通过比较这些特征的差异，来判断它们的“相似性”。距离越小，表明这两个物体的特征越接近，即越相似；反之，距离越大，差异也越大。

计算方法：
对于两个向量 $A$ 和 $B$，欧氏距离计算它们对应元素差的平方和的平方根。这个公式来自我们在二维几何中使用的直线距离公式，经过扩展，应用于高维空间。

这个公式可以理解为，在每个特征维度上计算两个向量的差值，然后对这些差值平方并累加，最终取平方根得到总体差异（即距离）。

在机器学习、图像处理和推荐系统等领域中，高维空间的欧氏距离被广泛用于衡量数据点之间的相似性。

总结

欧氏距离从一维到高维空间的扩展，都是通过计算每个维度上的差异来衡量两个点之间的相似性。在一维空间中，欧氏距离仅仅是两点之间的绝对差值；在二维和三维空间中，欧氏距离通过几何关系计算出两点的直线距离；而在高维空间中，欧氏距离仍然基于相同的原理，可以有效地度量复杂数据之间的差异。

2. 余弦相似度（Cosine Similarity）

概念：
余弦相似度是一种衡量两个向量之间夹角余弦值的方法，用于反映它们方向的相似性，而不考虑它们的大小。简单来说，余弦相似度关注的是两个向量的方向是否相似，而不关心它们的长度。这种方法在高维数据分析中尤为常用，如文本分析、图像处理和推荐系统等。

为什么余弦相似度可以表示相似性？
余弦相似度的原理来源于三角学中的余弦定理。通过计算两个向量之间的夹角余弦值，可以有效地衡量它们在方向上的相似性。当两个向量的方向完全一致时，余弦相似度为1，表示它们高度相似；当两个向量垂直时，余弦相似度为0，表示它们没有相似性；当两个向量方向相反时，余弦相似度为-1，表示它们完全不相似。

点积与余弦相似度的关系

要理解为什么余弦相似度是通过两个向量的点积除以它们模的乘积来计算的，首先需要了解点积和向量的模的几何含义，以及它们与向量夹角之间的关系。

点积的代数定义

代数上，两个向量 $\mathbf{A} = (A_x, A_y)$ 和 $\mathbf{B} = (B_x, B_y)$ 的点积定义为：

点积的几何定义

从几何角度，两个向量的点积也可以表示为：

其中，$\theta$ 是向量 $\mathbf{A}$ 和 $\mathbf{B}$ 之间的夹角，$\|\mathbf{A}\|$ 和 $\|\mathbf{B}\|$ 分别是向量 $\mathbf{A}$ 和 $\mathbf{B}$ 的模（长度）。

点积几何意义的推导

为了理解代数上的点积如何等于几何上的表达式，我们可以通过二维坐标系中的具体例子进行详细推导。

步骤一：绘制向量并构建三角形

1. 绘制向量：

   • 在二维坐标系中，绘制向量 $\mathbf{A} = (A_x, A_y)$ 和向量 $\mathbf{B} = (B_x, B_y)$。
   • 向量 $\mathbf{A}$ 从原点 $O(0,0)$ 指向点 $P(A_x, A_y)$。
   • 向量 $\mathbf{B}$ 从原点 $O(0,0)$ 指向点 $Q(B_x, B_y)$。

2. 构建三角形：

   • 将向量 $\mathbf{A}$ 的终点 $P$ 和向量 $\mathbf{B}$ 的终点 $Q$ 连接起来，形成三角形 $OPQ$。
   • 夹角 $\theta$ 就是向量 $\mathbf{A}$ 和向量 $\mathbf{B}$ 之间的角度。

如下图所示：

步骤二：向量 $\mathbf{A}$ 在向量 $\mathbf{B}$ 方向上的投影

1. 定义投影：

   • 向量 $\mathbf{A}$ 在向量 $\mathbf{B}$ 方向上的投影长度为：

     $$\text{投影长度} = \|\mathbf{A}\| \cos(\theta)$$

   • 这表示了向量 $\mathbf{A}$ 在向量 $\mathbf{B}$ 方向上的“分量”。

2. 构造投影向量：

   • 向量 $\mathbf{B}$ 的单位向量（长度为1的向量）为：

     $$\mathbf{u}_B = \left( \frac{B_x}{\|\mathbf{B}\|}, \frac{B_y}{\|\mathbf{B}\|} \right)$$

   • 向量 $\mathbf{A}$ 在 $\mathbf{B}$ 方向上的投影向量为：

     $$\mathbf{A}_{\parallel \mathbf{B}} = \|\mathbf{A}\| \cos(\theta) \cdot \mathbf{u}_B$$

步骤三：点积的几何意义

1. 点积与投影的关系：

   • 点积 $\mathbf{A} \cdot \mathbf{B}$ 可以看作是向量 $\mathbf{A}$ 在向量 $\mathbf{B}$ 方向上的分量与向量 $\mathbf{B}$ 的长度的乘积：

     $$\mathbf{A} \cdot \mathbf{B} = \|\mathbf{A}\| \cos(\theta) \cdot \|\mathbf{B}\|$$

   • 这个表达式表示了向量 $\mathbf{A}$ 在向量 $\mathbf{B}$ 方向上的分量（即 $\|\mathbf{A}\| \cos(\theta)$）乘以向量 $\mathbf{B}$ 的长度（即 $\|\mathbf{B}\|$）。

2. 解释：

   • 当两个向量方向相同（即 $\theta = 0^\circ$），$\cos(\theta) = 1$，点积达到最大值 $\|\mathbf{A}\| \|\mathbf{B}\|$，表示高度相似。
   • 当两个向量垂直（即 $\theta = 90^\circ$），$\cos(\theta) = 0$，点积为0，表示它们在方向上完全不相关。
   • 当两个向量方向相反（即 $\theta = 180^\circ$），$\cos(\theta) = -1$，点积为 $-\|\mathbf{A}\| \|\mathbf{B}\|$，表示它们在方向上完全相反。

步骤四：结合代数定义验证等价性

为了证明代数定义的点积等于几何定义的表达式，我们需要将代数公式转化为几何公式，或反之。

1. 代数定义：

   $$\mathbf{A} \cdot \mathbf{B} = A_x B_x + A_y B_y$$

2. 几何定义：

   $$\mathbf{A} \cdot \mathbf{B} = \|\mathbf{A}\| \|\mathbf{B}\| \cos(\theta)$$

3. 推导代数定义等于几何定义：

   • 计算向量的模：

     向量 $\mathbf{A} = (A_x, A_y)$ 的模：

     $$\|\mathbf{A}\| = \sqrt{A_x^2 + A_y^2}$$

     向量 $\mathbf{B} = (B_x, B_y)$ 的模：

     $$\|\mathbf{B}\| = \sqrt{B_x^2 + B_y^2}$$

   • 应用余弦定理：

     在三角形 $OPQ$ 中，应用余弦定理：

     $$\|\mathbf{A} - \mathbf{B}\|^2 = \|\mathbf{A}\|^2 + \|\mathbf{B}\|^2 - 2 \|\mathbf{A}\| \|\mathbf{B}\| \cos(\theta)$$

   • 展开左边的模平方：

     $$\|\mathbf{A} - \mathbf{B}\|^2 = (A_x - B_x)^2 + (A_y - B_y)^2$$

     展开平方：

     $$= A_x^2 - 2 A_x B_x + B_x^2 + A_y^2 - 2 A_y B_y + B_y^2$$

   • 展开右边的模平方：

     $$\|\mathbf{A}\|^2 + \|\mathbf{B}\|^2 - 2 \|\mathbf{A}\| \|\mathbf{B}\| \cos(\theta) = A_x^2 + A_y^2 + B_x^2 + B_y^2 - 2 \|\mathbf{A}\| \|\mathbf{B}\| \cos(\theta)$$

   • 比较两边：

     左边：

     $$A_x^2 - 2 A_x B_x + B_x^2 + A_y^2 - 2 A_y B_y + B_y^2$$

     右边：

     $$A_x^2 + A_y^2 + B_x^2 + B_y^2 - 2 \|\mathbf{A}\| \|\mathbf{B}\| \cos(\theta)$$

   • 消去相同项：

     将左边和右边的相同项（$A_x^2, A_y^2, B_x^2, B_y^2$）消去，得到：

     $$-2 A_x B_x - 2 A_y B_y = -2 \|\mathbf{A}\| \|\mathbf{B}\| \cos(\theta)$$

   • 简化方程：

     两边同时除以 $-2$，得到：

     $$A_x B_x + A_y B_y = \|\mathbf{A}\| \|\mathbf{B}\| \cos(\theta)$$

   • 最终结果：

     这证明了代数定义的点积 $\mathbf{A} \cdot \mathbf{B} = A_x B_x + A_y B_y$ 与几何定义的点积 $\mathbf{A} \cdot \mathbf{B} = \|\mathbf{A}\| \|\mathbf{B}\| \cos(\theta)$ 是等价的。

步骤五：具体示例验证

让我们通过一个具体的例子来验证这一推导过程的正确性。

• 示例：

  设向量 $\mathbf{A} = (3, 4)$ 和向量 $\mathbf{B} = (1, 0)$。

• 代数计算点积：

  $$\mathbf{A} \cdot \mathbf{B} = 3 \times 1 + 4 \times 0 = 3$$

• 计算向量的模：

  $$\|\mathbf{A}\| = \sqrt{3^2 + 4^2} = \sqrt{9 + 16} = \sqrt{25} = 5$$
  $$\|\mathbf{B}\| = \sqrt{1^2 + 0^2} = \sqrt{1} = 1$$

• 几何定义计算余弦值：

  根据几何定义：

  $$\mathbf{A} \cdot \mathbf{B} = \|\mathbf{A}\| \|\mathbf{B}\| \cos(\theta)$$

  将已知值代入：

  $$3 = 5 \times 1 \times \cos(\theta)$$

  解得：

  $$\cos(\theta) = \frac{3}{5} = 0.6$$

• 几何角度计算：

  余弦值 $\cos(\theta) = 0.6$ 对应的夹角：

  $$\theta = \cos^{-1}(0.6) \approx 53.13^\circ$$

• 验证等价性：

  通过代数和几何方法计算得到的点积值一致，验证了代数定义的点积与几何定义的点积之间的等价性。

余弦相似度的计算方法

余弦相似度是通过两个向量的点积除以它们模的乘积来计算的。这一方法能够有效地衡量两个向量在方向上的相似性，而不受它们长度的影响。

公式：

其中，

• $\mathbf{A} \cdot \mathbf{B} = A_x B_x + A_y B_y$ 是两个向量的点积。
• $\|\mathbf{A}\| = \sqrt{A_x^2 + A_y^2}$ 和 $\|\mathbf{B}\| = \sqrt{B_x^2 + B_y^2}$ 分别是向量 $\mathbf{A}$ 和 $\mathbf{B}$ 的模（长度）。

具体步骤：

1. 计算点积：

   对于向量 $\mathbf{A} = (A_x, A_y)$ 和 $\mathbf{B} = (B_x, B_y)$，计算它们的点积：

   $$\mathbf{A} \cdot \mathbf{B} = A_x B_x + A_y B_y$$

2. 计算向量模：

   计算每个向量的模（长度）：

   $$\|\mathbf{A}\| = \sqrt{A_x^2 + A_y^2}$$
   $$\|\mathbf{B}\| = \sqrt{B_x^2 + B_y^2}$$

3. 计算余弦相似度：

   将点积除以两个向量模的乘积：

   $$\text{余弦相似度} = \frac{A_x B_x + A_y B_y}{\sqrt{A_x^2 + A_y^2} \times \sqrt{B_x^2 + B_y^2}}$$

举例说明：

• 文本相似性：
  假设有两篇文章 $A$ 和 $B$，经过文本处理后得到词频向量 $\mathbf{A} = (1, 1, 0, 0)$ 和 $\mathbf{B} = (1, 0, 1, 0)$，表示在四个关键词上的词频。

  • 点积计算：

    $$\mathbf{A} \cdot \mathbf{B} = 1 \times 1 + 1 \times 0 + 0 \times 1 + 0 \times 0 = 1$$

  • 向量模计算：

    $$\|\mathbf{A}\| = \sqrt{1^2 + 1^2 + 0^2 + 0^2} = \sqrt{2}$$
    $$\|\mathbf{B}\| = \sqrt{1^2 + 0^2 + 1^2 + 0^2} = \sqrt{2}$$

  • 余弦相似度计算：

    $$\text{余弦相似度} = \frac{1}{\sqrt{2} \times \sqrt{2}} = \frac{1}{2} = 0.5$$

  这说明两篇文章有一定的相似性，余弦相似度越接近1，表示相似度越高；越接近0，表示相似度越低。

余弦相似度的优点

1. 方向性而非长度：
   余弦相似度只关注向量的方向，不关心它们的长度，因此非常适合用于文本、图像等特征向量的相似性度量。

2. 高维适用：
   在高维数据中，余弦相似度可以有效地用于比较两个高维向量的方向相似性，特别是在文本处理中，余弦相似度广泛应用于度量文章、段落或词语之间的相似性。

3. 数值稳定性：
   由于余弦值总是在 -1 和 1 之间，计算结果相对稳定，不会因为数据量大或向量的大小而产生极端值。

具体示例验证

让我们通过一个具体的例子来验证余弦相似度的计算过程。

• 示例：

  设向量 $\mathbf{A} = (3, 4)$ 和向量 $\mathbf{B} = (1, 0)$。

• 代数计算点积：

  $$\mathbf{A} \cdot \mathbf{B} = 3 \times 1 + 4 \times 0 = 3$$

• 计算向量模：

  $$\|\mathbf{A}\| = \sqrt{3^2 + 4^2} = \sqrt{9 + 16} = \sqrt{25} = 5$$
  $$\|\mathbf{B}\| = \sqrt{1^2 + 0^2} = \sqrt{1} = 1$$

• 几何定义计算余弦值：

  根据几何定义：

  $$\mathbf{A} \cdot \mathbf{B} = \|\mathbf{A}\| \|\mathbf{B}\| \cos(\theta)$$

  将已知值代入：

  $$3 = 5 \times 1 \times \cos(\theta)$$

  解得：

  $$\cos(\theta) = \frac{3}{5} = 0.6$$

• 几何角度计算：

  余弦值 $\cos(\theta) = 0.6$ 对应的夹角：

  $$\theta = \cos^{-1}(0.6) \approx 53.13^\circ$$

• 验证等价性：

  通过代数和几何方法计算得到的点积值一致，验证了代数定义的点积与几何定义的点积之间的等价性。

总结

余弦相似度通过计算两个向量之间的夹角余弦值来衡量它们的相似性。其计算方法是将两个向量的点积除以它们模的乘积，这一过程不仅结合了向量的代数定义，还基于几何角度的余弦定理推导而来。余弦相似度特别适合用于高维数据分析，因为它只关注向量的方向而不受向量长度的影响。

应用场景：

• 文本搜索与推荐：在搜索引擎中，通过计算查询词向量与文档向量的余弦相似度，找到最相关的文档。
• 图像相似性：在图像处理领域，通过比较图像特征向量的余弦相似度，找到相似的图片。
• 推荐系统：根据用户行为向量与物品特征向量的余弦相似度，推荐用户可能感兴趣的物品。

通过理解和应用余弦相似度，我们能够在各种数据密集型领域中有效地衡量和发现数据之间的相似性，从而实现更加智能和个性化的服务。

3. 曼哈顿距离（Manhattan Distance）

概念：
曼哈顿距离是一种常用的距离度量方法，用于计算两个向量在各个维度上的绝对差值之和。它类似于在城市街区中沿着网格道路行走的距离，因此得名“曼哈顿距离”。这种距离度量方式特别适用于那些路径受限于网格结构的场景，如城市交通网络中的路径规划。

计算方法：
曼哈顿距离通过将两个向量在每个维度上的差的绝对值进行求和来计算。这种方法强调了各个特征之间的独立贡献，而不像欧氏距离那样考虑整体的几何距离。

公式：

举例：

• 文字分类：
  假设我们有两篇新闻报道 $A$ 和 $B$，它们的词频向量分别为 $A = (3, 0, 1, 2)$ 和 $B = (1, 2, 1, 1)$，表示在四个关键词上的出现次数。

  • 曼哈顿距离计算：

    $$|3 - 1| + |0 - 2| + |1 - 1| + |2 - 1| = 2 + 2 + 0 + 1 = 5$$

  • 解释：
    曼哈顿距离为5，表示两篇报道在关键词使用上的差异总和。距离越小，说明两篇报道在内容上的相似性越高，因为它们在各个关键词上的频率差异越小。

曼哈顿距离的优点与缺点

优点：

1. 简单直观：
   计算方法简单，只需将各个维度上的差的绝对值求和，易于理解和实现。

2. 适用于高维数据：
   在高维空间中，曼哈顿距离可以有效地衡量数据点之间的差异，特别适合特征之间相互独立的情况。

3. 对异常值不敏感：
   与欧氏距离相比，曼哈顿距离对单个维度上的异常值不那么敏感，因为它是各个维度差值的线性和。

缺点：

1. 忽略特征间的相关性：
   曼哈顿距离仅考虑各个特征的绝对差值，不考虑特征之间的相互关系，可能无法捕捉到数据中的复杂模式。

2. 不适合某些几何结构：
   在某些情况下，如数据点在连续空间中的分布，曼哈顿距离可能无法准确反映数据点之间的实际相似性。

应用场景

• 城市交通规划：
  曼哈顿距离用于计算城市中两点之间沿街道的实际行走距离，适用于网格化的道路系统。

• 文本分类与信息检索：
  在自然语言处理领域，通过计算文档的词频向量之间的曼哈顿距离，可以衡量文档内容的相似性，辅助分类和检索任务。

• 推荐系统：
  曼哈顿距离可用于衡量用户偏好向量与商品特征向量之间的差异，从而为用户推荐最符合其兴趣的商品。

总结

曼哈顿距离通过计算向量在各个维度上的绝对差值之和，提供了一种简单而有效的相似性度量方法。它在许多实际应用中表现出色，尤其适用于那些特征独立且路径受限于网格结构的场景。然而，曼哈顿距离也有其局限性，特别是在需要考虑特征间复杂关系的情况下。因此，在选择距离度量方法时，应根据具体的应用需求和数据特性来决定使用曼哈顿距离还是其他距离度量方法，如欧氏距离或余弦相似度。

示例回顾：

• 文字分类：
  两篇新闻报道 $A = (3, 0, 1, 2)$ 和 $B = (1, 2, 1, 1)$ 的曼哈顿距离为5，表示它们在四个关键词上的差异总和。距离越小，说明报道内容越相似。

通过理解和应用曼哈顿距离，我们能够在各种数据分析和机器学习任务中有效地衡量和发现数据之间的相似性，从而实现更加精准和智能的系统设计。

如何选择合适的相似性度量？

不同的相似性度量适用于不同的场景：

• 欧氏距离适合衡量总体差异，当向量的各个维度具有相同的量纲时效果较好。
• 余弦相似度适合关注方向而非大小的场景，常用于文本、文档和高维数据的相似性计算。
• 曼哈顿距离在维度较高时比欧氏距离更稳定，适合处理噪声数据和离群值。

举例说明选择：

• 文本搜索：在搜索引擎中，常用余弦相似度来比较用户的搜索词与网页内容的相似性，因为我们更关注文本的主题（方向）而非词频的绝对数量（大小）。
• 商品推荐：在电商平台上，根据用户的浏览和购买记录（转换为向量），可以使用欧氏距离或内积来找到与用户喜好相似的商品。

向量检索中的应用

在实际应用中，向量检索常用于：

• 图像搜索：根据一张图片找到相似的图片，例如以图搜图功能。
• 推荐系统：为用户推荐与其兴趣相似的物品，如电影、音乐、书籍等。
• 自然语言处理：比较文本、句子或词语的相似性，用于文本分类、情感分析等。
• 语义搜索：通过理解文本的含义（语义），找到与查询内容相关的文档。

实际案例：

• 语音助手：当你对语音助手说出一句话，它需要将你的语音转换为向量，与预先定义的指令向量进行比较，找到最匹配的指令执行。
• 社交媒体：根据用户发布的内容，分析文本和图片的特征，推荐可能感兴趣的好友或内容。

总结

相似性度量是向量检索的核心，通过数学方法衡量向量之间的相似程度。理解这些基本概念，不仅有助于我们更好地理解各种搜索、推荐系统和文本处理的原理，还能为深入学习人工智能和数据处理打下坚实的基础。

希望这篇文章能让你对向量相似性度量有一个清晰的认识！无论是图片、音乐还是文字，掌握了这些方法，都可以在数据的海洋中找到与你需求最匹配的信息。