while (left < right && a[keyi] >= a[left])
{
left++;
}
Swap(&a[left], &a[right]);
}
//交换(右边先走,能停在比key小的地方)
Swap(&a[keyi], &a[left]);
return left;
}
2️⃣ 挖坑法
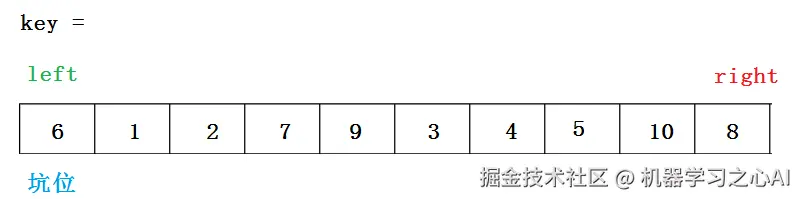
挖坑法 VS hoare版本
效率上来说:两者区别不大
挖坑法的优势是:更容易理解!(如果key取左边)很自然的就右边先走,找小,放到左边的坑里······hoare版本理解上更有难度
//挖坑法 int PartSort2(int* a, int left, int right) { int key = a[left]; int pit = left; while (left < right) { //找小 while (left < right && key <= a[right]) { right--; } a[pit] = a[right]; pit = right; //找大 while (left < right && key >= a[left]) { left++; } a[pit] = a[left]; pit = left; } a[pit] = key; return pit; }
3️⃣ 前后指针版本
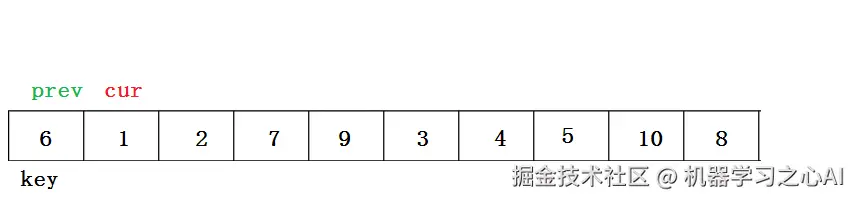
prev和cur之间间隔的值都比key大,所以prev和cur交换才能逐步把大的换到右侧,把小的换到左侧
//前后指针 //left int PartSort3(int* a, int left, int right) { int keyi = left; int cur = left + 1; int prev = left; while (cur <= right) { if (a[cur] < a[keyi] && a[++prev] != a[cur])//防止自己和自己交换 Swap(&a[cur], &a[prev]);
cur++;
}
Swap(&a[prev], &a[keyi]);
return prev;
}
##### 3.3.1 快速排序优化
1️⃣如果每次选出的key都是最小或最大的会使效率大大降低。例如:1 2 3 4 5 6 这种已经顺序了的,取最左或者最右都会很慢,于是我们想到能否选出一个不是最大也不是最小的数做key。
三数取中法选key
最左,最右,中间三个位置的数进行比较,选出中等大小的那个做key
//选出中等大小数的下标 int GetMidIndex(int* a, int left, int right) { int mid = left + (right - left) / 2;
if (a[left] < a[mid])
{
if (a[mid] < a[right])
{
return mid;
}
else if (a[left] < a[right])
{
return right;
}
else
{
return left;
}
}
else
{
if (a[right] > a[left])
{
return left;
}
else if (a[mid] > a[right])
{
return mid;
}
else
{
return right;
}
}
} int PartSort3(int* a, int left, int right) { //三数取中 int mid = GetMidIndex(a, left, right); Swap(&a[mid], &a[left]);
int keyi = left;
int cur = left + 1;
int prev = left;
while (cur <= right)
{
if (a[cur] < a[keyi] && a[++prev] != a[cur])//防止自己和自己交换
Swap(&a[cur], &a[prev]);
cur++;
}
Swap(&a[prev], &a[keyi]);
return prev;
}
2️⃣快排的结构是类似于二叉树的,二叉树最后几层的数是最多的,排序难度也很低,是否能够不递归到最小区间,中途就运用另一种排序方法返回有序数组给上一层来优化呢?当然是可以的
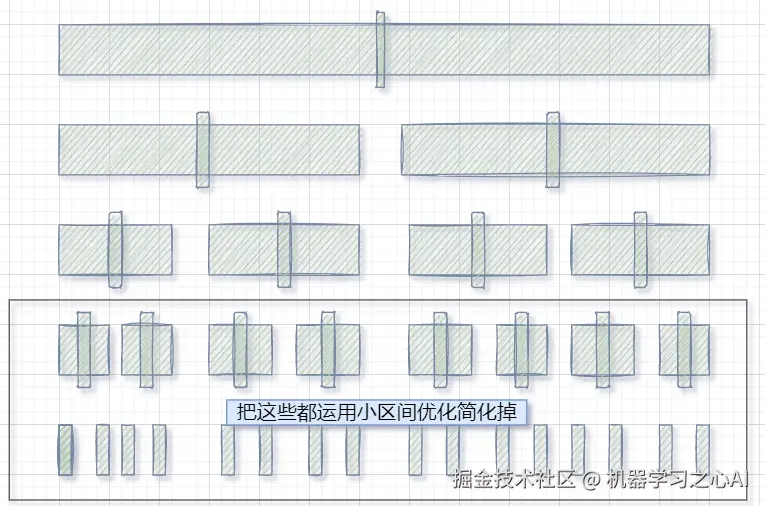
小区间优化: 递归到小的子区间时,可以考虑使用插入排序 ,减少递归调用
//加小区间优化 void QuickSort2(int* a, int begin, int end) { // 子区间相等只有一个值或者不存在那么就是递归结束的子问题 if (begin >= end) return;
if (end - begin + 1 <= 13)
{
InsertSort(a + begin, end - begin + 1);
}
else
{
int keyi = PartSort3(a, begin, end);
// [begin, keyi-1]keyi[keyi+1, end]
QuickSort2(a, begin, keyi - 1);
QuickSort2(a, keyi + 1, end);
}
}
##### 3.3.2 快速排序非递归
栈的代码可以到我之前的博文找 ,当然你如果会C++的话一切就更简单了。
//非递归 void QuickSort3(int* a, int begin, int end) { ST st; StackInit(&st); StackPush(&st, begin); StackPush(&st, end);
//右边处理完了再处理左边
while (!StackEmpty(&st))
{
int right = StackTop(&st);
StackPop(&st);
int left = StackTop(&st);
StackPop(&st);
int keyi = PartSort3(a, left, right);
//[left,keyi-1][keyi+1,right]
if (left < keyi - 1)
{
StackPush(&st, left);
StackPush(&st, keyi - 1);
}
if (keyi + 1 < right)
{
StackPush(&st, keyi + 1);
StackPush(&st, right);
}
}
StackDestory(&st);
}
>
> 快速排序的特性总结:
> 1️⃣ 快速排序整体的综合性能和使用场景都是比较好的,所以才敢叫快速排序
> 2️⃣ 时间复杂度:O(
>
>
>
>
> N
>
>
> ∗
>
>
> l
>
>
> o
>
>
> g
>
>
> N
>
>
>
> N\*logN
>
>
> N∗logN)
>
>
> 3️⃣ 空间复杂度:O(
>
>
>
>
> l
>
>
> o
>
>
> g
>
>
> N
>
>
>
> logN
>
>
> logN)~O(
>
>
>
>
> N
>
>
>
> N
>
>
> N)(最坏情况每次key都取到最大或最小,要递归n层)
>
>
> 4️⃣ 稳定性:不稳定(选key,三数取中,很多因素使它不稳定)
>
>
>
## 4. 7️⃣归并排序
基本思想:
归并排序(MERGE-SORT)是建立在归并操作上的一种有效的排序算法,该算法是采用分治法(Divide andConquer)的一个非常典型的应用。将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为二路归并。 (有微积分那味了)

//有点像前序遍历 void _MergeSort(int* a, int begin, int end, int* tmp) { //停止条件——只有一个的时候 if (begin >= end) return;
int mid = begin + (end - begin) / 2;
//区间的分割要小心,可能会出现死循环
//[begin,mid][mid+1,end]
\_MergeSort(a, begin, mid, tmp);
\_MergeSort(a, mid + 1, end, tmp);
//归并
//printf("[%d, %d][%d, %d]\n", begin, mid, mid + 1, end);
int begin1 = begin, end1 = mid;
int begin2 = mid + 1, end2 = end;
int index = begin;
while (begin1 <= end1 && begin2 <= end2)
{
if (a[begin1] < a[begin2])
{
tmp[index++] = a[begin1++];
}
else
{
tmp[index++] = a[begin2++];
}
}
while (begin1 <= end1)
{
tmp[index++] = a[begin1++];
}
while (begin2 <= end2)
{
tmp[index++] = a[begin2++];
}
//拷回去
memcpy(a + begin, tmp + begin, (end - begin + 1) \* sizeof(int));
}
void MergeSort(int* a, int n) { int* tmp = (int*)malloc(sizeof(int) * n); assert(tmp);
\_MergeSort(a, 0, n - 1, tmp);
free(tmp);
}
### 4.1 归并排序非递归

边界处理永远的泪😭
//非递归 void MergeSortR(int* a, int n) { int* tmp = (int*)malloc(sizeof(int) * n); assert(tmp); int gap = 1;
while (gap < n)
{
//间距为gap为一组,两两归并
for (int i = 0; i < n; i += 2 \* gap)
{
int begin1 = i, end1 = i + gap - 1;
int begin2 = i + gap, end2 = i + 2 \* gap - 1;
//只有end1越界,直接修正
if (end1 >= n)
end1 = n - 1;
//begin2不存在,第二个区间不存在,修正成一个不存在的区间
if (begin2 >= n)
{
begin2 = n;
end2 = n - 1;
}
//begin2没事end2越界,修正end2
if (end2 >= n)
end2 = n - 1;
int index = i;
//printf("[%d, %d][%d, %d]\n", begin1, end1, begin2, end2);
while (begin1 <= end1 && begin2 <= end2)
{
if (a[begin1] < a[begin2])
{
tmp[index++] = a[begin1++];
}
else
{
tmp[index++] = a[begin2++];
}
}
while (begin1 <= end1)
{
tmp[index++] = a[begin1++];
}
while (begin2 <= end2)
{
tmp[index++] = a[begin2++];
}
}
memcpy(a, tmp, n \* sizeof(int));
gap \*= 2;
}
free(tmp);
}
>
> 归并排序的特性总结:
> 1️⃣ 归并的缺点在于需要O(N)的空间复杂度,归并排序的思考更多的是解决在磁盘中的**外排序问题**。
> 2️⃣ 时间复杂度:O(N\*logN)
> 3️⃣ 空间复杂度:O(N)
>
>
> 4️⃣ 稳定性:稳定
>
>
>
## 5. 非比较排序
### 5.1 8️⃣计数排序

思想:计数排序又称为鸽巢原理,是对哈希直接定址法的变形应用。 操作步骤:
1. 统计相同元素出现次数
2. 根据统计的结果将序列回收到原来的序列中
//适用于范围集中的数,排负数也行 void CountSort(int* a, int n) { int min = a[0], max = a[0]; for (int i = 1; i < n; i++) { if (a[i] > max) max = a[i]; if (a[i] < min) min = a[i]; } int range = max - min + 1; int* countA = (int*)calloc(range, sizeof(int)); assert(countA);
for (int i = 0; i < n; i++)
{
countA[a[i] - min]++;
}
int j = 0;
for (int i = 0; i < range; i++)
{
while (countA[i]--)
{
a[j++] = i + min;
}
}
}
>
> 计数排序的特性总结:
> 1️⃣ 计数排序在数据范围集中时,效率很高,但是适用范围及场景有限,浮点数就没法排。
> 2️⃣ 时间复杂度:O(MAX(N,范围))
> 3️⃣ 空间复杂度:O(范围)
>
>
> 4️⃣ 稳定性:稳定
>
>
>
### 5.2 9️⃣桶排序
桶排序是计数排序的升级版。它利用了函数的映射关系,高效与否的关键就在于这个映射函数的确定。桶排序 (Bucket sort)的工作的原理:假设输入数据服从均匀分布,将数据分到有限数量的桶里,每个桶再分别排序(有可能再使用别的排序算法或是以递归方式继续使用桶排序进行排)。
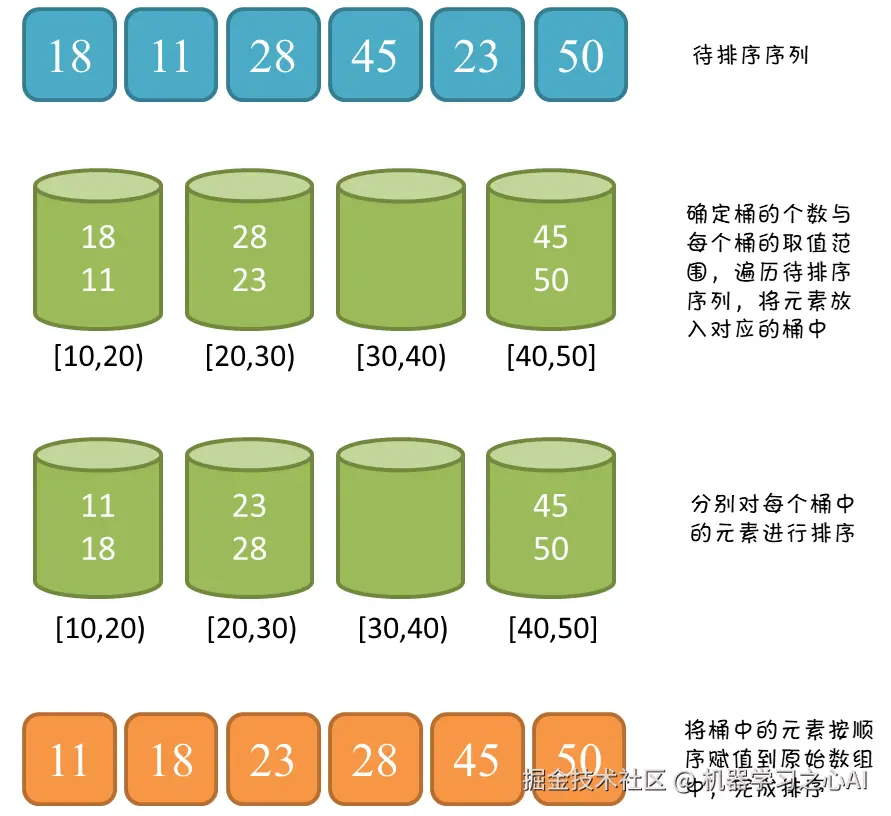
操作步骤:
1. 设置一个定量的数组当作空桶;
2. 每个桶存放该区间的数据,由于每个桶内的数据元素个数不确定,可以使用**链表**表示,同时使用插入排序,让每个桶的链表有序。
3. 这样按照次序将所有桶的元素连起来就得到完整的有序列表。
typedef int SLTDataType; typedef struct SListNode { SLTDataType data; struct SListNode* next; }SListNode;
void InsertNode(SListNode** bucket, int data) { SListNode* p = (SListNode*)malloc(sizeof(SListNode)); p->data = data; p->next = NULL;
// 桶为空
if (\*bucket == NULL)
{
\*bucket = p;
}
else
{
SListNode\* prev = NULL;
SListNode\* cur = \*bucket;
while (cur != NULL && cur->data <= data)
{
prev = cur;
cur = cur->next;
}
// 对插入到第一个结点前的情况处理
if (prev == NULL)
{
\*bucket = p;
p->next = cur;
}
else
{
prev->next = p;
p->next = cur;
}
}
}
void BucketSort(int* arr, int n) { //寻找最大值最小值 int max = arr[0], min = arr[0]; for (int x = 0; x < n; x++) { max = arr[x] > max ? arr[x] : max; min = arr[x] < min ? arr[x] : min; }
//获取容量
int bucketsize = (max - min) / n + 1;
//获取桶数量
int bucketcount = (max - min) / bucketsize + 1;
//申请桶空间
SListNode\*\* b=(SListNode\*\*)calloc(bucketcount, sizeof(SListNode\*));
//分配数据
for (int i = 0; i < n; i++)
{
//算出arr[i]对应的桶位置
int pos = (arr[i] - min) / bucketsize;
InsertNode(&b[pos], arr[i]);
}
//将数据返回到数组
SListNode\* tmp;
for (int i = 0, j = 0; i < bucketcount && j < n; i++)
{
if (b[i] != NULL)
{
tmp = b[i];
while (tmp != NULL)
{
arr[j++] = tmp->data;
tmp = tmp->next;
}
}
}
//free
for (int i = 0; i < bucketcount; i++)
{
while (b[i] != NULL)
{
tmp = b[i];
b[i] = tmp->next;
free(tmp);
}
}
free(b);
}
>
> 桶排序的特性总结:
>
>
> 1️⃣时间复杂度:O(range + N)
>
>
> 2️⃣空间复杂度:O(range + N)
>
>
> 3️⃣稳定性:稳定。
>
>
>
### 5.3 🔟基数排序
基数排序是按照低位先排序,然后收集;再按照高位排序,然后再收集;依次类推,直到最高位。有时候有些属性是有优先级顺序的,先按低优先级排序,再按高优先级排序。最后的次序就是高优先级高的在前,高优先级相同的低优先级高的在前。

//求最大位数 int Maxbit(int* arr, int n) { int max = arr[0]; for (int i = 1; i < n; i++) { if (arr[i] > max) max = arr[i]; }
int k = 1;
while (max >= 10)
{
max /= 10;
k++;
}
return k;
}
void RadixSort(int* arr, int n) { int k = Maxbit(arr, n); int radix = 1; int* tmp = (int*)malloc(sizeof(int) * n);
while (k)
{
int bucket[10] = { 0 };
//统计每个桶的数据个数
for (int i = 0; i < n; i++)
{
bucket[arr[i] / radix % 10]++;
}
//累加
for (int i = 1; i < 10; i++)
{
bucket[i] += bucket[i - 1];
}
//向tmp数组存入数据
for (int i = n - 1; i >= 0; i--)
{
tmp[bucket[arr[i] / radix % 10] - 1] = arr[i];
bucket[arr[i] / radix % 10]--;
}
//将tmp序列拷贝到原数组中
memcpy(arr, tmp, n \* sizeof(int));
radix \*= 10;
k--;
}
free(tmp);
}
>
> 基数排序的特性总结:
>
>
> 1️⃣时间复杂度:O(range \* N)
>
>
> 2️⃣空间复杂度:O(range + N)
>
>
> 3️⃣稳定性:稳定。
>
>
>
## 总结:排序算法复杂度及稳定性分析
| 排序方式 | 时间复杂度(平均) | 时间复杂度(最坏) | 时间复杂度(最好) | 空间复杂度 | 稳定性 |
| --- | --- | --- | --- | --- | --- |
| 直接插入排序 | O(
n
2
n^2
n2) | O(
n
2
n^2
n2) | O(
n
n
n) | O(
1
1
1) | 稳定 |
| 希尔排序 | O(
n
l
o
g
n
nlogn
nlogn)~ O(
n
2
n^2
n2) | O(
n
2
n^2
n2) | O(
n
1.3
n^{1.3}
n1.3) | O(
1
1
1) | 不稳定 |
| 直接选择排序 | O(
n
2
n^2
n2) | O(
n
2
n^2
n2) | O(
n
2
n^2
n2) | O(
1
1
1) | 不稳定 |
| 堆排序 | O(
n
l
o
g
2
n
nlog\_2n
nlog2n) | O(
n
l
o
g
2
n
nlog\_2n
nlog2n) | O(
n
l
o
g
2
n
nlog\_2n
nlog2n) | O(
1
1
1) | 不稳定 |
| 冒泡排序 | O(
n
2
n^2
n2) | O(
n
2
n^2
n2) | O(
n
n
n) | O(
1
1
1) | 稳定 |
| 快速排序 | O(
n
l
o
g
2
n
nlog\_2n
nlog2n) | O(
n
2
n^2
n2) | O(
n
l
o
g
2
n
nlog\_2n
nlog2n) | O(
l
o
g
2
n
log\_2n
log2n)~O(
n
n
n) | 不稳定 |
| 归并排序 | O(
n
l
o
g
2
n
nlog\_2n
nlog2n) | O(
n
l
o
g
2
n
nlog\_2n
nlog2n) | O(
n
l
o
g
2
n
nlog\_2n
nlog2n) | O(
n
n
n) | 稳定 |
| 计数排序 | O(
n
+
k
n+k
n+k) | O(
n
+
k
n+k
n+k) | O(
n
+
k
n+k
n+k) | O(
n
+
k
n+k
n+k) | 稳定 |
| 桶排序 | O(
n
+
k
n+k
n+k) | O(
n
2
n^2
n2) | O(
n
n
n) | O(
n
+
k
n+k
n+k) | 稳定 |
| 基数排序 | O(
n
∗
k
n\*k
n∗k) | O(
n
∗
k
n\*k
n∗k) | O(
n

**网上学习资料一大堆,但如果学到的知识不成体系,遇到问题时只是浅尝辄止,不再深入研究,那么很难做到真正的技术提升。**
**[需要这份系统化的资料的朋友,可以添加戳这里获取](https://gitee.com/vip204888)**
**一个人可以走的很快,但一群人才能走的更远!不论你是正从事IT行业的老鸟或是对IT行业感兴趣的新人,都欢迎加入我们的的圈子(技术交流、学习资源、职场吐槽、大厂内推、面试辅导),让我们一起学习成长!**