浅解四元数

白金大神
214 阅读3分钟

写在前面

本文只涉及到了解四元数的基本信息，不涉及四元数原理，且下文知识适用于unity开发

正文

定义

  • 四元数是一个四维复数，由一个实轴(w)和三个虚轴(i, j, k)组成
    q=w+xi+yj+zk q = w + xi + yj + zk
    代入旋转角度θ\theta则公式为：
    q=cos(θ/2)+sin(θ/2)(xi+yj+zk) q = cos(\theta /2) + sin(\theta /2)(xi + yj + zk)
    这里：
    • x, y, z是向量部分，表示旋转轴的方向，且这个向量必须是单位向量，sin(θ/2)sin(\theta /2)是向量的长度
    • w是标量部分，代表旋转角度一半的余弦值，也就是cos(θ/2)cos(\theta/2)
    • i, j, k是虚数单位，数学计算的抽象概念，它们满足以下关系
      i2=j2=k2=ijk=1ij=kjk=iki=jji=−kkj=−iik=−j i^2 = j^2 = k^2 = ijk = 1 \\ \begin{align} ij &= k &\quad jk &= i &\quad ki &= j \\ ji &= -k &\quad kj &= -i &\quad ik &= -j \end{align}

基本运算

这里先对四元数的基本运算有个粗略的认知，以便于更好的理解下文内容

  • 加法

    q1+q2=(w1+x1∗i+y1∗j+z1∗k)+(w2+x2∗i+y2∗j+z2∗k)=+(w1+w2)+(x1+x2)i+(y1+y2)j+(z1+z2)k \begin{align} q_1 + q_2 &= (w_1 + x_1*i + y_1*j + z_1*k) + (w_2 + x_2*i + y_2*j + z_2*k) \\ &= + (w_1 + w_2) + (x_1 + x_2)i + (y_1 + y_2)j + (z_1 + z_2)k \end{align}

    四元数的加法就是每个轴系数相加

  • 乘法

    • 系数乘法

      λq=λw+λx+λy+λz \lambda q = \lambda w + \lambda x + \lambda y + \lambda z

    • 四元数乘法

      q1q2=(w1+x1∗i+y1∗j+z1∗k)∗(w2+x2∗i+y2∗j+z2∗k)=(w1w2−x1x2−y1y2−z1z2)+i(w1x2+w2x1+y1z2−y2z1)+j(w1y2+w2y1+z1x2−z2x1)+k(w1z2+w2z1+x1y2−x2y1)=[w1w2−v1⋅v2, w1v2+w2v1+v2×v1]\begin{align} q_1 q_2 &= (w_1 + x_1*i + y_1*j + z_1*k ) * (w_2 + x_2*i + y_2*j + z_2*k) \\ &= (w_1 w_2 - x_1 x_2 - y_1 y_2 - z_1 z_2) \\ &+ i(w_1 x_2 + w_2 x_1 + y_1 z_2 - y_2 z_1) \\ &+ j(w_1 y_2 + w_2 y_1 + z_1 x_2 - z_2 x_1) \\ &+ k(w_1 z_2 + w_2 z_1 + x_1 y_2 - x_2 y_1) \\ &= [w_1 w_2 - v_1·v_2,\ w_1 v_2 + w_2 v_1 + v_2 \times v_1] \end{align}

      [注] 这里v1⋅v2v_1 · v_2是向量点乘，v1×v2v_1 \times v_2是叉乘，且四元数的乘法不满足交换律

      四元数的乘法就是多项式相乘，一个多项式的各项去乘另一个多项式的每一项，最后再加起来，上文中最后的表达式时经过整理简化的，方便套公式

  • 四元数的共轭

    q∗=[w, −xi, −yj, −zk] q^* = [w,\ -xi,\ -yj,\ -zk]

    实数不变，虚数取负

  • 四元数的逆

    q∗q−1=1q−1=q∗/∣q∣2 \begin{align} q^* q^{-1} &= 1 \\ q^{-1} &= q^* / |q|^2 \end{align}
    (q1q2)−1=q2−1q1−1 (q_1 q_2)^{-1} = q_2^{-1} q_1^{-1} \\

四元数如何表示旋转

  • 四元数与欧拉角的转换

    • 绕x轴旋转α\alpha

      qx=sinα2i+cosα2 q_x = sin \frac{\alpha}{2} i + cos \frac{\alpha}{2}

    • 绕y轴旋转α\alpha

      qy=sinα2j+cosα2 q_y = sin \frac{\alpha}{2} j + cos \frac{\alpha}{2}

    • 绕z轴旋转α\alpha

      qz=sinα2k+cosα2 q_z = sin \frac{\alpha}{2} k + cos \frac{\alpha}{2}

      在将一个欧拉角转换为四元数时，需要将xyz的旋转组合起来，四元数使用左乘的方式，按照unity欧拉角zxy的旋转顺序对于到四元数表示为q=qzqxqyq = q_z q_x q_y

    • 举例：将欧拉角 (60,60,60) 转换成四元数

      q=qzqxqy=(cos(602)+sin(602)i)∗(cos(602)+sin(602)j)∗(cos(602)+sin(602)k)=(32+12i)∗(32+12j)∗(32+12k)=(34+34j+34i−14k)∗(32+12k)=33+18+3+38i+3−38j+3−38k=0.7745+0.5915i+0.1584j+0.1584k\begin{align} q &= q_z q_x q_y \\ &= (cos(\frac{60}{2}) + sin(\frac{60}{2})i) * (cos(\frac{60}{2}) + sin(\frac{60}{2})j) * (cos(\frac{60}{2}) + sin(\frac{60}{2})k) \\ &= (\frac{\sqrt{3}}{2} + \frac{1}{2} i) * (\frac{\sqrt{3}}{2} + \frac{1}{2} j) * (\frac{\sqrt{3}}{2} + \frac{1}{2} k) \\ &= (\frac{3}{4} + \frac{\sqrt{3}}{4} j + \frac{\sqrt{3}}{4} i - \frac{1}{4} k)*(\frac{\sqrt{3}}{2} + \frac{1}{2}k) \\ &= \frac{3 \sqrt{3} + 1}{8} + \frac{3 + \sqrt{3}}{8} i + \frac{3 - \sqrt{3}}{8} j + \frac{3 - \sqrt{3}}{8} k \\ &= 0.7745 + 0.5915 i + 0.1584 j + 0.1584 k \end{align}

      即欧拉角 (60,60,60) 对应的四元数为 (0.5915, 0.1584, 0.1584, 0.7745)，unity表示的四元数w为最后一位

  • 四元数乘法应用旋转

    • 绕任意向量旋转，设对应旋转的四元数是q，需要左乘q再右乘q的共轭，有公式：

      v′=qv^q∗ v' = q\hat{v}q*

      如果你想知道四元数旋转的原理，推荐去看这篇文章：zhuanlan.zhihu.com/p/636543643

    • 举例：对于向量 v(1,3,4) 绕着向量 u(1,1,1) 旋转60度，得到新的向量v'，首先对 u 单位化：(13,13,13)(\frac{1}{\sqrt{3}}, \frac{1}{\sqrt{3}}, \frac{1}{\sqrt{3}})

      qrot=cosθ2+usinθ2=cosθ2+xsinθ2i+ysinθ2j+zsinθ2k=cosπ6+13sinπ6i+13sinπ6j+13sinπ6k=32+123i+123j+123kqv=0+i+3j+4kqrot∗=32−123i−123j−123k \begin{align} &\begin{align} q_{rot} &= cos\frac{\theta}{2} + u sin\frac{\theta}{2} \\ &= cos\frac{\theta}{2} + x sin\frac{\theta}{2} i + y sin\frac{\theta}{2} j + z sin\frac{\theta}{2} k \\ &= cos\frac{\pi}{6} + \frac{1}{\sqrt{3}} sin\frac{\pi}{6} i + \frac{1}{\sqrt{3}} sin\frac{\pi}{6} j + \frac{1}{\sqrt{3}} sin\frac{\pi}{6} k \\ &= \frac{\sqrt{3}}{2} + \frac{1}{2\sqrt{3}} i + \frac{1}{2\sqrt{3}} j + \frac{1}{2\sqrt{3}} k \\ \end{align} \\ &q_v = 0 + i + 3j + 4k \\ &q_{rot}^* = \frac{\sqrt{3}}{2} - \frac{1}{2\sqrt{3}} i - \frac{1}{2\sqrt{3}} j - \frac{1}{2\sqrt{3}} k \\ \end{align}
      • 首先计算qrotqvq_{rot}q_v
        qrotqv=(32+123i+123j+123k)∗(0+i+3j+4k)=−43+23i+3j+73k\begin{align} q_{rot}q_v &= (\frac{\sqrt{3}}{2} + \frac{1}{2\sqrt{3}} i + \frac{1}{2\sqrt{3}} j + \frac{1}{2\sqrt{3}} k) * (0 + i + 3j + 4k) \\ &= -\frac{4}{\sqrt{3}} + \frac{2}{\sqrt{3}} i + \sqrt{3} j + \frac{7}{\sqrt{3}} k \end{align}
      • 计算qrotqvqrot∗q_{rot}q_vq_{rot}^*
        qrotqvqrot∗=(−43+23i+3j+73k)∗(32−123i−123j−123k)=0+76i+43j+133k\begin{align} q_{rot}q_vq_{rot}^* &= ( -\frac{4}{\sqrt{3}} + \frac{2}{\sqrt{3}} i + \sqrt{3} j + \frac{7}{\sqrt{3}} k) * (\frac{\sqrt{3}}{2} - \frac{1}{2\sqrt{3}} i - \frac{1}{2\sqrt{3}} j - \frac{1}{2\sqrt{3}} k) \\ &= 0 + \frac{7}{6} i + \frac{4}{3} j + \frac{13}{3}k \end{align}

  • 在unity中使用四元数

    Vector3 axisPoint = new Vector3(1,1,1); // 旋转轴
float angle = 60.0f; // 旋转角度
Vector3 point = new Vector3(1, 3, 4); // 旋转点

Quaternion rotation = Quaternion.AngleAxis(angle, axisPoint.normalized); // 获取旋转四元数
Quaternion inverseRotation = Quaternion.Inverse(rotation); // 获取旋转四元数的共轭

Vector3 newPoint; // 定义旋转后的点

// 第一种方法 直接将四元数视为旋转变换应用于向量
newPoint = rotation * point;

// 第二种方法，使用四元数乘法
Quaternion resultQuaterion = rotation * new Quaternion(point.x, point.y, point.z, 0) * inverseRotation;
newPoint.x = resultQuaterion.x;
newPoint.y = resultQuaterion.y;
newPoint.z = resultQuaterion.z;

    unity中，Quaternion * Vector3 实际上是将四元数视为一个旋转矩阵, 而不是传统的四元数左乘右乘形式

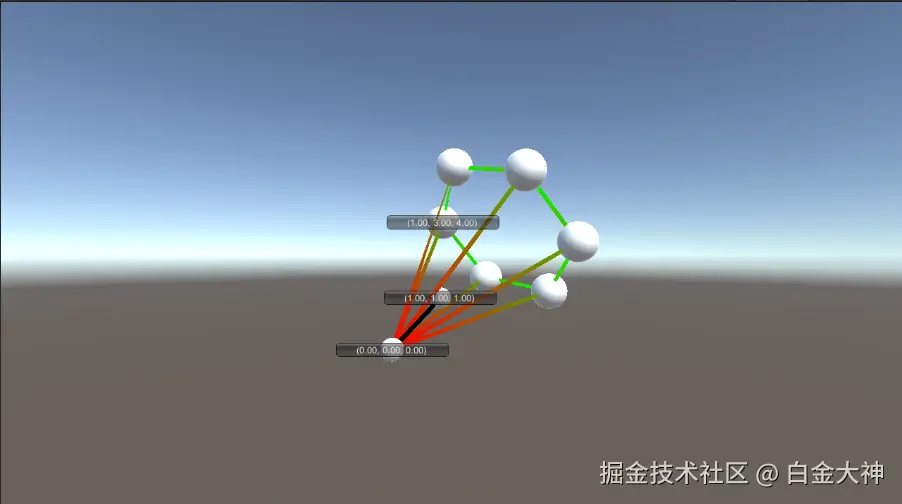
最后附上向量 v(1,3,4)  绕着向量 u(1,1,1)  旋转60度6次的展示图

四元数旋转.png

四元数旋转2.png

avatar
文章
阅读
粉丝