SM3密码算法学习笔记

SM3密码算法是中国自主研发的一种密码哈希算法，具有高效、安全和可控的特点。它广泛应用于数字签名、消息认证码、随机数生成等密码学应用中，并且与国际上广泛使用的SHA-256等哈希算法相比，SM3算法具有更高的安全性和可控性。

1.概述

输入：$0<L<2^{64}$

输出：$256bit$ 的消息摘要

对长度为L比特的消息m，SM3杂凑算法经过填充和迭代压缩，生成杂凑值，杂凑值长度为256比特。

2.填充

填充消息也就是进行补位操作，第一位补1，其余位补k个0，直到满足$l+1+k \equiv 448 \ mod \ 512$。

一个消息填充的示例如下图：

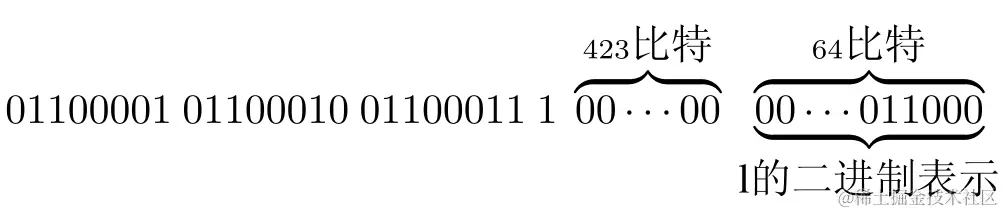
3.迭代压缩

常数与函数

初始值

$IV=7380166f \ 4914b2b9 \ 172442d7 \ da8a0600 \ a96f30bc \ 163138aa \ e38dee4d \ b0fb0e4e$

常量

${T_j} = \begin{cases} 79cc4519, & \qquad 0 \le t \le 15 \\ 7a879d8a, & \qquad 16 \le t \le 63 \end{cases}$

布尔函数

${FF_j(X,Y,Z)} = \begin{cases} X \oplus Y \oplus Z, & \qquad 0 \le t \le 15 \\ (X \land Y) \lor (X\land Z) \lor (Y\land Z), & \qquad 16 \le t \le 63 \end{cases}$

${GG_j(X,Y,Z)} = \begin{cases} X \oplus Y \oplus Z, & \qquad 0 \le t \le 15 \\ (X \land Y) \lor (\lnot X\land Z), & \qquad 16 \le t \le 63 \end{cases}$

式中X，Y，Z为字。

置换函数

$P_0{(X)}=X \oplus (X<<<9) \oplus (X<<<17)$

$P_1{(X)}=X \oplus (X<<<15) \oplus (X<<<23)$

式中X为字。

3.1 迭代过程

将填充后的消息$m^′$分成512-bit的信息块，可以表示为$m^′=B^{(0)}B^{(1)}...B^{(n-1)}$

其中$n=(l+k+65)/512$

对$m^′$进行n次迭代，$V^{(i+1)}=CF(V^{(i)},B^{(i)})$，其中$CF$为压缩函数，$V^{(0)}$为256比特初始值$IV$，$B^{(i)}$为填充后的消息分组，迭代压缩的结果为$V^{(n)}$。

3.2 消息扩展

将消息分组$B^{(i)}$按如下方法扩展生成132个字$W_0,W_1,...,W_{67},W^′_0,W^′_1,...,W^′_{63}$，用于压缩函数$CF$

a) 将消息分组$B^{(i)}$划分为16个字$W_0,W_1,...,W_{15}$

b) 对于$W_{16}-W_{67}$，

$W_j \gets P_1(W_{j-16} \oplus W_{j-9} \oplus (W_{j-3}<<<15)) \oplus (W_{j-13}<<<7) \oplus W_{j-6}$

c) 对于$W^′_{0}-W^′_{63}$，

$W^′_j=W_j \oplus W_{j+4}$

3.3 压缩函数

令A、B、C、D、E、F、G、H为字寄存器，SS1、SS2、TT1、TT2为中间变量，压缩函数$V^{(i+1)}=CF(V^{(i)},B^{(i)})，0 \le i \le n-1$。计算过程描述如下

$ABCDEFG \gets V^{(i)}$

执行64次运算

$SS1 \gets ((A<<<12)+E+(T_j<<<j))<<<7$

$SS2 \gets SS1 \oplus (A<<<12)$

$TT1 \gets FF_j(A,B,C)+D+SS2+W^′_j$

$TT2 \gets GG_j(E,F,G)+H+SS1+W_j$

$D \gets C$

$C \gets B <<< 9$

$B \gets A$

$A \gets TT1$

$H \gets G$

$G \gets F <<< 19$

$F \gets E$

$E \gets P_0(TT2)$

执行这些运算后，执行

$V^{(i+1)} \gets ABCDEFG \oplus V^{(i)}$

其中，字的存储为大端（big-endian）格式。

杂凑值

$ABCDEFG \gets V^{(n)}$

输出256比特的杂凑值$y=ABCDEFGH$