杂凑函数之SHA-1学习笔记

算法简介

SHA1（Secure Hash Algorithm 1，安全散列算法1）是一种密码散列函数，由美国国家安全局（NSA）设计，并由美国国家标准与技术研究院（NIST）发布为联邦信息处理标准（FIPS）的出版物之一。SHA1算法能够产生一个160位（20字节）的散列值，通常表示为40个十六进制字符。

算法详解

输入：$0<L<2^{64}$

输出：160bit的消息摘要

SHA-1算法的主要流程如下图所示：

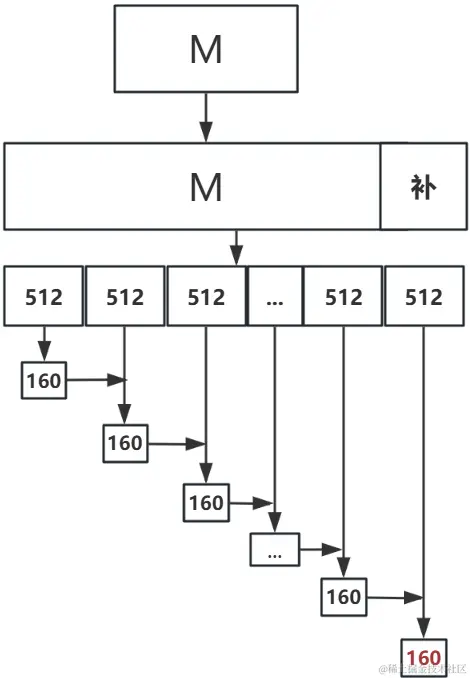
一. 预处理

1.消息填充

填充消息也就是进行补位操作，第一位补1，其余位补足够的0，直到满足$L \ mod \ 512 = 448$。

这里有一个问题，那就是为什么要补这个数量的0呢？答案就是剩余的$512-448=64$位，要存储消息的长度。

一个消息填充的示例如下图：

2.填充消息解析

将填充后的消息分成 N 个512-bit的信息块，可以表示为$M^{(1)}$，$M^{(2)}$，...，$M^{(N)}$。因为512bits的信息块可以表示为16个32-bitz字，所以第i个信息块可以表示为$M^{(i)}_0$，$M^{(i)}_1$，...，$M^{(i)}_{15}$。

3.设置初始哈希值

初始哈希值$H^{(0)}$由以下五个32-bit字组成。

$H^{(0)}_0=67452301$

$H^{(0)}_1=efcdab89$

$H^{(0)}_2=98badcfe$

$H^{(0)}_3=10325476$

$H^{(0)}_4=c3d2e1f0$

二.计算

预处理完成后，每个消息块$M^{(1)}$，$M^{(2)}$，...，$M^{(N)}$按照以下顺序进行处理。

1.准备消息表

准备消息表${W_t}$

${W_t} = \begin{cases} M^{(i)}_t, & \qquad 0 \le t \le 15 \\ ROTL^1{(W_{t-3} \oplus W_{t-8} \oplus W_{t-14} \oplus W_{t-16})}, & \qquad 16 \le t \le 79 \end{cases}$

其中$ROTL$为左移位运算。

2.初始化工作变量

初始化$a,b,c,d,e$五个工作变量

$a=H^{(i-1)}_0$

$b=H^{(i-1)}_1$

$c=H^{(i-1)}_2$

$d=H^{(i-1)}_3$

$e=H^{(i-1)}_4$

3.执行80轮运算

由准备消息表中可知，t的数值范围为0到79，则根据t的数值，进行80轮运算，每轮运算执行以下计算:

$T=ROTL^5{(a)}+f_t{(b,c,d)}+e+K_t+W_t$

$e=d$

$d=c$

$c=ROTL^{30}{(b)}$

$b=a$

$a=T$

其中涉及的有关运算如下：

$K_t= \begin{cases} 5a827999 & \qquad 0 \le t \le 19 \\ 6ed9eba1 & \qquad 20 \le t \le 39 \\ 8f1bbcdc & \qquad 40 \le t \le 59 \\ ca62c1d6 & \qquad 60 \le t \le 79 \end{cases}$

$f_t{(x,y,z)}= \begin{cases} Ch(x,y,z)=(x \land y) \oplus (\sim x \land z) & \qquad 0 \le t \le 19 \\ Parity(x,y,z)=x \oplus y \oplus z & \qquad 20 \le t \le 39 \\ Maj(x,y,z)=(x \land y) \oplus (x \land z) \oplus (y \land z) & \qquad 40 \le t \le 59 \\ Parity(x,y,z)=x \oplus y \oplus z & \qquad 20 \le t \le 39 \end{cases}$

4.计算中间哈希值

计算中间哈希值$H^{(i)}$

$H^{(i)}_0=a+H^{(i-1)}_0$

$H^{(i)}_1=b+H^{(i-1)}_1$

$H^{(i)}_2=c+H^{(i-1)}_2$

$H^{(i)}_3=d+H^{(i-1)}_3$

$H^{(i)}_4=e+H^{(i-1)}_4$

三.最终结果

在重复进行上述计算过程N次后，消息M的160-bit消息摘要为

$H^{(N)}_0 \parallel H^{(N)}_1 \parallel H^{(N)}_2 \parallel H^{(N)}_3 \parallel H^{(N)}_4$

参考资料

参考文档：Secure Hash Standard