数组是计算机科学中最基础的数据结构之一。它具有固定大小、元素类型一致,并且通过索引可以快速访问。本文将详细介绍数组的定义、基本操作(包括插入和删除),并提供相关的动态图演示,帮助你更直观地理解这些操作。
一、数组的基本概念
定义
数组就像是一排储物柜,每个储物柜都有一个唯一的编号(索引),你可以通过这个编号快速找到并访问储物柜中的物品(元素)。数组是具有相同类型数据元素的有序集合。
特性
- 固定大小:数组在创建时必须指定大小,一旦创建,大小就不能改变。这就像是一排固定数量的储物柜,你不能轻易增加或减少储物柜的数量。
- 元素类型一致:数组中的所有元素必须是相同的数据类型。就像储物柜只能用来存放同一类型的物品。
- 索引访问:数组中的每个元素都有一个唯一的索引,通过索引可以快速访问元素。
二、数组的基本操作
创建数组
在不同的编程语言中,数组的初始化和声明方式有所不同。就像在不同的国家,储物柜的设计和使用方式可能不同。
Java示例:
int[] arr = new int[5]; // 创建一个大小为5的整数数组
Python示例:
arr = [0] * 5 # 创建一个包含5个0的列表(数组)
JavaScript示例:
let arr = new Array(5); // 创建一个大小为5的数组
访问元素
通过索引可以快速访问数组中的元素。索引从0开始,指向第一个元素。就像通过储物柜的编号,可以快速找到并打开指定的储物柜。
Java示例:
int firstElement = arr[0]; // 访问第一个元素
Python示例:
first_element = arr[0] # 访问第一个元素
JavaScript示例:
let firstElement = arr[0]; // 访问第一个元素
修改元素
可以通过索引修改数组中的元素。就像通过储物柜的编号找到指定的储物柜,并将其中的物品替换成新的物品。
Java示例:
arr[0] = 10; // 将第一个元素的值修改为10
Python示例:
arr[0] = 10 # 将第一个元素的值修改为10
JavaScript示例:
arr[0] = 10; // 将第一个元素的值修改为10
三、数组的插入和删除操作
插入操作
在数组的特定位置插入元素时,需要将该位置及其后的所有元素向后移动一位,以腾出空间插入新元素。这个操作的时间复杂度为 O(n),其中 n 是数组的长度。就像在中间插入一个储物柜,需要把后面的储物柜都向后移动一个位置。
Java示例:
public void insertElement(int[] arr, int index, int element) {
for (int i = arr.length - 1; i > index; i--) {
arr[i] = arr[i - 1];
}
arr[index] = element;
}
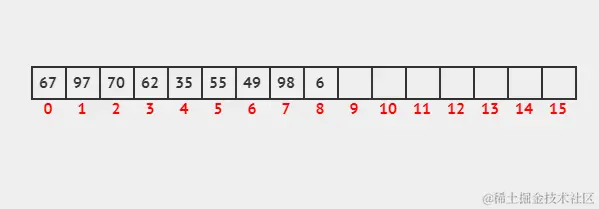
插入操作的动态图演示
在i = 5处插入数字55
删除操作
在数组的特定位置删除元素时,需要将该位置后的所有元素向前移动一位,以填补被删除元素的位置。这个操作的时间复杂度为 O(n),其中 n 是数组的长度。就像删除中间的一个储物柜,需要把后面的储物柜都向前移动一个位置。
Java示例:
public void deleteElement(int[] arr, int index) {
for (int i = index; i < arr.length - 1; i++) {
arr[i] = arr[i + 1];
}
arr[arr.length - 1] = 0; // 或者 arr = Arrays.copyOf(arr, arr.length - 1);
}
删除操作的动态图演示
[数组删除操作演示]
Java ArrayList 源码分析:增加和删除操作
Java 的 ArrayList 是一个动态数组,它可以在需要时自动调整大小。与普通数组相比,ArrayList 提供了更灵活的操作,如动态添加和删除元素。下面我们来详细分析 ArrayList 的源码,了解其增删操作的实现。
ArrayList 增加操作
源码解析
在 ArrayList 中,增加元素的方法主要有两种:在末尾添加和在指定位置插入。我们首先来看在末尾添加元素的方法 add(E e):
public boolean add(E e) {
ensureCapacityInternal(size + 1); // 检查并扩容
elementData[size++] = e; // 将元素添加到数组末尾
return true;
}
关键方法解析
- ensureCapacityInternal(int minCapacity):
- 该方法检查当前数组是否有足够的容量,如果没有,则扩展数组容量。
private void ensureCapacityInternal(int minCapacity) {
if (elementData == DEFAULTCAPACITY_EMPTY_ELEMENTDATA) {
minCapacity = Math.max(DEFAULT_CAPACITY, minCapacity);
}
ensureExplicitCapacity(minCapacity);
}
private void ensureExplicitCapacity(int minCapacity) {
modCount++;
// overflow-conscious code
if (minCapacity - elementData.length > 0)
grow(minCapacity);
}
- grow(int minCapacity):
- 该方法负责实际扩容操作,通常是将数组大小增加到当前大小的 1.5 倍。
private void grow(int minCapacity) {
// overflow-conscious code
int oldCapacity = elementData.length;
int newCapacity = oldCapacity + (oldCapacity >> 1); // 增加 50%
if (newCapacity - minCapacity < 0)
newCapacity = minCapacity;
if (newCapacity - MAX_ARRAY_SIZE > 0)
newCapacity = hugeCapacity(minCapacity);
// minCapacity is usually close to size, so this is a win:
elementData = Arrays.copyOf(elementData, newCapacity);
}
在指定位置插入元素
下面我们来看在指定位置插入元素的方法 add(int index, E element):
public void add(int index, E element) {
rangeCheckForAdd(index); // 检查索引范围
ensureCapacityInternal(size + 1); // 检查并扩容
System.arraycopy(elementData, index, elementData, index + 1, size - index); // 移动元素
elementData[index] = element; // 插入元素
size++;
}
关键方法解析
- rangeCheckForAdd(int index):
- 该方法检查插入索引是否在有效范围内。
private void rangeCheckForAdd(int index) {
if (index > size || index < 0)
throw new IndexOutOfBoundsException(outOfBoundsMsg(index));
}
- System.arraycopy:
- 该方法用于将指定数组中的数据复制到另一数组。这里用于移动原有元素以腾出插入位置。
ArrayList 删除操作
源码解析
在 ArrayList 中,删除元素的方法有两种:按索引删除和按对象删除。我们来看按索引删除的方法 remove(int index):
public E remove(int index) {
rangeCheck(index); // 检查索引范围
modCount++;
E oldValue = elementData(index); // 获取被删除的元素
int numMoved = size - index - 1;
if (numMoved > 0)
System.arraycopy(elementData, index + 1, elementData, index, numMoved); // 移动元素
elementData[--size] = null; // 释放最后一个元素
return oldValue;
}
关键方法解析
- rangeCheck(int index):
- 该方法检查删除索引是否在有效范围内。
private void rangeCheck(int index) {
if (index >= size)
throw new IndexOutOfBoundsException(outOfBoundsMsg(index));
}
- elementData(int index):
- 该方法用于获取指定索引处的元素。
E elementData(int index) {
return (E) elementData[index];
}
按对象删除元素
下面我们来看按对象删除的方法 remove(Object o):
public boolean remove(Object o)
{
if (o == null) {
for (int index = 0; index < size; index++)
if (elementData[index] == null) {
fastRemove(index);
return true;
}
} else {
for (int index = 0; index < size; index++)
if (o.equals(elementData[index])) {
fastRemove(index);
return true;
}
}
return false;
}
关键方法解析
- fastRemove(int index):
- 该方法用于快速删除指定索引处的元素。
private void fastRemove(int index) {
modCount++;
int numMoved = size - index - 1;
if (numMoved > 0)
System.arraycopy(elementData, index + 1, elementData, index, numMoved);
elementData[--size] = null; // clear to let GC do its work
}
总结
通过对 ArrayList 源码的分析,我们可以看到其增加和删除操作的实现细节。ArrayList 通过动态扩容机制确保有足够的空间存储元素,同时通过 System.arraycopy 方法高效地移动元素以实现插入和删除操作。
-
增加操作:
add(E e): 在末尾添加元素,时间复杂度为 O(1)(均摊)。add(int index, E element): 在指定位置插入元素,时间复杂度为 O(n)。
-
删除操作:
remove(int index): 按索引删除元素,时间复杂度为 O(n)。remove(Object o): 按对象删除元素,时间复杂度为 O(n)。
通过这些操作的源码分析,我们可以深入理解 ArrayList 的工作机制,并在实际开发中更好地利用和优化 ArrayList。
四、数组的优缺点
优点
- 快速随机访问:数组支持通过索引快速访问任意元素,时间复杂度为 O(1)。
- 内存连续:数组在内存中是连续存储的,利用了 CPU 缓存,访问速度较快。
缺点
- 大小固定:数组在创建时必须指定大小,无法动态调整,可能导致内存浪费或溢出。
- 插入和删除操作成本高:在数组中间插入或删除元素时,需要移动大量元素,时间复杂度为 O(n)。
五、典型应用场景
使用场景
- 需要快速访问元素的场景:由于数组支持 O(1) 时间复杂度的随机访问,适合用于需要频繁访问元素的场景,如图像处理中的像素数组。
- 静态数据存储:当数据集大小固定且不需要频繁插入或删除时,数组是一个高效的选择,如配置参数列表。
数组操作的时间复杂度详解
在计算机科学中,时间复杂度是衡量算法效率的一个重要指标。它描述了算法在输入规模变化时,执行时间如何增长。在处理数组时,不同的操作有不同的时间复杂度。以下是对数组常见操作的时间复杂度的详细解释:
1. 创建数组
创建一个数组时,计算机需要在内存中分配一块连续的空间以存储数组的元素。这个操作的时间复杂度为 O(1),因为分配内存的时间通常是常数时间,不依赖于数组的大小。
示例(Java):
int[] arr = new int[100]; // 创建一个大小为100的整数数组
2. 访问元素
数组支持通过索引访问任意元素,访问的时间复杂度为 O(1)。这是因为数组在内存中是连续存储的,可以通过元素的索引直接计算出其内存地址。
示例(Java):
int firstElement = arr[0]; // 访问第一个元素
3. 修改元素
通过索引修改数组中的元素,时间复杂度也是 O(1),因为和访问元素一样,修改元素只需通过索引直接定位到对应的内存地址,然后进行修改。
示例(Java):
arr[0] = 10; // 将第一个元素的值修改为10
4. 插入元素
4.1 在数组末尾插入元素
在数组末尾插入元素是最简单的情况,只需要将新元素放在数组的最后一个位置即可,时间复杂度为 O(1)。
示例(Java):
arr[arr.length - 1] = 99; // 在数组末尾插入元素
4.2 在数组中间插入元素
在数组中间插入元素时,需要将插入位置后的所有元素向后移动一位,以腾出空间插入新元素。这个操作的时间复杂度为 O(n),其中 n 是数组的长度。在最坏情况下,需要移动所有元素。
示例(Java):
public void insertElement(int[] arr, int index, int element) {
for (int i = arr.length - 1; i > index; i--) {
arr[i] = arr[i - 1];
}
arr[index] = element;
}
5. 删除元素
5.1 删除数组末尾的元素
删除数组末尾的元素只需要简单地减少数组的大小或忽略最后一个元素,时间复杂度为 O(1)。
示例(Java):
arr[arr.length - 1] = 0; // 删除数组末尾的元素
5.2 删除数组中间的元素
在数组中间删除元素时,需要将删除位置后的所有元素向前移动一位,以填补被删除元素的位置。这个操作的时间复杂度为 O(n),其中 n 是数组的长度。在最坏情况下,需要移动所有元素。
示例(Java):
public void deleteElement(int[] arr, int index) {
for (int i = index; i < arr.length - 1; i++) {
arr[i] = arr[i + 1];
}
arr[arr.length - 1] = 0;
}
6. 搜索元素
6.1 线性搜索
线性搜索是最基本的搜索方法,从数组的第一个元素开始,依次检查每个元素,直到找到目标元素或遍历完整个数组。时间复杂度为 O(n),其中 n 是数组的长度。
示例(Java):
public int linearSearch(int[] arr, int target) {
for (int i = 0; i < arr.length; i++) {
if (arr[i] == target) {
return i;
}
}
return -1; // 未找到目标元素
}
6.2 二分搜索
二分搜索是一种高效的搜索方法,适用于已排序的数组。它通过反复将搜索范围减半,快速定位目标元素。时间复杂度为 O(log n),其中 n 是数组的长度。
示例(Java):
public int binarySearch(int[] arr, int target) {
int left = 0;
int right = arr.length - 1;
while (left <= right) {
int mid = left + (right - left) / 2;
if (arr[mid] == target) {
return mid;
} else if (arr[mid] < target) {
left = mid + 1;
} else {
right = mid - 1;
}
}
return -1; // 未找到目标元素
}
总结
| 操作类型 | 时间复杂度 | 说明 |
|---|---|---|
| 创建数组 | O(1) | 内存分配是常数时间 |
| 访问元素 | O(1) | 通过索引直接访问 |
| 修改元素 | O(1) | 通过索引直接修改 |
| 插入元素(末尾) | O(1) | 直接在末尾插入 |
| 插入元素(中间) | O(n) | 需要移动元素 |
| 删除元素(末尾) | O(1) | 直接删除末尾元素 |
| 删除元素(中间) | O(n) | 需要移动元素 |
| 线性搜索 | O(n) | 逐个检查元素 |
| 二分搜索 | O(log n) | 适用于已排序数组 |
通过了解数组不同操作的时间复杂度,可以更好地选择适当的数据结构和算法,提高程序的效率。在实际开发中,应根据具体需求和场景选择合适的操作方式和数据结构。希望本文对你理解数组操作的时间复杂度有所帮助。如果你有任何问题或进一步的探讨,欢迎在评论区留言讨论。
参考资料:
- 《算法导论》 - Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, Clifford Stein
- Java Documentation
- VisuAlgo
感谢阅读!如果觉得有帮助,请点赞、分享,并关注更多精彩内容。