为什么需要双线性插值算法？

ChatGP回答： 双线性插值（bilinear interpolation）是一种常用的插值方法，用于在二维空间内估算未知点的值。它主要应用于图像处理、计算机视觉、地理信息系统（GIS）、数值分析和其他需要在二维数据中进行平滑过渡的领域。

白话解释： 在二维图像数据中，它的坐标都是整数，例如：$(1,1),(52,53)$这种，但是如果在某种算法计算中，需要获取 $(50.5,100.3)$ 类似这种坐标的像素值，常规就两种思路：

1、最近取值。这里就是直接取 $(50, 100)$​的像素值

2、邻近插值。这里就是利用 $(50, 100),(51, 100),(50, 101),(51, 101)$ 这几个坐标像素值的组合

上述的第二种思路： 其实就是双线性插值。

在本章节中，主要解决的问题就是： 大区域应用低分辨率纹理，避免过于离谱的马赛克（像素风）效果！

如下图： 左图就是最近邻取值，右图就是双线性插值！

双线性插值算法是什么？

已知图像的四个位置的像素值，$f(x_0, y_0) = v0, \quad f(x_1, y_0) = v1, \quad f(x_0, y_1) = v2, \quad f(x_01, y_1) = v3$

计算$f(x, y) = ? \quad (x_0 < x < x_1 \quad且\quad y_0 < y < y_1)$

如何双线性插值？

问题描述： 已知直线起始端点 $p_0 = (x_0, y_0)$ ， $p_1 = (x_1, y_1)$，$f(p_0) = v_0$ ，$f(p_1) = v_1$，求直线上任意一点 $p=(x,y)$，$f(p) = ?$

如下图所示：

双线性插值指两次线性插值： 可以先插值x再插值y，也可以先插值y再插值x。咱们这里先x，再y。

1、连接 $(x_0, y_0)和(x_1,y_0)$ ， $(x_0, y_1)和(x_1,y_1)$， 将$(x,y)$ 投影到两条两条直线上，交点分别为：$(x,y_0)和(x,y_1)$

如下图所示：

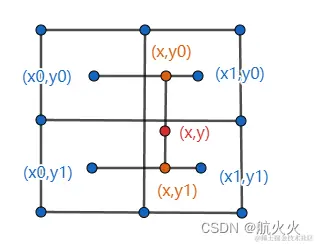
咱们分别计算：$f(x, y_0)和f(x,y_1)$

这里的思路就不用解释了吧，前面文章关于直线线性插值已经讲过了，不懂的小伙伴可以回去翻翻哦！

2、通过 $f(x,y_0)和f(x,y_1)$​ 的值，再做一次插值得到$f(x,y)$

大功告成，是不是很简单呢！

结尾：喜欢的小伙伴可以点点关注+赞哦

希望对各位小伙伴能够有所帮助哦，永远在学习的道路上伴你而行， 我是航火火，火一般的男人！