【洛谷】P1049 装箱问题

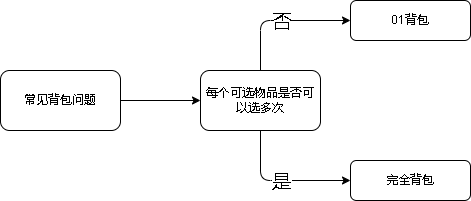
确认所需算法

题目链接：P1049 装箱问题

这题是一道背包问题，如果你还不知道什么是背包问题，那么请看我这篇文章

既然我们知道了这道题是一道背包问题，那么下一步我们要确认他是01背包还是完全背包。

首先我们回顾01背包和完全背包的区别：

通过题意可知，每种物品有且只有一个，所以这题是01背包。

思路

区别

这题是相对裸的01背包，只有以下两点不同：

1. 物品价值=物品体积
2. 输出的是剩余体积，不是被占用的体积

状态转移方程

每种物品只有装/不装两种：

1. 如果装，那么价值就是f[j - w[i]] + w[i]，注意这里我使用w[i]代表第i个物品的价值/体积。
2. 如果不装，那么价值就是f[j]

代码

#include<cstdio>
#include<stack>
#include<iostream>
using namespace std;
int w[100],n,v,f[30000]; 
int main(){
    cin >> v >> n;
    for (int i = 1;i <= n;++i) cin >> w[i]; 
    for(int i=1;i<=n;i++){
        for(int j=v;j>=w[i];j--){ 
            f[j]=max(f[j],f[j-w[i]]+w[i]); 
        }
    }
    cout << v - f[v]; 
    return 0;
}

本文使用 文章同步助手 同步