hello,我是爱记笔记的doing。这次学习背包问题,特此记录。
关于背包问题的经典资料自然是著名的“背包九讲”,如果需要猛戳这里获取。
但是背包九讲对于我们蒟蒻来说实在不友好,只有伪代码,十分不方便,所以才有了这篇笔记。
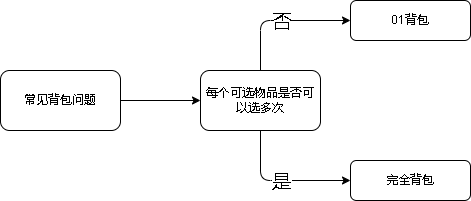
首先我们需要了解——常见的背包问题类型有哪些?有什么区别?为了方便大家理解,可以看这幅图。
01背包
什么是01背包
01背包的原型就是指一个最大体积容量为V的背包,N个物品,第i个物品的体积是w[i],价值为v[i],求将物品装入背包最大的价值是多少。
理解01背包
这就是标准的01背包问题。那么如何理解它呢?我们首先思考:f[i]代表的是什么?在一般的01背包中,f[i]代表的是当背包大小为i时的最大价值。先看代码:
#include<iostream>
using namespace std;
int vv,n,w[110],v[110],f[10100];
int main(){
cin >> vv >> n;
for (int i = 1;i <= n;++i) cin >> w[i] >> v[i];
for (int i = 1;i <= n;++i){
for (int j = vv;j >= w[i];--j){
f[j] = max(f[j],f[j - w[i]] + v[i]);
}
}
cout << f[vv];
return 0;
}
这时有人就会问了:为什么j要反着来?这要从01背包和完全背包说起。
01背包每个物品不可以选多次,假设容量是10,物品体积是2,如果正着来:
| 背包容量 | 选的个数 |
|---|---|
| 0 | 0 |
| 1 | 0 |
| 2 | 1 |
| 3 | 1 |
| 4 | 2 |
| 5 | 2 |
| 6 | 3 |
| 7 | 3 |
| 8 | 4 |
| 9 | 4 |
| 10 | 5 |
发现问题了吗?物品被选了多次!为什么呢?因为每次推算后边的都会根据前边的推算,如果计算完了f[2],那么计算f[4]时发现还可以装一个,那么数量就是1+1=2!所以,如果从后往前推算,计算到f[4]时,发现f[2]=0,每次状态转移方程只会将物品数量增加1,那么便可以实现每个物品只选一次!反之,如果将循环正过来,那就成了完全背包!
完全背包
上一段已经将01和完全背包代码的区别讲的很清楚了,那么这一段就直接贴代码:
#include<iostream>
using namespace std;
int vv,n,w[110],v[110],f[10100];
int main(){
cin >> vv >> n;
for (int i = 1;i <= n;++i) cin >> w[i] >> v[i];
for (int i = 1;i <= n;++i){
for (int j = w[i];j <= vv;++j){
f[j] = max(f[j],f[j - w[i]] + v[i]);
}
}
cout << f[vv];
return 0;
}
本文使用 文章同步助手 同步