平衡二叉树(AVL)

概念：

1. 它的左右子树都是AVL树。
2. 左右子树高度之差(简称平衡因子)的绝对值不超过1。
3. 空树也是AVL树。

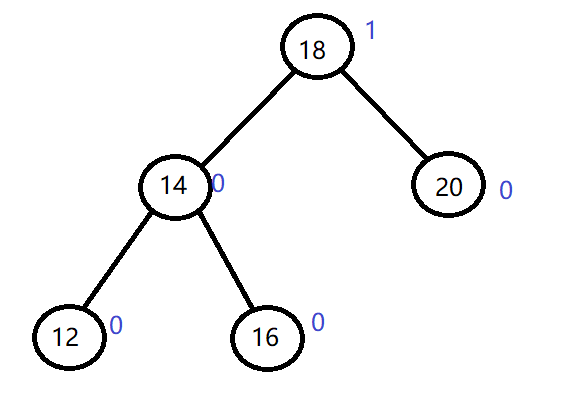
定义节点：

用三叉链实现。要频繁使用到当前元素的父节点。

template <class K>
struct AVLTreeNode
{
    AVLTreeNode<K>* _left;
    AVLTreeNode<K>* _right;
    AVLTreeNode<K>* _parent;
    int _balance;
    K _key;

    AVLTreeNode(const K& key)
        :_left(nullptr)
         ,_right(nullptr)
         ,_parent(nullptr)
         ,_balance(0)
         ,_key(key)
    {}
};

定义树：

template <class K>
class AVLTree
{
    typedef AVLTreeNode<K> Node;
 public:
    // 增删查等成员函数
 private:
    Node* _root = nullptr;
}

插入

严格保证log(N)的高度，是需要旋转的。

插入的数据有可能影响局部子树，也有可能往上不断影响，因此有可能对局部或者更深一层进行旋转处理。

最重要的评判依据便是平衡因子：平衡因子 = 左子树高度 - 右子树高度。

1. 新增节点的平衡因子是0。
2. parent->_balance = 0，说明插入之前parent是一边高一边低，左高右低往右插入或者左低右高往左插入，此时还是平衡的。
3. parent->_balance = 1 or -1，说明插入之前parent是左右相等，要么插入左边要么插入右边。
4. parent->_balance = 2 or -2，说明插入之前是parent一边高一边低，插入的位置还是高的那边，此时就需要旋转。

插入的过程中，如果往根的左边插入，那么根的平衡因子++，如果往根的右边插入，那么根的平衡因子--。

更新平衡因子代码

while(parent)
{
    // 插入到左子树
    if(cur == parent->_left)
    {
        parent->_balance++;
    }
    // 插入到右子树
    else
    {
        parent->_balance--;
    }

    // 说明未插入时平衡因子是0
    if(parent->_balance == 1 || parent->_balance == -1)
    {
   		// 此时parent是平衡的，但parent的平衡因子增加可能会导致自己父亲的平衡因子为2，要往上调整
        parent = parent->_parent;
        cur = cur->_parent;
    }
    else if(parent->_balance == 2 || parent->_balance == -2)
    {
        // 要旋转
        if(parent->_balance == 2 && cur->_balance == 1)
        {
            // 左边高右边低 --- 右旋转
            RotateR(parent);
            break;
        }
        else if(parent->_balance == -1 && cur->_balance == -1)
        {
            // 右边高左边低 --- 左旋转
            RotateL(parent);
            break;
        }
        else if(parent->_balance == 2 && cur->_balance == -1)
        {
            // 左右双旋
            RotateLR(parent);
            break;
        }
        else if(parent->_balance == -2 && cur->_balance == 1)
        {
            // 右左双旋
            RotateRL(parent);
            break;
        }
    }
    else
    {
        // 插入后平衡因子为0，说明之前一边高一边低，在低的那边插入了。也不影响父亲的父亲的平衡因子
        break;
    }
    return true;
}

单旋

1. 找到失衡的根节点。
2. 将失衡的节点的左孩子的右孩子交给该节点的左孩子。
3. 将该节点交给该节点的左孩子的右孩子。
4. 这样旋转的目的是依旧让该树为二叉搜索树。

抽象图：

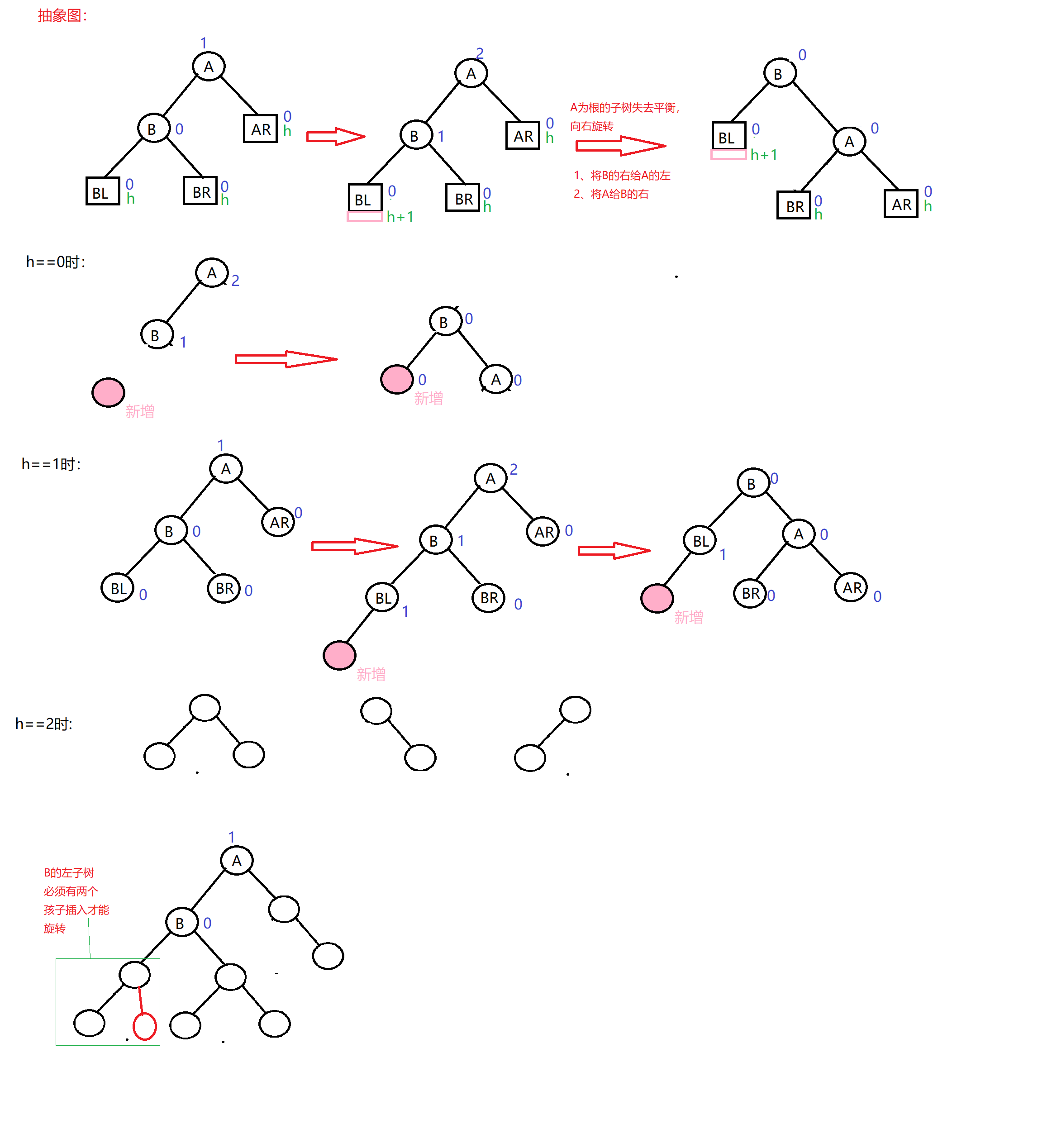
左旋和右旋代码：

右旋

void RotateR(Node* parent)
{
    Node* leftNode = parent->_left;
    Node* rightNode = leftNode->_right;

    parent->_left = rightNode;
    if(rightNode)
        rightNode->_parent = parent;

    // 保存parent的父节点
    Node* node = parent->_parent;
    leftNode->_right = parent;
    parent->_parent = leftNode;

    // node有可能是空，根节点没父亲
    if(node == nullptr)
    {
        _root = leftNode;
        leftNode->_parent = nullptr;
    }
    else
    {
        if(node->_left == parent)
        {
            node->_left = leftNode;
        }
        else
        {
            node->_right = leftNode;
        }

        leftNode->_parent = node;
    }

    // 单旋之后的平衡因子都是0
    parent->_balance = leftNode->_balance = 0;
}

左旋

void RotateL(Node* parent)
{
    Node* rightNode = parent->_right;
    Node* leftNode = rightNode->_left;

    parent->_right = leftNode;
    if(leftNode)
        leftNode->_parent = parent;

    Node* node = parent->_parent;
    rightNode->_left = parent;
    parent->_parent = rightNode;

    if(node == nullptr)
    {
        _root = rightNode;
        rightNode->_parent = nullptr;
    }
    else
    {
        if(node->_left == parent)
        {
            node->_left = rightNode;
        }
        else
        {
            node->_right = rightNode;
        }

        rightNode->_parent = node;
    }

    parent->_balance = rightNode->_balance = 0;
}

双旋

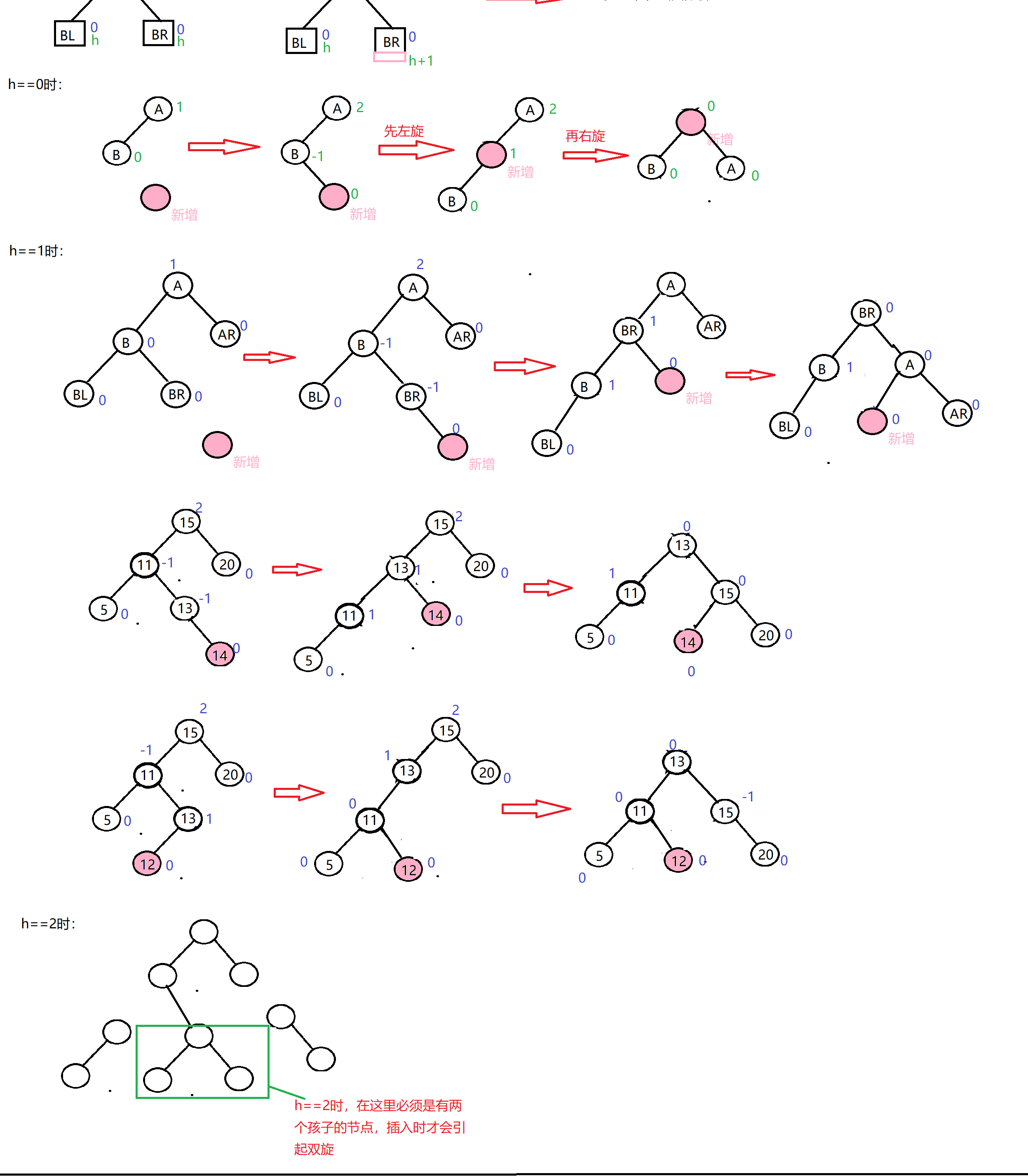
左右双旋代码：

需要注意的是：在左旋过程中，插入的位置不同，最后的平衡因子也不同，要对插入的位置进行分析。

void RotateLR(Node* parent)
{
    // 插入的位置不同最后的平衡因子不同
    // 先保存之前的
    Node* leftNode = parent->_left;
    Node* rightNode = leftNode->_right;
    int balance = rightNode->_balance;

    RotateL(parent->_left);
    RotateR(parent);

    // 右子树新增
    if(balance == -1)
    {
        parent->_balance = 0;
        rightNode->_balance = 0;
        leftNode->_balance = 1;
    }
    // 左子树新增
    else if(balance == 1)
    {
        leftNode->_balance = 0;
        rightNode->_balance = 0;
        parent->_balance = -1;
    }
    else
    {
        leftNode->_balance = 0;
        rightNode->_balance = 0;
        parent->_balance = 0;
    }
}

放个右左双旋的例子：

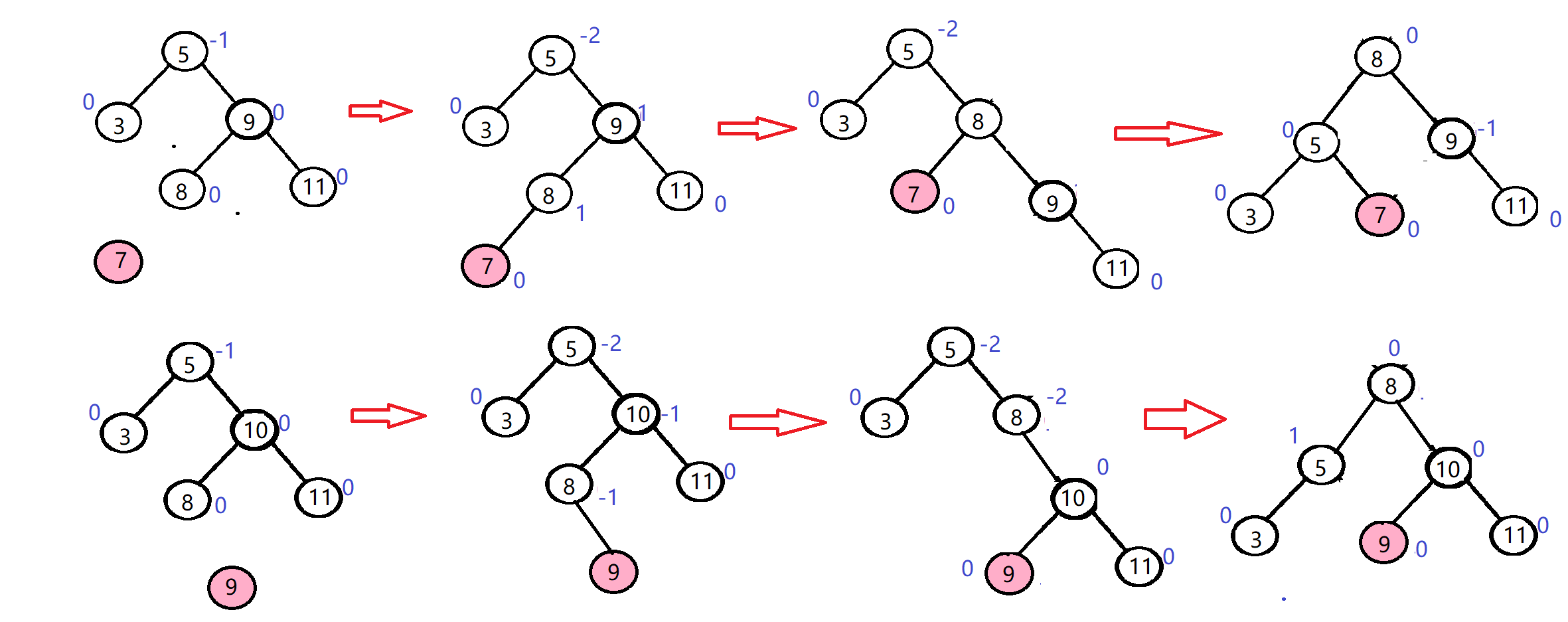
右左双旋代码：

void RotateRL(Node* parent)
{
    Node* rightNode = parent->_right;
    Node* leftNode = rightNode->_left;
    int balance = leftNode->_balance;

    RotateR(parent->_right);
    RotateL(parent);

    // 左子树新增
    if(balance == 1)
    {
        parent->_balance = 0;
        leftNode->_balance = 0;
        rightNode->_balance = -1;
    }
    // 右子树新增
    else if(balance == -1)
    {
        parent->_balance = 1;
        rightNode->_balance = 0;
        leftNode->_balance = 0;
    }
    // 左子树新增
    else
    {
        parent->_balance = 0;
        leftNode->_balance = 0;
        rightNode->_balance = 0;
    }
}

---

示例

判断该树是否是AVL树？

1. 一个方面是要看是否是二叉搜索树，也就是中序遍历是否有序。
2. 还要看插入的过程中每个节点的平衡因子是否大于1或者小于-1。

满足以上两条才算是AVL树。

判断节点的平衡因子代码：

bool IsBalance()
{
    return _IsBalance(_root);
}

int _Height(Node* root)
{
    if(root == nullptr)
    {
        return 0;
    }

    int leftH = _Height(root->_left);
    int rightH = _Height(root->_right);
    return leftH > rightH ? leftH + 1 : rightH + 1;
}

bool _IsBalance(Node* root)
{
    if(root == nullptr)
    {
        return true;
    }

    int leftH = _Height(root->_left);
    int rightH = _Height(root->_right);

    return abs(leftH - rightH) < 2
        && _IsBalance(root->_left)
        && _IsBalance(root->_right);
}

主函数：

#include "AVLTree.hpp"

int main()
{
    int a[] = {5, 3, 9, 8, 11};
    AVLTree<int> t;
    for(auto ch : a)
    {
        t.Insert(ch);
        cout << ch << " 插入: " << t.IsBalance() << endl;
    }
    t.MidOrder();
    t.Insert(7);
    t.MidOrder();
    return 0;
}

查找

类似二叉搜索树的查找。。

删除

~~有时间在写。