二叉搜索树

the_day
102 阅读5分钟

二叉搜索树

二叉搜索树又称二叉排序树，它或者是一棵空树，或者是具有以下性质的二叉树:

若它的左子树不为空，则左子树上所有节点的值都小于根节点的值

若它的右子树不为空，则右子树上所有节点的值都大于根节点的值

它的左右子树也分别为二叉搜索树

image-20240318111011226

  • 定义节点

    template<class K>
struct BSTreeNode
{
    BSTreeNode<K>* _left;
    BSTreeNode<K>* _right;
    K _key;

    BSTreeNode(const K& key)
        :_left(nullptr)
         ,_right(nullptr)
         ,_key(key)
    {}
};

  • 定义二叉搜索树

    template <class K>
class BSTree
{
    typedef BSTreeNode<K> Node;
public:
    // 增删改查等成员函数
private:
    Node* _root = nullptr;
}

增加

  1. 从根节点开始进行比较。
  2. 如果比根节点值大，就插入到根节点的右子树中。
  3. 如果比根节点值小，就插入到根节点的左子树中。
  4. 如果插入的值已经存在，就返回。
  5. 重复2、3步，直到找到插入的位置。

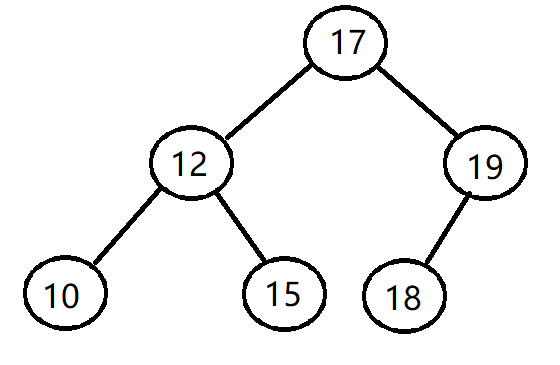
比如插入16：

image-20240318113112204

代码实现:

 bool Insert(const K& key)
 {
    if(_root == nullptr)
    {
        _root = new Node(key);
        return true;
    }

    // 新增节点要和父节点进行连接，要知道父节点
    Node* parent = nullptr;
    Node* cur = _root;
    while(cur)
    {
        // 如果当前节点大于插入的节点，就往左边插入
        if(cur->_key > key)
        {
            parent = cur;
            cur = cur->_left;
        }
        // 如果当前节点小于插入的节点，就往右边插入
        else if(cur->_key < key)
        {
            parent  = cur;
            cur = cur->_right;
        }
        // 如果当前节点等于要插入的节点，就返回
        else
        {
            return false;
        }
    }

    // 这里就是找到了要插入节点的位置
   cur = new Node(key);
   // 判断是插入parent的左边还是右边
   if(parent->_key > key)
   {
       parent->_left = cur;
   }
   else
   {
        parent->_right = cur;
   }

   return true;
}

查找

和插入一样的步骤。

代码实现:

bool Find(const K& key)
{
    Node* cur = _root;
    while(cur)
    {
        if(cur->_key < key)
        {
            cur = cur->_right;
        }
        else if(cur->_key > key)
        {
            cur = cur->_left;
        }
        else
        {
            return true;
        }
    }

    return false;
}

删除

一共的删除情况:

  1. 删除的节点没有孩子。
  2. 删除的节点有一个孩子。
  3. 删除的节点有两个孩子。

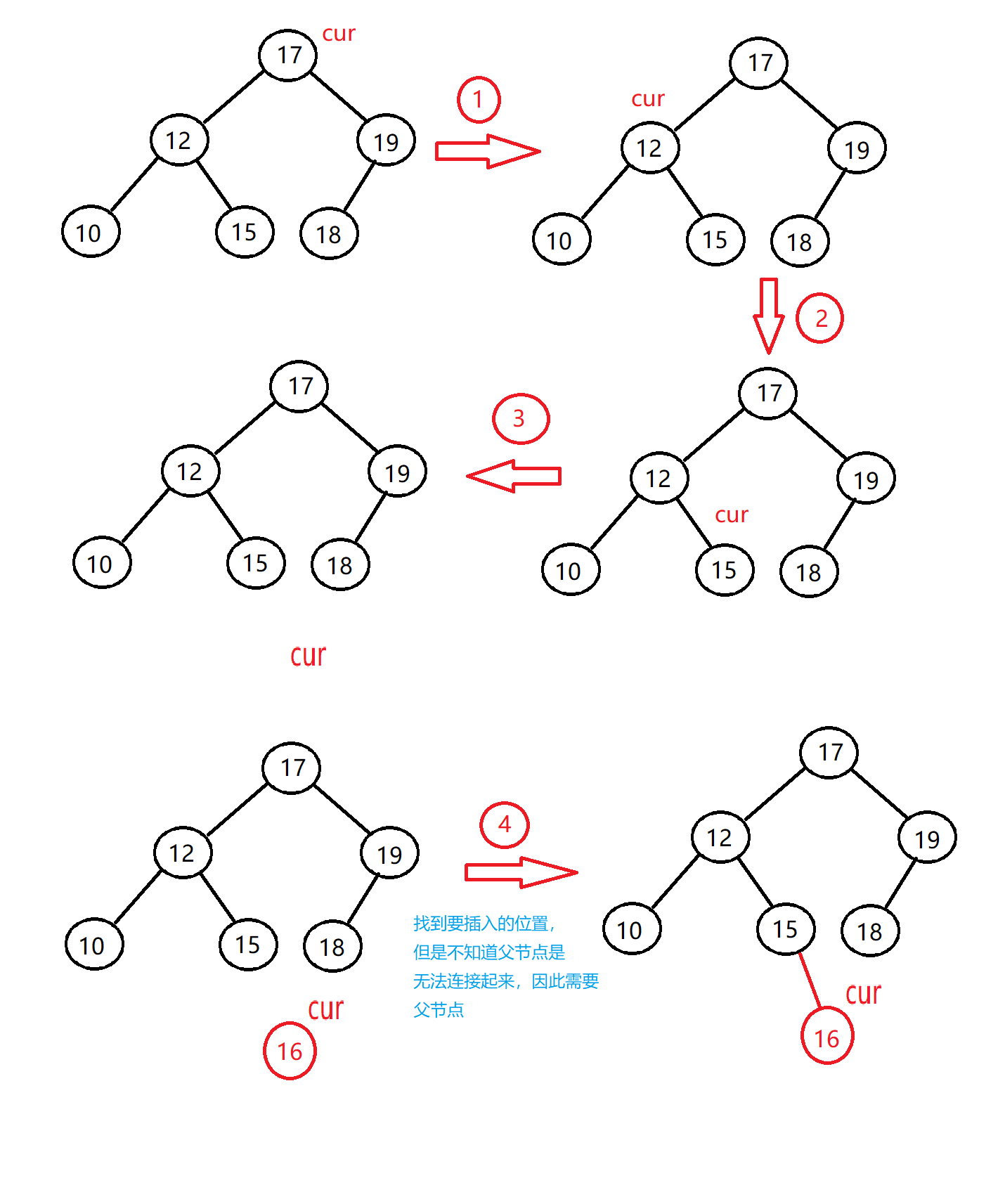
1、删除的节点没有孩子:

  1. 找到该节点以及父节点。
  2. 该节点如果是父节点的左孩子，将父节点的左孩子置空。
  3. 该节点如果是父节点的右孩子，将父节点的右孩子置空。

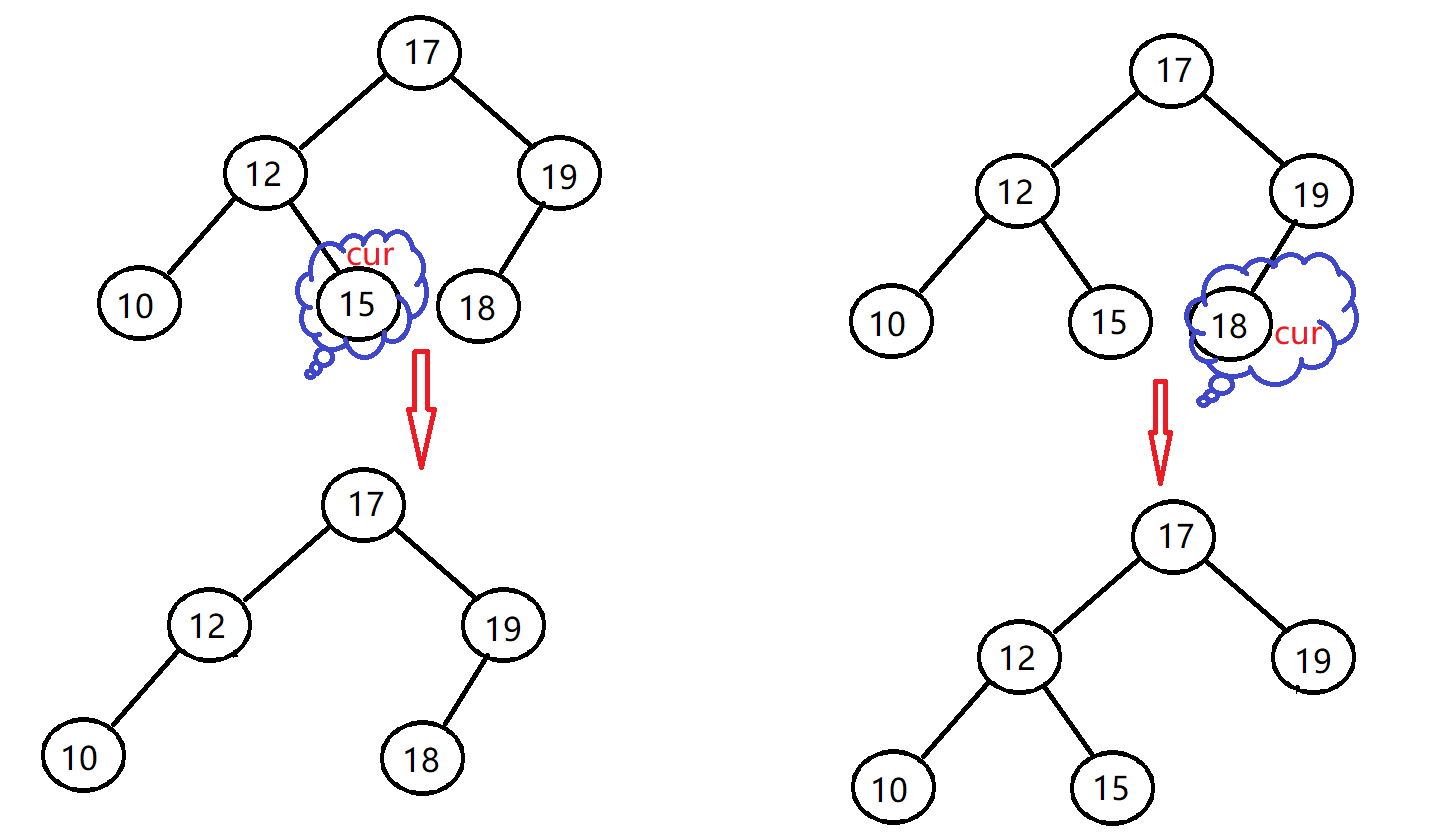
image-20240318132133791

2、删除的节点只有一个孩子

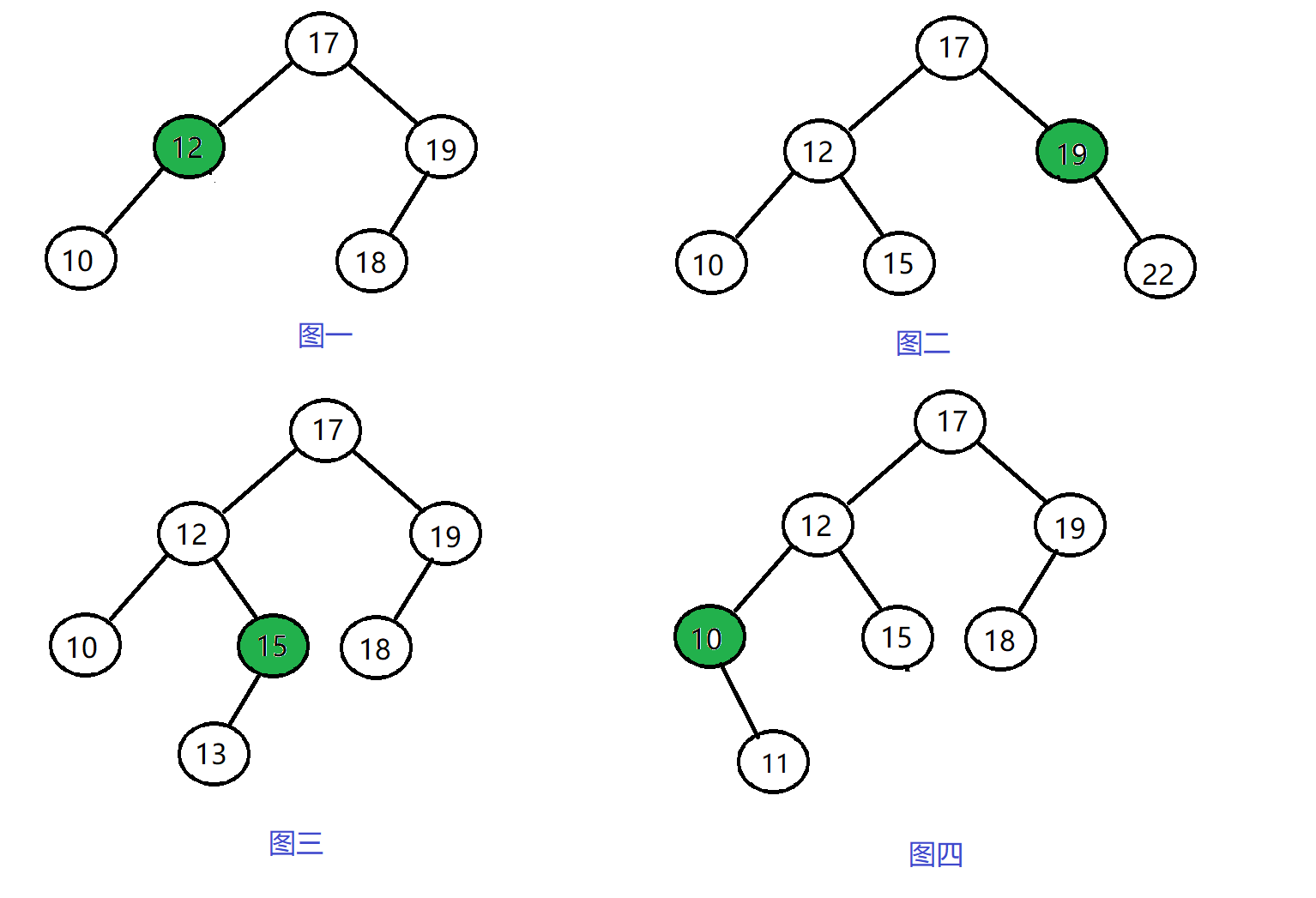
  1. 如果该节点只有左孩子，将该节点的左孩子交给父亲去管。
    • 该节点有可能是某子树的左子树或者右子树，如图一图三。
  2. 如果该节点只有右孩子，将该节点的右孩子交给父亲去管。
    • 该节点有可能是某子树的左子树或者右子树，如图二图四。
  3. 对于图五图六删除的结点恰好是只有一个孩子的根节点，也要分析处理。

image-20240318135647020

image-20240318212915976

代码实现：

bool Erase(const K& key)
{
    Node* parent = nullptr;
    Node* cur = _root;
    while(cur)
    {
        // 1、找到要删除的节点
        if(cur->_key < key)
        {
            parent = cur;
            cur = cur->_right;
        }
        else if(cur->_key > key)
        {
            parent = cur;
            cur = cur->_left;
        }
        else
        {
            // 找到该节点
            // 1、该节点的左子树为空
            if(cur->_left == nullptr)
            {
                if(cur == _root)
                {
                    _root = cur->_right;
				}
                else
                {
                    // 1、该节点是父亲的右孩子
                    if(cur == parent->_right)
                    {
                        parent->_right = cur->_right;
                    }
                    // 2、该节点是父亲的左孩子
                    else
                    {
                        parent->_left = cur->_right;
                    }
                }
                
                delete cur;
                return true;
            }
            // 2、该节点的右子树为空
            else if(cur->_right == nullptr)
            {
                if(cur == _root)
                {
                    _root = cur->_left;
                }
                else
                {
                    // 1、该节点是父亲的左孩子
                    if(cur == parent->_left)
                    {
                        parent->_left = cur->_left;
                    }
                    // 2、该节点是父亲的右孩子
                    else
                    {
                        parent->_right = cur->_left;
                    }
                }
                delete cur;
            	return true;
            }
        }
    }
    return false;
}

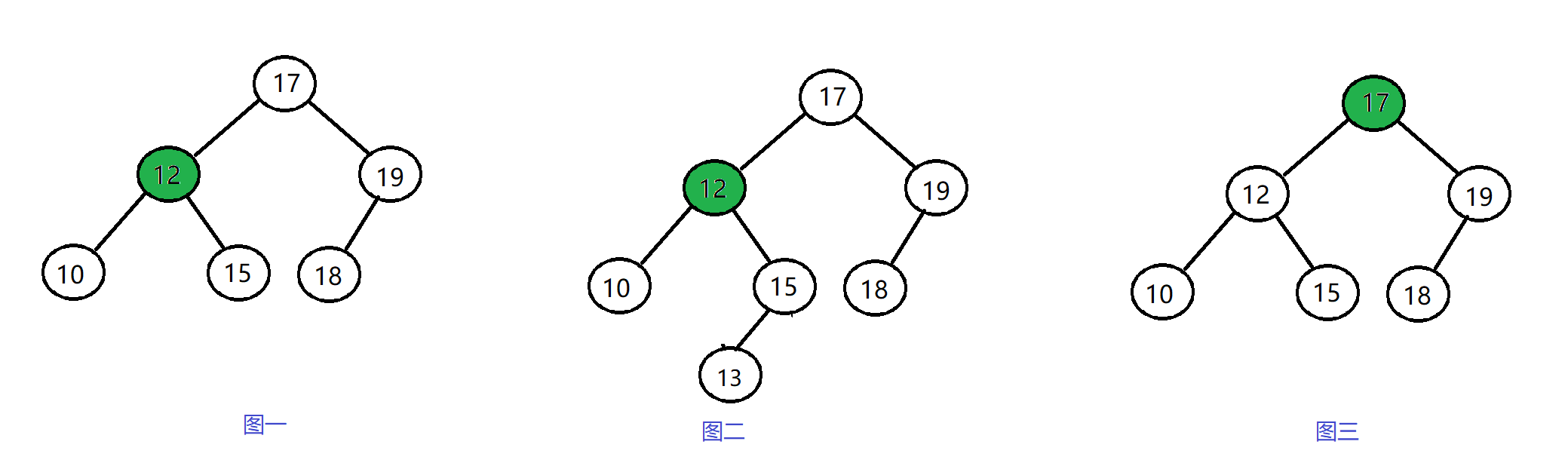
3、删除的节点有两个孩子

  1. 找到该节点及父亲节点。
  2. 将该节点的右子树中的最小结点的值或者左子树中的最大结点的值赋值给该节点。
  3. 将左子树的最大结点或者右子树的最小结点的父亲结点进行处理分析。(该结点有可能没孩子，有可能有一个孩子)

image-20240318144120720

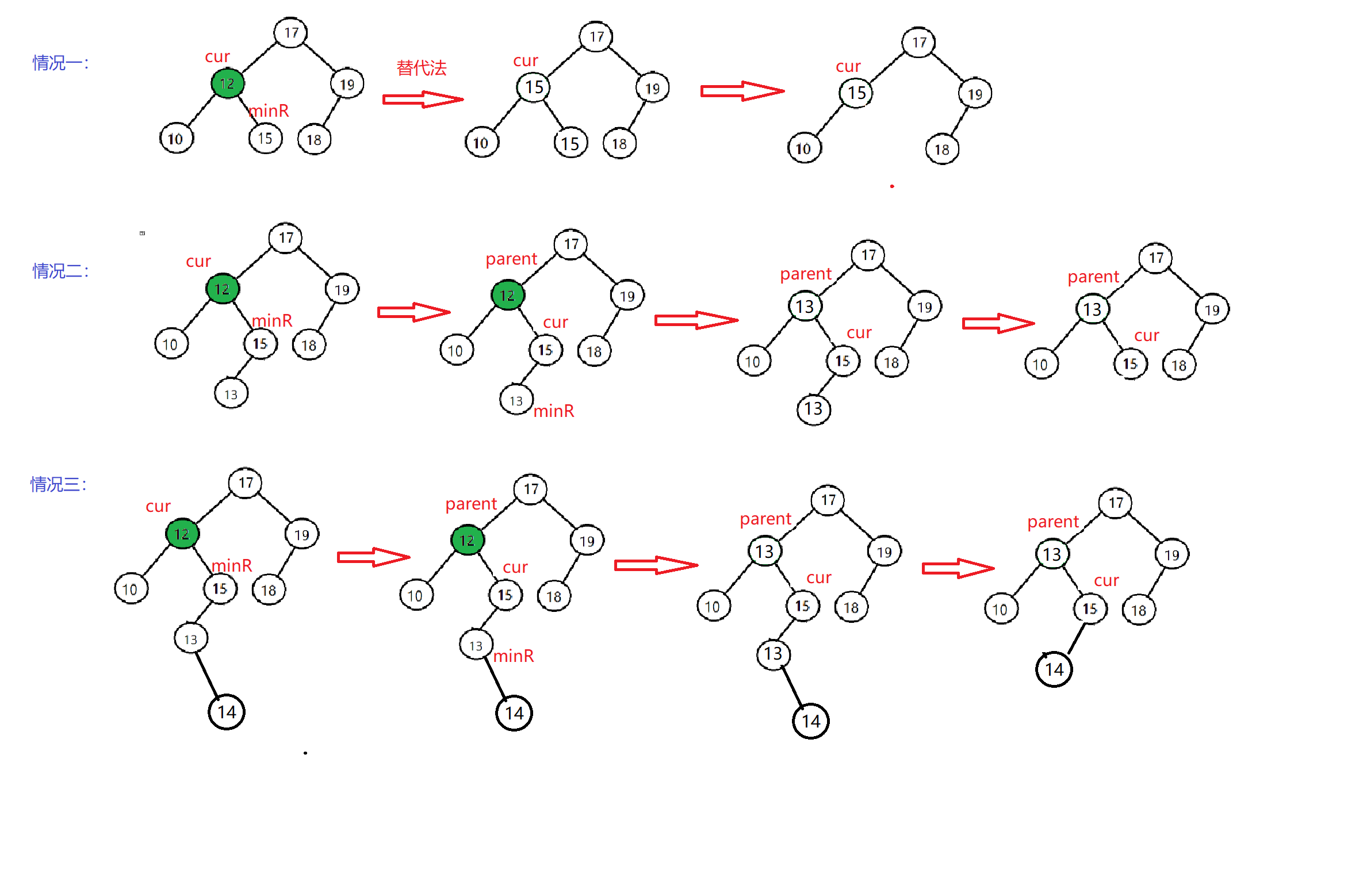
image-20240318154820960

代码实现

  1. 这样写是否正确？

    Node* parent = nullptr;
Node* minR = cur->_right;
while(minR->_left)
{
	parent = cur;
	minR = minR->_left;
}
cur->_key = minR->_key;

if(parent->_right == minR)
{
	parent->_left = nullptr;
}
else
{
	parent->_right = nullptr;
}
delete minR;

上述代码有几个问题：

  1. 第一行将parent置为空，对于情况一来说，不会进入循环中，并且第十行要对空指针解引用。
  2. 第十二行将nullptr赋值给自己的父亲节点的左孩子或者右孩子，但是有可能是情况三。此时就转变成了局部子树中删除只有一个孩子的结点，不可能有两个孩子，一旦有两个孩子，还会继续先下寻找左子树的。

正确的代码实现：

Node* minR_parent = cur;
Node* minR = cur->_right;
while(minR->_left)
{
	minR_parent = minR;
	minR = minR->_left;
}
cur->_key = minR->_key;

if(minR_parent->_right == minR)
{
	minR_parent->_left = minR->_right;
}
else
{
	minR_parent->_right = minR->_right;
}
delete minR;

删除12，调试时进入到这个函数内部：

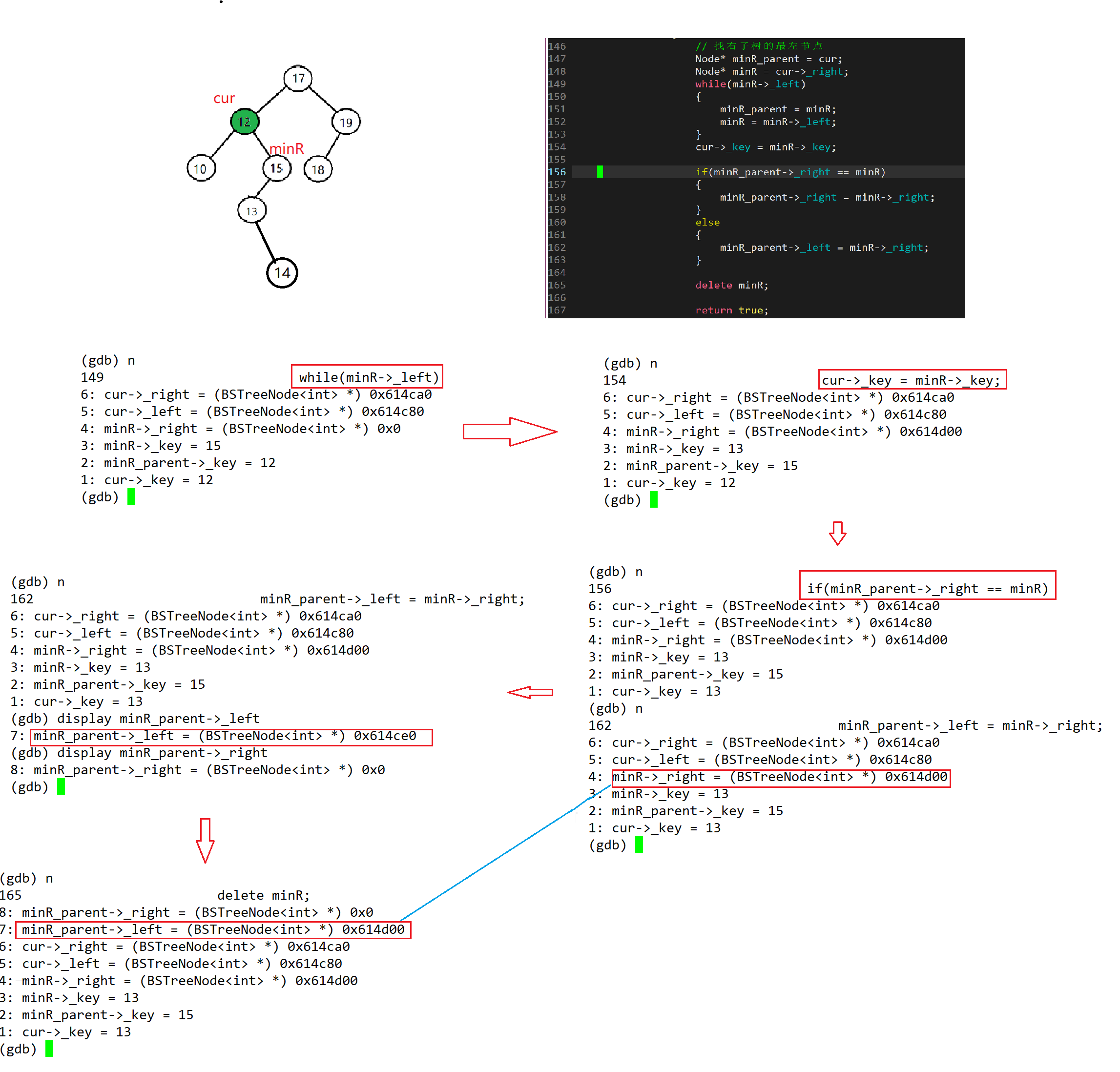
image-20240318180336863

执行165行delete时，其实没什么变化。因为minR是内置类型，编译器不处理。除非自己写析构~~

  • 主函数：数据是情况三的数据

    #include "BSTree.hpp"

int main()
{
    int arr[] = {17, 12, 19, 10 ,15, 18, 13, 14};
    BSTree<int> t1;

    for(auto& ch : arr)
    {
        t1.Insert(ch);
    }

    t1.MidOrder();
    return 0;
}

image-20240318175931129

效率

对于有序的数据而言，很容易形成单支，因此时间复杂度为O(N)。通过控制平衡，从而有了平衡二叉树(AVL),时间复杂度为严格的O(logN)。

一般情况而言，时间复杂度为O(logN)。

avatar
文章
阅读
粉丝