2368. 受限条件下可到达节点的数目
BFS ⟮O(n)⟯
class Solution:
def reachableNodes(self, n: int, edges: List[List[int]], restricted: List[int]) -> int:
r = set(restricted)
g = [[] for _ in range(n)]
for u, v in edges:
if u not in r and v not in r:
g[u].append(v)
g[v].append(u)
res = 0
q = deque([0])
visited = set()
while q:
node = q.popleft()
visited.add(node)
res += 1
for nxt in g[node]:
if nxt not in visited:
q.append(nxt)
return res
class Solution {
public:
int reachableNodes(int n, vector<vector<int>>& edges, vector<int>& restricted) {
unordered_set<int> r(restricted.begin(), restricted.end());
vector<vector<int>> g(n);
for (auto e : edges){
int u = e[0], v = e[1];
if (!r.contains(u) && !r.contains(v)){
g[u].emplace_back(v);
g[v].emplace_back(u);
}
}
queue<int> q{{0}};
int res = 0;
unordered_set<int> visited;
visited.emplace(0);
while (!q.empty()){
int node = q.front(); q.pop();
res += 1;
for (int nxt : g[node]){
if (!visited.contains(nxt)){
visited.emplace(nxt);
q.push(nxt);
}
}
}
return res;
}
};
DFS ⟮O(n)⟯
class Solution:
def reachableNodes(self, n: int, edges: List[List[int]], restricted: List[int]) -> int:
r = set(restricted)
g = [[] for _ in range(n)]
for u, v in edges:
if u not in r and v not in r:
g[u].append(v)
g[v].append(u)
def dfs(u, pa):
cnt = 1
for v in g[u]:
if v != pa:
cnt += dfs(v, u)
return cnt
return dfs(0, -1)
class Solution {
vector<vector<int>> g;
int dfs(int u, int pa){
int cnt = 1;
for (int v : g[u]){
if (v != pa){
cnt += dfs(v, u);
}
}
return cnt;
};
public:
int reachableNodes(int n, vector<vector<int>>& edges, vector<int>& restricted) {
unordered_set<int> r(restricted.begin(), restricted.end());
g.resize(n);
for (auto e : edges){
int u = e[0], v = e[1];
if (!r.contains(u) && !r.contains(v)){
g[u].emplace_back(v);
g[v].emplace_back(u);
}
}
return dfs(0, -1);
}
};

class Solution {
public:
int reachableNodes(int n, vector<vector<int>>& edges, vector<int>& restricted) {
unordered_set<int> r(restricted.begin(), restricted.end());
vector<vector<int>> g(n);
for (auto e : edges){
int u = e[0], v = e[1];
if (!r.contains(u) && !r.contains(v)){
g[u].emplace_back(v);
g[v].emplace_back(u);
}
}
function<int(int, int)> dfs = [&] (int u, int pa){
int cnt = 1;
for (int v : g[u]){
if (v != pa){
cnt += dfs(v, u);
}
}
return cnt;
};
return dfs(0, -1);
}
};

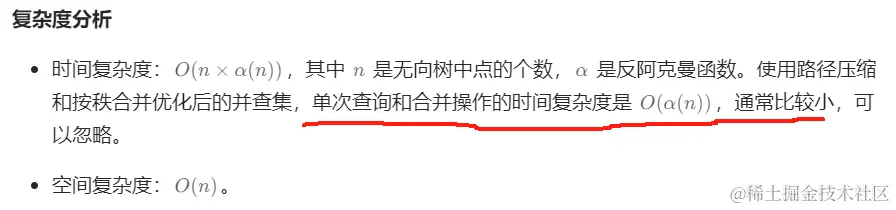
并查集 ⟮O(n×α(n))、O(n)⟯

class UnionFind:
def __init__(self, n):
self.parent = list(range(n))
self.rank = [0] * n
def find(self, x):
if self.parent[x] != x:
self.parent[x] = self.find(self.parent[x])
return self.parent[x]
def union(self, x, y):
rootx = self.find(x)
rooty = self.find(y)
if rootx != rooty:
if self.rank[rootx] < self.rank[rooty]:
self.parent[rootx] = rooty
elif self.rank[rootx] > self.rank[rooty]:
self.parent[rooty] = rootx
else:
self.parent[rooty] = rootx
self.rank[rootx] += 1
def count(self):
cnt = 0
root0 = self.find(0)
for i in range(len(self.parent)):
if root0 == self.find(i):
cnt += 1
return cnt
class Solution:
def reachableNodes(self, n: int, edges: List[List[int]], restricted: List[int]) -> int:
r = set(restricted)
uf = UnionFind(n)
for u, v in edges:
if u not in r and v not in r:
uf.union(u, v)
return uf.count()
class UnionFind{
public:
UnionFind(int n) : parent(n), rank(n){
for (int i = 1; i < n; ++i){
parent[i] = i;
}
}
int find(int x){
if (parent[x] != x){
x = find(parent[x]);
}
return parent[x];
}
void merge(int x, int y){
int rootx = find(x);
int rooty = find(y);
if (rootx != rooty){
if (rank[rootx] > rank[rooty]){
parent[rooty] = rootx;
}else if (rank[rootx] < rank[rooty]){
parent[rootx] = rooty;
}else{
parent[rooty] = rootx;
++rank[rootx];
}
}
}
int count(){
int cnt = 0;
int root0 = find(0);
for (int i = 0; i < parent.size(); ++i){
if (root0 == find(i)){
cnt++;
}
}
return cnt;
}
private:
vector<int> parent;
vector<int> rank;
};
class Solution {
public:
int reachableNodes(int n, vector<vector<int>>& edges, vector<int>& restricted) {
unordered_set<int> r(restricted.begin(),restricted.end());
UnionFind uf = UnionFind(n);
for (auto e : edges){
if (!r.contains(e[0]) && !r.contains(e[1])){
uf.merge(e[0], e[1]);
}
}
return uf.count();
}
};