《人工智能》第二章 盲目搜索
状态空间图
状态空间图(state-space graph)是对问题的一种表示方法。
下图给出了一棵状态空间树(state-space tree)。状态空间树由节点和分支组成。每个椭圆是一个节点,代表问题的一个状态。节点之间的弧表示将状态空间树移动到新节点的运算符(或应用该运算符的结果)。
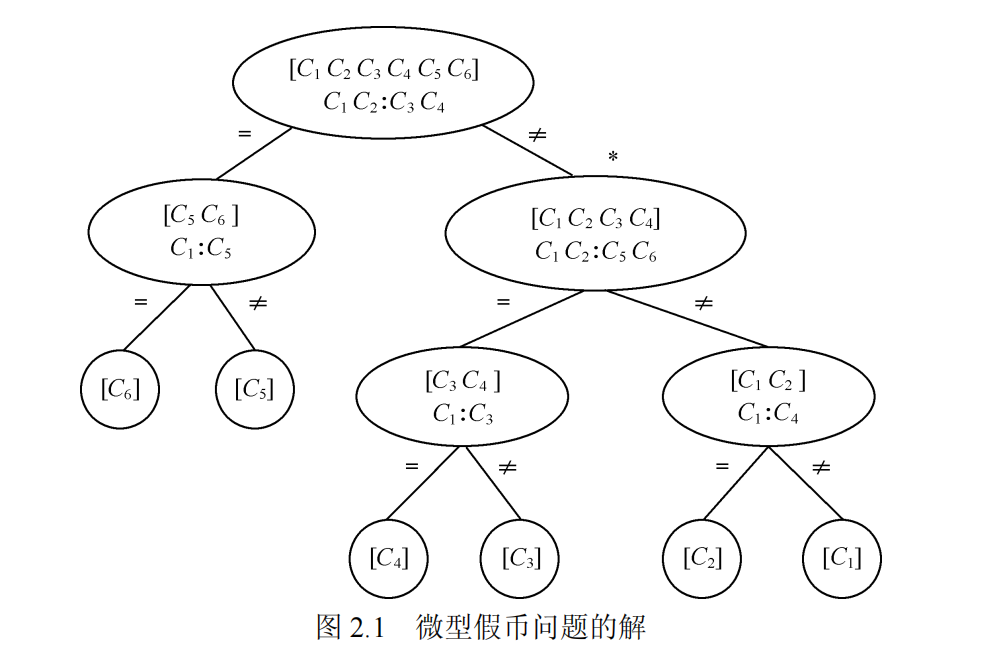
假币问题
有 12 枚硬币,已知其中一枚是假的或伪造的,但是不知道这枚假币比真币轻还是重。为了解决这个问题,通过天平你可以建立一个过程,只需要称三次(每次对两组硬币进行比较),就可以找出那枚假币。
微型假币问题:与假币问题相同,但只涉及6枚硬币。
图2.1中的[C1 C2 C3 C4 C5 C6] 表示假币可能是六枚硬币中的一个,C1 C2和C3 C4相比较之后,如果他们质量不相同,说明假币在C1C2C3C4中,表示为[C1 C2 C3 C4],而如果他们质量相同,说明假币在C5 和 C6中,表示为[C5 C6]
-
问题的状态空间树包含了问题可能出现的所有状态以及这些状态之间所有可能的转换。
-
问题的解通常需要在这个结构中进行搜索(无论它是树还是图),搜索始于起始节点,止于终点或目标状态(goal state)。
-
通常情况下,状态空间图可以包含代表相同问题状态的多个节点。
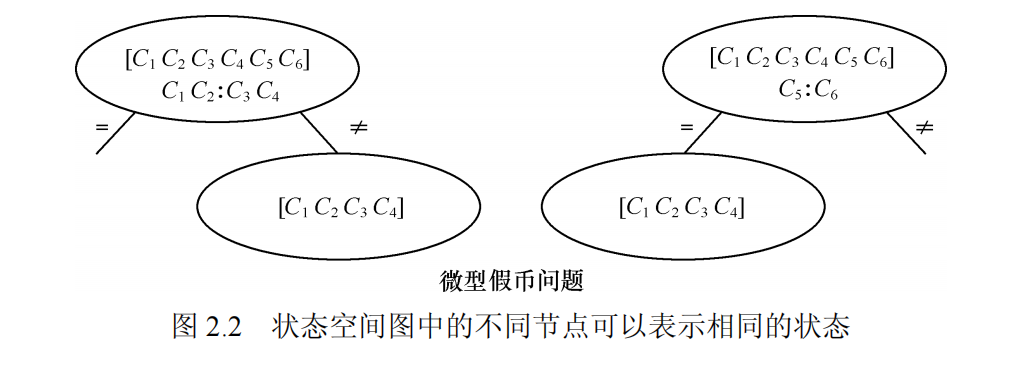
生成——测试范式
问题求解的一种直接方式就是先给出可能的解,再检查每个可能的解,看是否有候选解能
够构成问题的解。这种方式被称为生成-测试范式(generate-and-test paradigm)。
n皇后问题
指的是将 n 个皇后放置在一个 n×n 的棋盘上,使得任何两个皇后都不互相攻击。也就是说,任何两个皇后都不占据相同的行、列或对角线。这些条件被称为问题的约束条件。
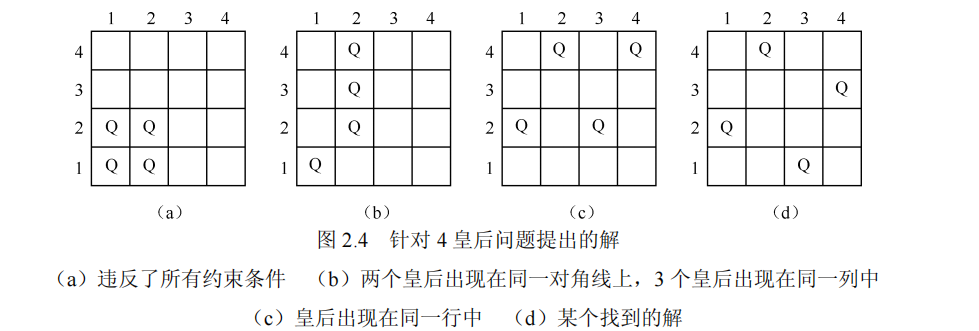
要想找到解,需要探索1820种情况
一个可靠的生成器:
- 完备的,必须提出所有的解
- 知情的,能够排除不可能的情况
- 非冗余的,如果过一个解被拒绝或是成功,则不应该再提出这种情况
生成与测试范式伪代码

回溯法
回溯法也称为试探法,首先暂时放弃关于问题规模大小的限制,并将问题的候选解按某种顺序逐一枚举和检验。
下面考虑将皇后按照一定的顺序摆放在棋格中的过程。假设在第 i 步,前面的第 1, 2, …, i−1 步都成功摆放了皇后,接下来将第 i 个皇后摆放在棋格中。如果第 i 个皇后摆放在任意棋格中都违反约束条件,那么必须返回到第 i—1 步。也就是说,必须回溯考虑摆放第(i—1)个皇后的那一步,以此类推........
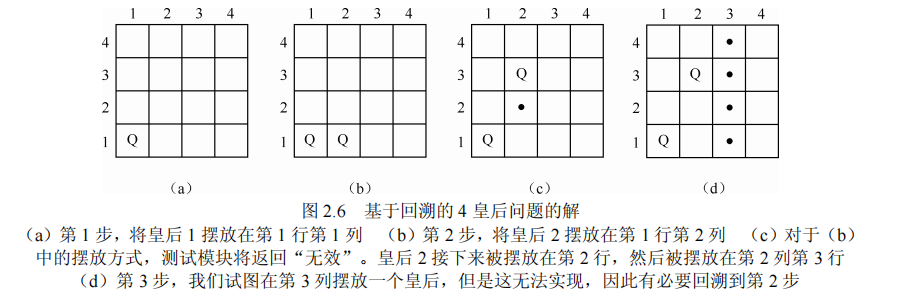
棋盘上皇后的位置可以使用四个行分量的向量来表示,比如:(1,3,-,-)表示图2.6(c)
该向量表示皇后 1 在第 1 列第 1 行,皇后 2 在第 2 列第 3 行,第 3、第 4 个分量则表示皇后3 和皇后 4 还未被放置在剩余的两行中。
接下来回溯到皇后2,把它放到第四行,如下图
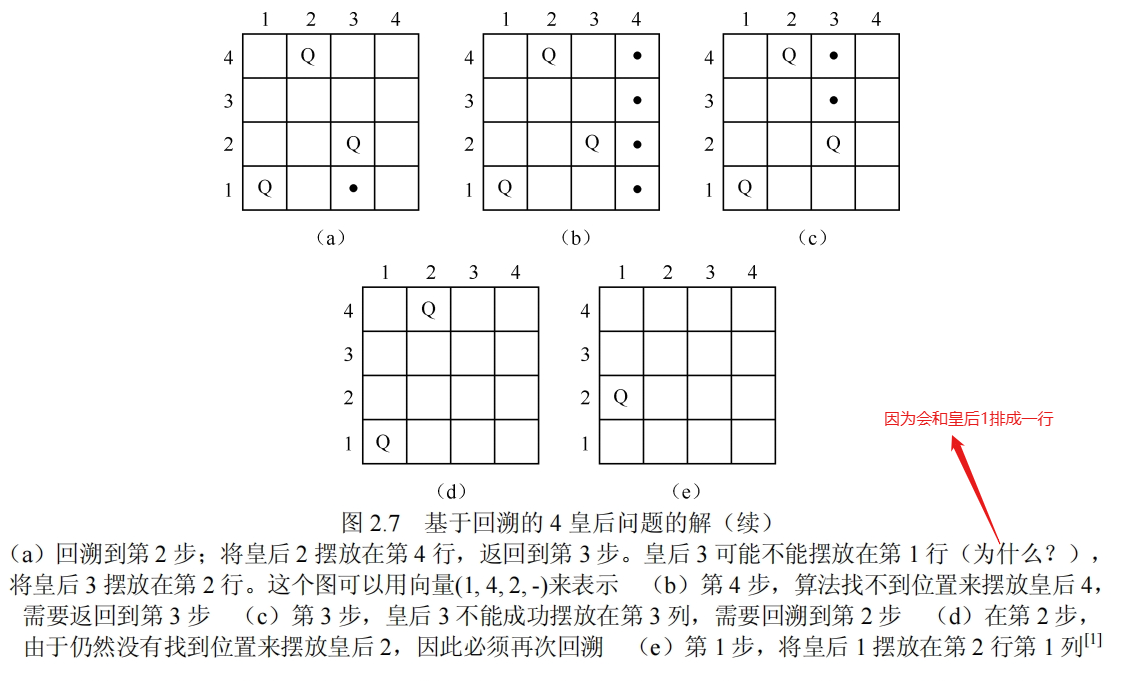
最终回溯到第一步,所以接下来将皇后1放到第二行,并再次试探直到得出第一个解,如下图
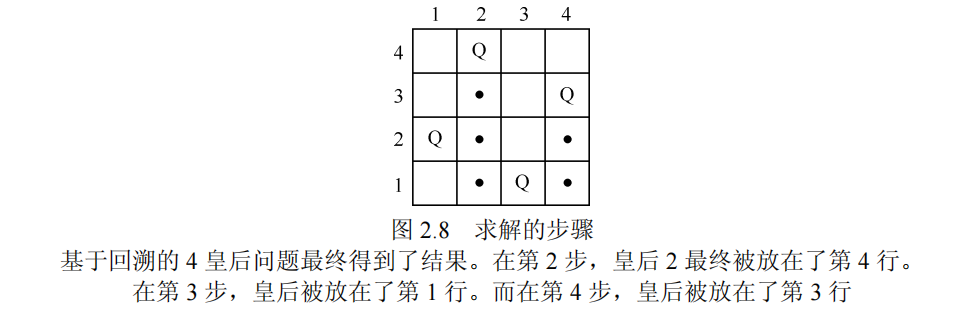
接下来要找出第二个解
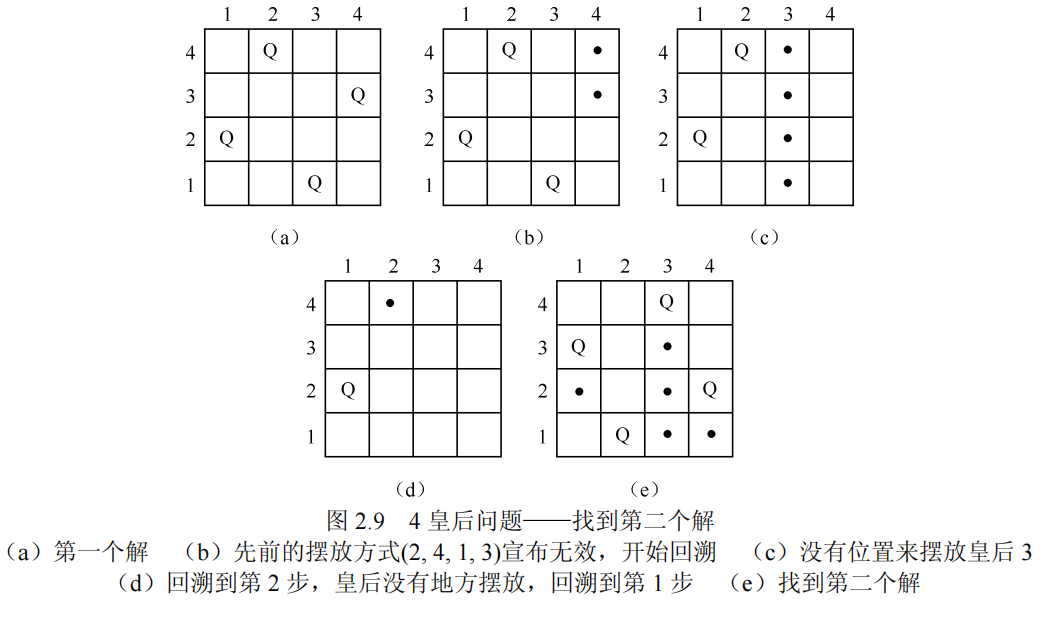
所以找到的两个解为(2,4,1,3),(3,1,4,2)
以上搜索方式还可以用搜索树来表示:
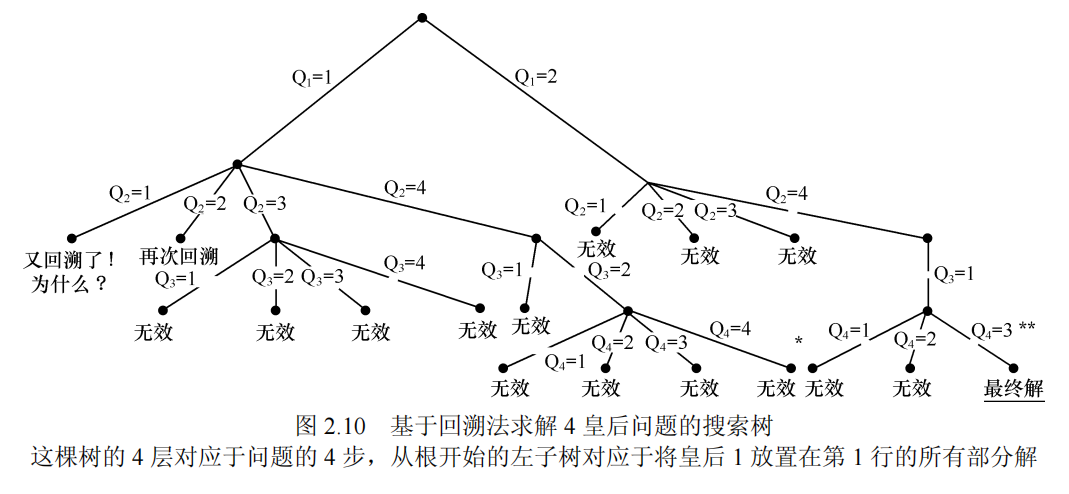
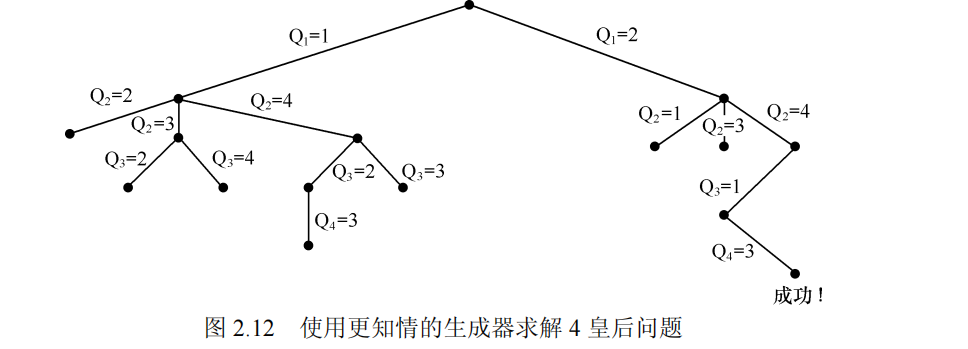
以上两个生成器的区别在于:
前者有4的4次方种可能的情况,而后者全部的可能性最多只有4 ! = 24种。
贪心算法
- 贪心算法是指在对问题求解时,总是做出在当前看来是最好的选择。也就是说,不从整体最优上加以考虑,只做出在某种意义上的局部最优解。
- 贪心算法总是包含一个必须优化(即最大化或最小化)的目标函数(objective function)。