计算机体系结构习题总结第三章 3-6

2024-01-20 17 阅读1分钟

本题出自清华大学出版社计算机系统结构教程第 3 版习题 3-6 。

当流水线各段的时间不完全相等时，流水线的最大吞吐率和实际吞吐率由时间最长的那个段决定，这个段就成为了整个流水线的瓶颈。消除流水线瓶颈的两种方法：

细分瓶颈段；
重复设置瓶颈段。

第一问

\text{TP}=\frac{n}{\displaystyle\sum_{i=1}^k\Delta t_i+(n-1)\max\limits_{1\leq i\leq n}\{\Delta t_i\}}=\frac{10}{(50+50+100+200)+9\times 200}=\frac{1}{220}\text{ns}^{-1}

计算流水线效率的一般公式为

\text{E}=\frac{\text{n}个任务实际占用的时空区面积}{\text{k}个段总的时空区面积}

对于此题

\text{E}=\frac{n\cdot \displaystyle\sum_{i=1}^k\Delta t_i}{k\left[\displaystyle\sum_{i=1}^k\Delta t_i+(n-1)\max\limits_{1\leq i\leq n}\{\Delta t_i\}\right]}=\frac{10\times(50+50+100+200)}{4\times[(50+50+100+200)+9\times 200]}=\frac{5}{11}

第二问

该流水线的瓶颈为第 3 、 4 段。

措施一：细分瓶颈段，将流水线变为八级流水线

此时
$\text{TP}=\frac{n}{\displaystyle\sum_{i=1}^k\Delta t_i+(n-1)\max\limits_{1\leq i\leq n}\{\Delta t_i\}}=\frac{10}{50\times8+9\times 50}=\frac{1}{85}\text{ns}^{-1}$ $\text{E}=\frac{n}{k+n-1}=\frac{10}{17}$
措施二：重复设置部件

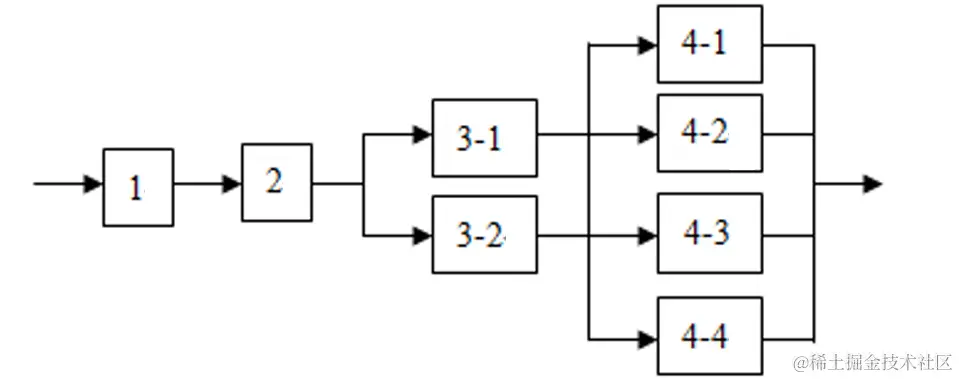
在这种情况下，流水线的时空图为

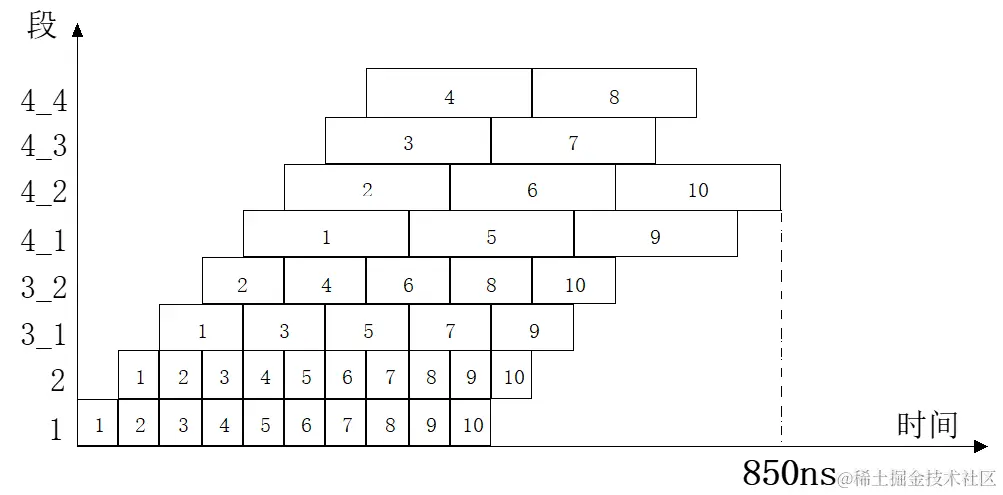
效率为
$\text{E}=\frac{400\times10}{850\times8}=\frac{10}{17}$