二叉树
种类:
- 满二叉树
- 完全二叉树
- 二叉搜索树
- 平衡二叉搜索树(map、set等)
存储方式:
-
线性存储
若数组下标从 0 开始,则下标为 i 的元素的
左孩子下标:
2*i+1右孩子下标:
2*i+2 -
链式存储
遍历方式:
- 深度优先搜索(递归法、迭代法)
- 前序遍历(根左右)
- 中序遍历(左根右)
- 后序遍历(左右根)
- 广度优先搜索(迭代法)
- 层序遍历
定义方式:
function TreeNode(val, left, right) {
this.val = (val===undefined ? 0 : val)
this.left = (left===undefined ? null : left)
this.right = (right===undefined ? null : right)
}
深度与高度:
-
节点的深度:指从根节点到该节点的最长简单路径边的条数或者节点数(取决于深度从0开始还是从1开始)——使用前序求的是深度
-
节点的高度:指从该节点到叶子节点的最长简单路径边的条数后者节点数(取决于高度从0开始还是从1开始)——使用后序求的是高度
(一般都是使用后序)
递归三部曲
- 确定递归函数的参数和返回值
- 确定终止条件
- 确定单层递归的逻辑
1. 二叉树的遍历
二叉树的前序遍历
思路:
-
递归法
- 确定函数的参数为当前遍历节点和用来存放遍历结果的数组,函数的返回值为用来存放遍历结果的数组
- 确定函数的终止条件为当前遍历节点为空
- 确定单层递归的逻辑:
- 先将当前遍历节点的值放入结果数组中 (根)
- 然后递归遍历左子树 (左)
- 再递归遍历右子树 (右)
-
迭代法
用栈结构存储待扩展节点
- 如果根节点为空,则直接返回
[](空数组) - 将
root节点放入栈中 - 利用循环遍历树,终止条件为:栈空
- 循环体:
- 先取出栈顶元素,将其值放入结果数组中;
- 然后,若其右孩子节点非空,则将右孩子节点放入栈中;
- 再,若其左孩子节点非空,则将左孩子节点放入栈中(由于栈是先进后出,所以前序遍历待扩展集合中需要先放入右再放入左)
- 最后,返回结果数组
动画效果:
- 如果根节点为空,则直接返回
代码:
-
递归法
/** * Definition for a binary tree node. * function TreeNode(val, left, right) { * this.val = (val===undefined ? 0 : val) * this.left = (left===undefined ? null : left) * this.right = (right===undefined ? null : right) * } */ /** * @param {TreeNode} root * @return {number[]} */ var preorderTraversal = function (root, res = []) { if (!root) return res res.push(root.val) preorderTraversal(root.left, res) preorderTraversal(root.right, res) return res }; -
迭代法
/** * Definition for a binary tree node. * function TreeNode(val, left, right) { * this.val = (val===undefined ? 0 : val) * this.left = (left===undefined ? null : left) * this.right = (right===undefined ? null : right) * } */ /** * @param {TreeNode} root * @return {number[]} */ var preorderTraversal = function (root) { let res = [] if (!root) return res let stack = [root] while (stack.length) { let tmp = stack.pop() res.push(tmp.val) tmp.right && stack.push(tmp.right) tmp.left && stack.push(tmp.left) } return res };
二叉树的中序遍历
思路:
-
递归法
- 确定递归函数的参数和返回值:同前序遍历
- 确定函数的终止条件:同前序遍历
- 确定单层递归的逻辑(和前序遍历的基本思路一样,只需改变访问顺序即可):
- 先递归遍历左子树 (左)
- 再将当前遍历节点的值放入结果数组中 (根)
- 然后递归遍历右子树 (右)
-
迭代法
由于处理顺序和访问顺序是不一致的,所以就需要借用指针的遍历来帮助访问节点,栈则用来处理节点上的元素
-
利用
current指针指向当前遍历节点,初始其指向树的根节点 -
利用循环遍历树,终止条件为:当前遍历节点为空且栈空
-
循环体:
- 如果当前遍历节点非空,则将其加入栈中,并且
current指针移向其左孩子节点(一直遍历左孩子) - 如果当前遍历节点为空,则弹出栈顶元素并将其值放入结果数组中,
current指针移向其右孩子节点
- 如果当前遍历节点非空,则将其加入栈中,并且
-
最后,返回结果数组
动画效果:
-
代码:
-
递归法
/** * Definition for a binary tree node. * function TreeNode(val, left, right) { * this.val = (val===undefined ? 0 : val) * this.left = (left===undefined ? null : left) * this.right = (right===undefined ? null : right) * } */ /** * @param {TreeNode} root * @return {number[]} */ var inorderTraversal = function (root, res = []) { if (!root) return res inorderTraversal(root.left, res) res.push(root.val) inorderTraversal(root.right, res) return res }; -
迭代法
/** * Definition for a binary tree node. * function TreeNode(val, left, right) { * this.val = (val===undefined ? 0 : val) * this.left = (left===undefined ? null : left) * this.right = (right===undefined ? null : right) * } */ /** * @param {TreeNode} root * @return {number[]} */ var inorderTraversal = function (root) { let res = [] let stack = [] let current = root while (current || stack.length) { if (current) { stack.push(current) current = current.left } else { current = stack.pop() res.push(current.val) current = current.right } } return res };
二叉树的后序遍历
思路:
-
递归法
- 确定递归函数的参数和返回值:同前序遍历、中序遍历
- 确定函数的终止条件:同前序遍历、中序遍历
- 确定单层递归的逻辑(和前序遍历、中序遍历的基本思路一样,只需改变访问顺序即可):
- 先递归遍历左子树 (左)
- 再递归遍历右子树 (右)
- 然后将当前遍历节点的值放入结果数组中 (根)
-
迭代法
和前序遍历的基本思路一样,只需改变部分顺序即可
根左右 --> 根右左 --> 左右根
故,在前序遍历代码的基础上,改变左右节点加入栈的顺序,并将最终的结果数组逆序返回即可
代码:
-
递归法
/** * Definition for a binary tree node. * function TreeNode(val, left, right) { * this.val = (val===undefined ? 0 : val) * this.left = (left===undefined ? null : left) * this.right = (right===undefined ? null : right) * } */ /** * @param {TreeNode} root * @return {number[]} */ var postorderTraversal = function (root, res = []) { if (!root) return res postorderTraversal(root.left, res) postorderTraversal(root.right, res) res.push(root.val) return res }; -
迭代法
/** * Definition for a binary tree node. * function TreeNode(val, left, right) { * this.val = (val===undefined ? 0 : val) * this.left = (left===undefined ? null : left) * this.right = (right===undefined ? null : right) * } */ /** * @param {TreeNode} root * @return {number[]} */ var postorderTraversal = function (root) { let res = [] if (!root) return res let stack = [root] while (stack.length) { let tmp = stack.pop() res.push(tmp.val) tmp.left && stack.push(tmp.left) tmp.right && stack.push(tmp.right) } for (let i = 0; i < Math.floor(res.length / 2); i++) [res[i], res[res.length - 1 - i]] = [res[res.length - 1 - i], res[i]] return res };
二叉树的层序遍历
思路:
用队列存储待扩展节点
-
如果根节点为空,则直接返回
[](空数组) -
将根节点放入队列中
-
利用循环遍历树,终止条件为队空
-
循环体:
-
将当前队列长度保存
-
利用循环,将每层遍历结果放入一个临时数组中保存(保存的队列长度即为当前遍历层节点的个数)
-
循环体:
- 队首元素出队并将其值存入结果数组中
- 若队首元素左子树非空,则将其左子树节点放入队列中
- 若队首元素右子树非空,则将其右子树节点也放入队列中
-
将临时数组中的数据整体放入结果数组中
-
-
最后,返回结果数组
动画效果:
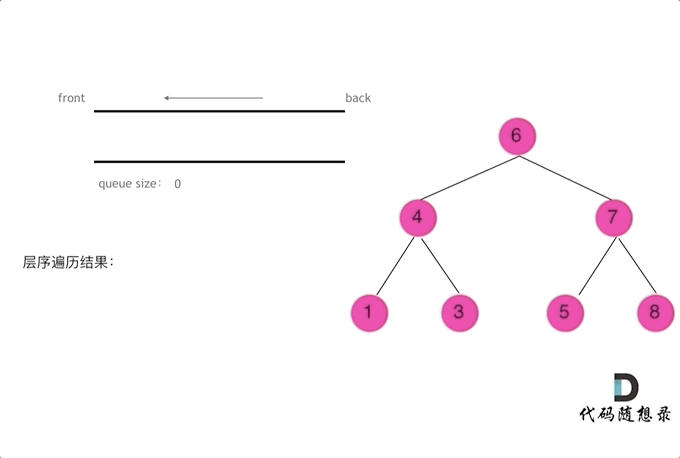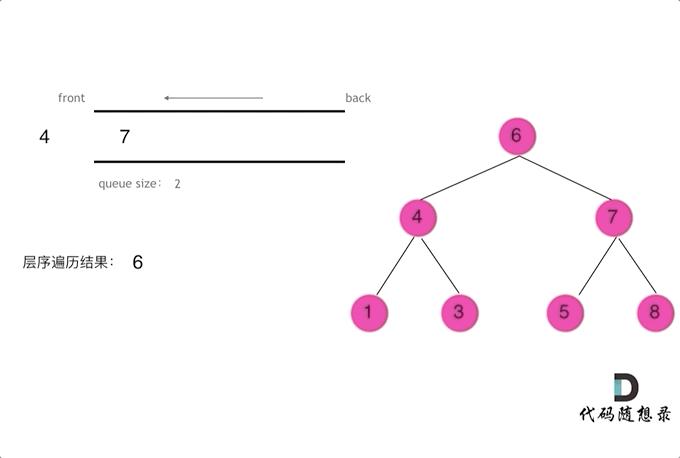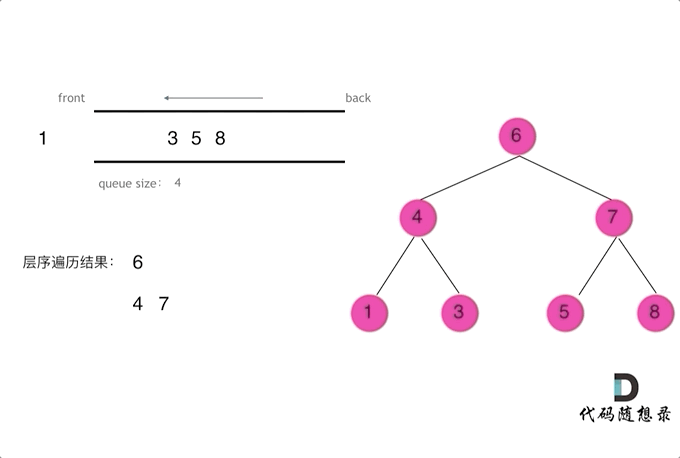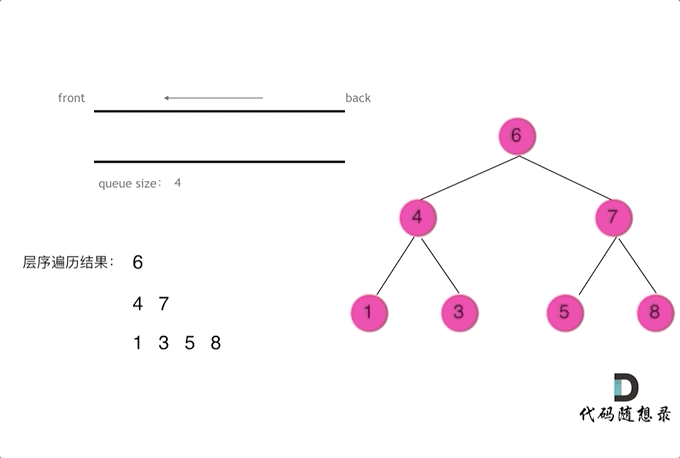
代码:
广度优先搜索
/**
* Definition for a binary tree node.
* function TreeNode(val, left, right) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
*/
/**
* @param {TreeNode} root
* @return {number[][]}
*/
var levelOrder = function (root) {
if (!root) return []
let queue = [root]
let res = []
while (queue.length) {
let len = queue.length
let rest = []
for (let i = 0; i < len; i++) {
let tmp = queue.shift()
rest.push(tmp.val)
tmp.left && queue.push(tmp.left)
tmp.right && queue.push(tmp.right)
}
res.push(rest)
}
return res
};
2. 翻转二叉树
题目:
给你一棵二叉树的根节点 root ,翻转这棵二叉树,并返回其根节点。
思路:
-
利用前中后序遍历(递归法)
- 确定递归函数的参数为当前遍历节点,返回值为翻转后的二叉树的根节点
- 确定终止条件为当前遍历节点为空
- 确定单层递归的逻辑(根据不同遍历调整对应顺序和部分逻辑):
- 将当前遍历节点的左右节点交换
- 递归遍历翻转当前遍历节点的左子树的左右子树
- 递归遍历翻转当前遍历节点的右子树的左右子树
动画效果(前序):
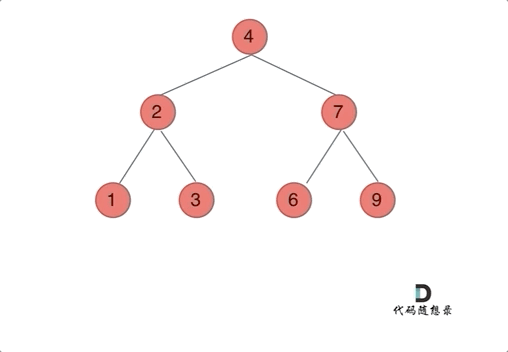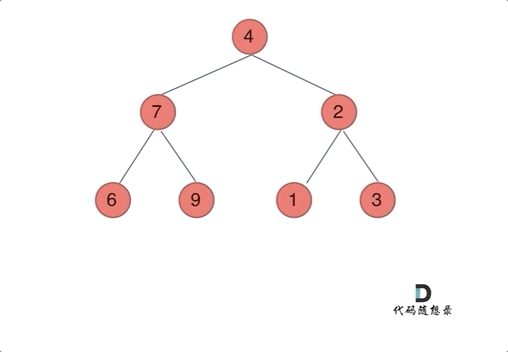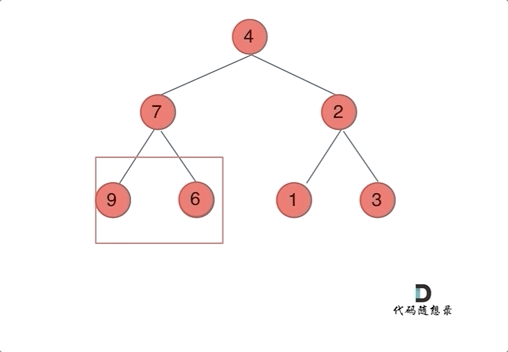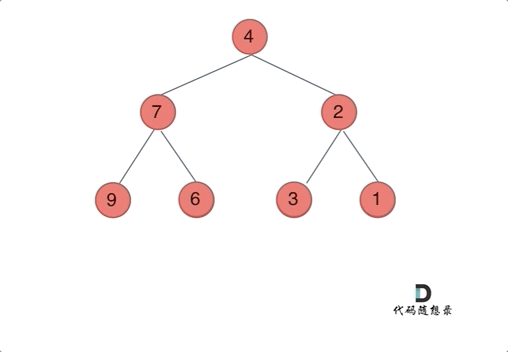
-
利用层序遍历(迭代法)
-
如果根节点为空,则直接返回
[](空数组) -
将根节点放入队列中
-
利用循环遍历翻转二叉树,终止条件为:队空
-
循环体:
- 将队首元素出队
- 交换出队元素的左右子树
- 将出队元素的左右子树节点依次入队(左右节点非空)
-
最后,返回翻转后的二叉树的根节点
-
代码:
-
前序遍历翻转
/** * Definition for a binary tree node. * function TreeNode(val, left, right) { * this.val = (val===undefined ? 0 : val) * this.left = (left===undefined ? null : left) * this.right = (right===undefined ? null : right) * } */ /** * @param {TreeNode} root * @return {TreeNode} */ var invertTree = function (root) { if (!root) return root let tmp = root.left root.left = root.right root.right = tmp invertTree(root.left) invertTree(root.right) return root }; -
后序遍历翻转
/** * Definition for a binary tree node. * function TreeNode(val, left, right) { * this.val = (val===undefined ? 0 : val) * this.left = (left===undefined ? null : left) * this.right = (right===undefined ? null : right) * } */ /** * @param {TreeNode} root * @return {TreeNode} */ var invertTree = function (root) { if (!root) return root invertTree(root.left) invertTree(root.right) let tmp = root.left root.left = root.right root.right = tmp return root }; -
层序遍历翻转
/** * Definition for a binary tree node. * function TreeNode(val, left, right) { * this.val = (val===undefined ? 0 : val) * this.left = (left===undefined ? null : left) * this.right = (right===undefined ? null : right) * } */ /** * @param {TreeNode} root * @return {TreeNode} */ var invertTree = function (root) { if (!root) return root let queue = [root] while (queue.length) { let t = queue.pop() let tmp = t.left t.left = t.right t.right = tmp t.left && queue.push(t.left) t.right && queue.push(t.right) } return root }; -
中序遍历翻转(不推荐)
/** * Definition for a binary tree node. * function TreeNode(val, left, right) { * this.val = (val===undefined ? 0 : val) * this.left = (left===undefined ? null : left) * this.right = (right===undefined ? null : right) * } */ /** * @param {TreeNode} root * @return {TreeNode} */ var invertTree = function (root) { if (!root) return root invertTree(root.left) let tmp = root.left root.left = root.right root.right = tmp invertTree(root.left) return root };
3. 对称二叉树
题目:
给你一个二叉树的根节点 root , 检查它是否轴对称。
思路:
-
递归法
- 确定递归函数的参数为左子树节点、右子树节点,返回值为两个子树的对称情况(
true或false或值为布尔值的表达式) - 确定终止条件为:
-
左右子树节点至少一个为空
或
-
左右子树节点均不空但值不同
-
- 确定单层递归的逻辑:
- 递归对比左节点的左右子节点
- 递归对比右节点的左右子节点
- 确定递归函数的参数为左子树节点、右子树节点,返回值为两个子树的对称情况(
-
非递归法
- 如果根节点为空,则直接返回
true - 将根节点的左右子节点依次放入队列中
- 利用循环对比对应位置节点值是否相同,终止条件为:队空
- 循环体:
- 每次弹出队列的前两个元素,依次为左节点、右节点
- 若这两个元素都空,则开启新一轮循环
- 若这两个元素一个为空一个非空,则直接返回
false - 若这两个元素值不相同,则直接返回
false - 否则,将左节点的左子树节点、右节点的右子树节点、左节点的右子树节点、右节点的左子树节点依次入队
- 最终,返回
true
动画效果:
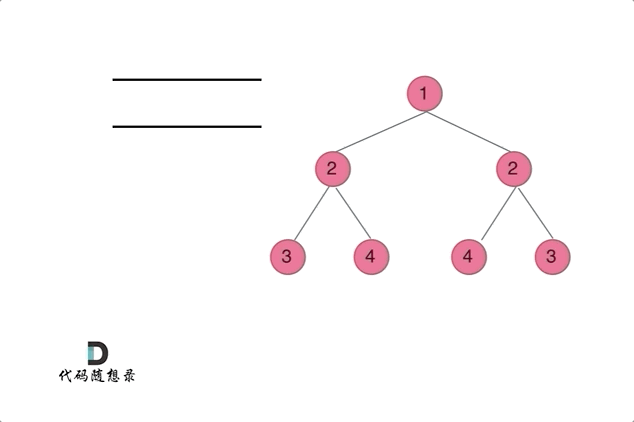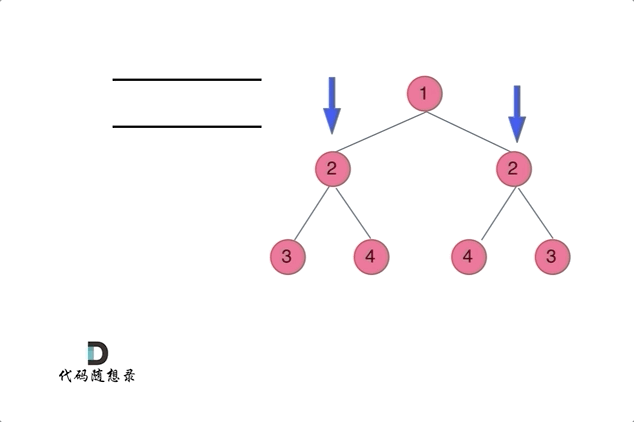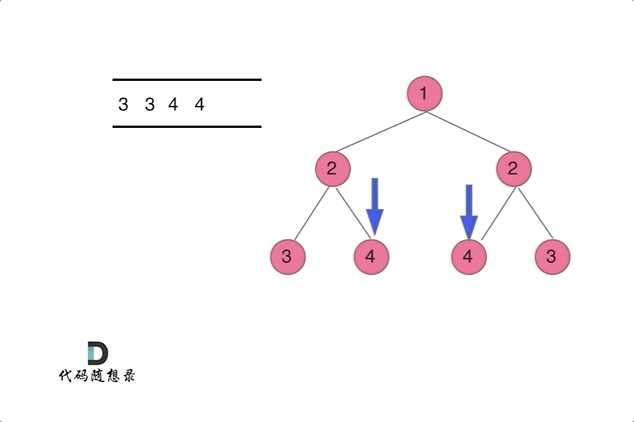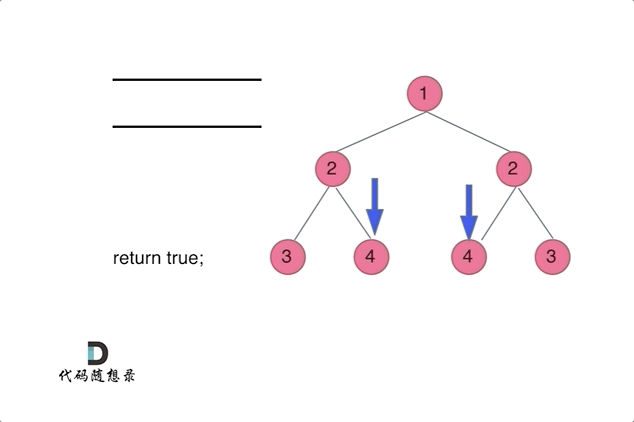
- 如果根节点为空,则直接返回
代码:
-
递归法
/** * Definition for a binary tree node. * function TreeNode(val, left, right) { * this.val = (val===undefined ? 0 : val) * this.left = (left===undefined ? null : left) * this.right = (right===undefined ? null : right) * } */ /** * @param {TreeNode} root * @return {boolean} */ var isSymmetric = function (root) { if (!root) return true return compare(root.left, root.right) }; var compare = function (left, right) { if (left && right && left.val !== right.val) return false else if (!left && !right) return true else if (!left || !right) return false return compare(left.left, right.right) && compare(left.right, right.left) } -
非递归法(队列)
/** * Definition for a binary tree node. * function TreeNode(val, left, right) { * this.val = (val===undefined ? 0 : val) * this.left = (left===undefined ? null : left) * this.right = (right===undefined ? null : right) * } */ /** * @param {TreeNode} root * @return {boolean} */ var isSymmetric = function (root) { if (!root) return true let queue = [root.left, root.right] while (queue.length) { let l = queue.shift() let r = queue.shift() if (!l && !r) continue else if (!l || !r) return false else if (l.val !== r.val) return false queue.push(l.left) queue.push(r.right) queue.push(l.right) queue.push(r.left) } return true };
4. 二叉树的最大深度
题目:
给定一个二叉树 root ,返回其最大深度。
二叉树的 最大深度 是指从根节点到最远叶子节点的最长路径上的节点数。
思路:
二叉树的最大深度,即为二叉树根节点的高度。故,采用递归法,求二叉树根节点的高度即可。
- 确定递归函数的参数为当前遍历节点,返回值为当前遍历节点的高度
- 确定终止条件为当前遍历节点为空
- 确定单层递归的逻辑:
- 递归求取当前遍历节点的左子树的高度
- 递归求取当前遍历节点的右子树的高度
代码:
/**
* Definition for a binary tree node.
* function TreeNode(val, left, right) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
*/
/**
* @param {TreeNode} root
* @return {number}
*/
var maxDepth = function (root) {
return getHeight(root)
};
var getHeight = function (root) {
if (!root) return 0
let l = getHeight(root.left)
let r = getHeight(root.right)
return 1 + (l > r ? l : r)
}
5. 二叉树的最小深度
题目:
给定一个二叉树,找出其最小深度。
最小深度是从根节点到最近叶子节点的最短路径上的节点数量。
说明:叶子节点是指没有子节点的节点。
思路:
二叉树的最小深度,即为二叉树根节点到叶子节点的最小距离。故,采用递归法,还是求高度的过程。(和上题思路相似,但要对左右子树一个为空一个非空的情况单独讨论)
- 确定递归函数的参数为当前遍历节点,返回值为当前遍历节点到叶子节点的最小距离
- 确定终止条件为当前遍历节点为空或当前遍历节点的左右节点均空
- 确定单层递归的逻辑:
- 左子树非空则递归求取当前遍历节点的左子树节点到叶子节点的最小距离
- 右子树非空则递归求取当前遍历节点的右子树节点到叶子节点的最小距离
代码:
/**
* Definition for a binary tree node.
* function TreeNode(val, left, right) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
*/
/**
* @param {TreeNode} root
* @return {number}
*/
var minDepth = function (root) {
if (!root) return 0
if (!root.left && !root.right) return 1
if (!root.left) return 1 + minDepth(root.right);
if (!root.right) return 1 + minDepth(root.left);
let l = minDepth(root.left)
let r = minDepth(root.right)
return 1 + (l < r ? l : r)
};
6. 完全二叉树的节点个数
题目:
给你一棵 完全二叉树 的根节点 root ,求出该树的节点个数。
完全二叉树 的定义如下:在完全二叉树中,除了最底层节点可能没填满外,其余每层节点数都达到最大值,并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h 层,则该层包含 1~ 2h 个节点。
思路:
-
普通二叉树解法
直接遍历二叉树并进行计数即可。
-
完全二叉树解法
完全二叉树的定义:
利用完全二叉树的性质进行求解:
- 满二叉树——直接用 2^树深度 - 1 计算
- 最后一层叶子节点没有满——分别递归左右子树直至子树为满二叉树,然后按照上述1计算。
判断一个左子树或者右子树是不是满二叉树:
在完全二叉树中,如果递归向左遍历的深度等于递归向右遍历的深度,那么其就是满二叉树。
故:
- 若根节点为空,则直接返回 0
- 记录递归向左遍历的深度,记录递归向右遍历的深度
- 对比二者深度,若相同,则返回 2^左(右)深度 - 1 ;若不同,则分别递归计算其左右子树的节点个数,返回二者之和再加 1
代码:
-
普通二叉树解法
/** * Definition for a binary tree node. * function TreeNode(val, left, right) { * this.val = (val===undefined ? 0 : val) * this.left = (left===undefined ? null : left) * this.right = (right===undefined ? null : right) * } */ /** * @param {TreeNode} root * @return {number} */ var countNodes = function (root) { if (!root) return 0 return countNodes(root.left) + countNodes(root.right) + 1 }; -
完全二叉树解法
/** * Definition for a binary tree node. * function TreeNode(val, left, right) { * this.val = (val===undefined ? 0 : val) * this.left = (left===undefined ? null : left) * this.right = (right===undefined ? null : right) * } */ /** * @param {TreeNode} root * @return {number} */ var countNodes = function (root) { if (!root) return 0 let l = root.left, r = root.right let ln = 1, rn = 1 while (l) { l = l.left ln++ } while (r) { r = r.right rn++ } if (ln === rn) return 2 ** ln - 1 return countNodes(root.left) + countNodes(root.right) + 1 };