编译原理-上下文无关文法
CFG基本概念
符号串集合!
CFG可以表示所有正则表达式的所能表达文法集合,反过来不成立
CFG设计
可以结合正则表达式设计,思路类似。
-
最基本的一个例子:L={abb2n∣n≥0}
S→b|aSbb
-
设计接受语言{aibjakbl∣i+j=k+l,i,j,k,l>=0}的上下文无关文法。
S→aSb | A | B | M
A→aAa | M
B→bBb | M
M→bMa | e
思路:两边对称,先构造中间,再对称的加a或b。特别注意,A,B只涵盖了“一边的情况,所以”S→aSb“是必须的。
-
设计接受C++数组声明语句的上下文无关文法,其中数组元素类型限定为int、char及它们的指针,数组维数可以是任意维。
D→T id M ;
T→int | char | T*
M→M [num] | [num]
注意:指针也可以套任意个
-
形如xy(x≠y)的01串
S→AB∣BA
A→XAX∣0 ( A 是奇数长度, 中间为 0 的串)
B→XBX∣1 ( B 是奇数长度, 中间为 1 的串)
X→0∣1
-
接受语言 {aibjak∣j=i+k,i>=0,k>=0} 的上下文无关文法。 答:
S→ABA→aAb∣εB→bBa∣ε
练习:
-
{0i1j0k∣j=2i+k}
仿照最后一个题容易得到答案
-
无法写成 xx 形式的 01 串
仿照倒数第二个题,S→AB∣BA∣A∣B∣ε
NFA和CFG转换
一一对应即可,非常简单
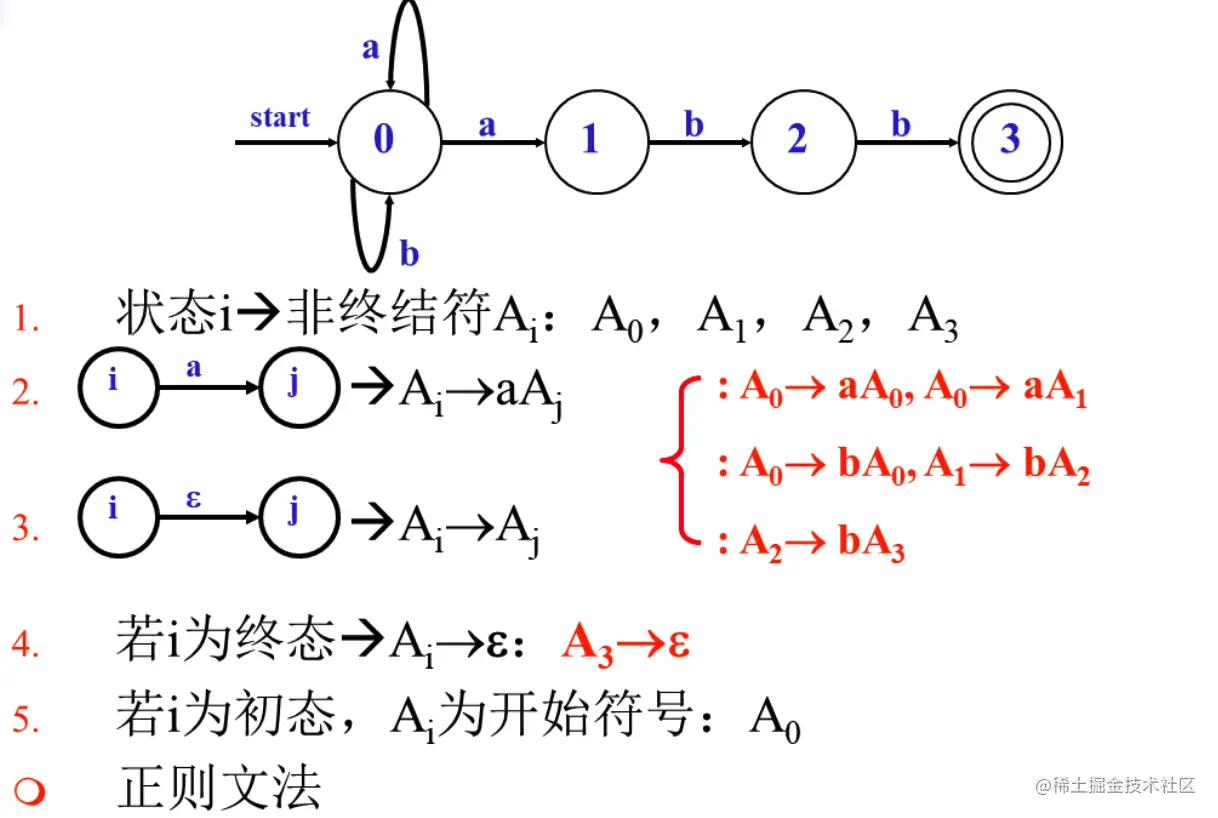
注意别忘了终态的规则(替换空串)
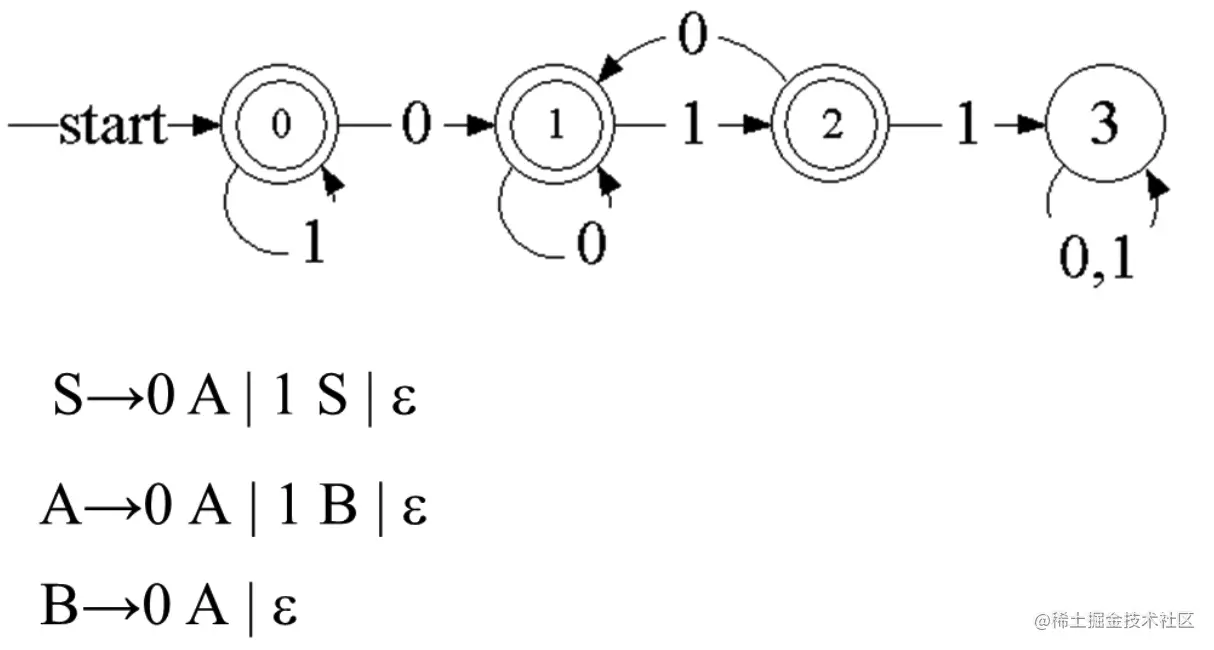
“不包含子串011的01串,3显然不需要包含进CFG”
CFG修改
消除二义性
消除二义性没有固定的套路,建立在对文法理解的基础上。

消除左递归
消除直接左递归很简单,在龙书第二章有所讲述。下面一个消除间接左递归的例子:

消除空字
消除空字需要注意的一点时一定要替换“干净”,即所有与含有空字的非终结符文法定义相关的条目都要考虑并替换
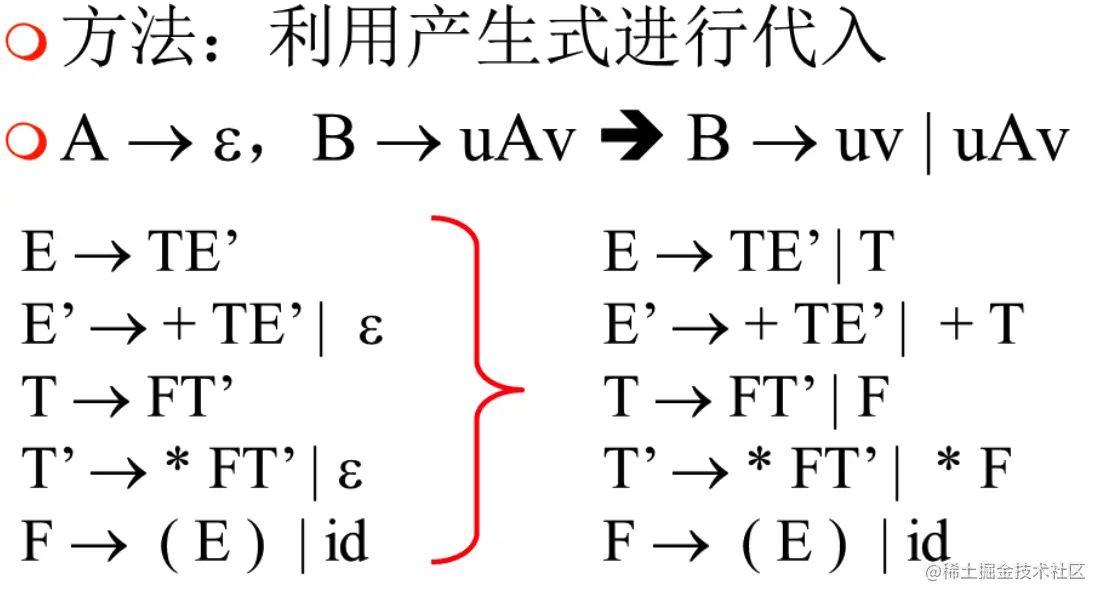
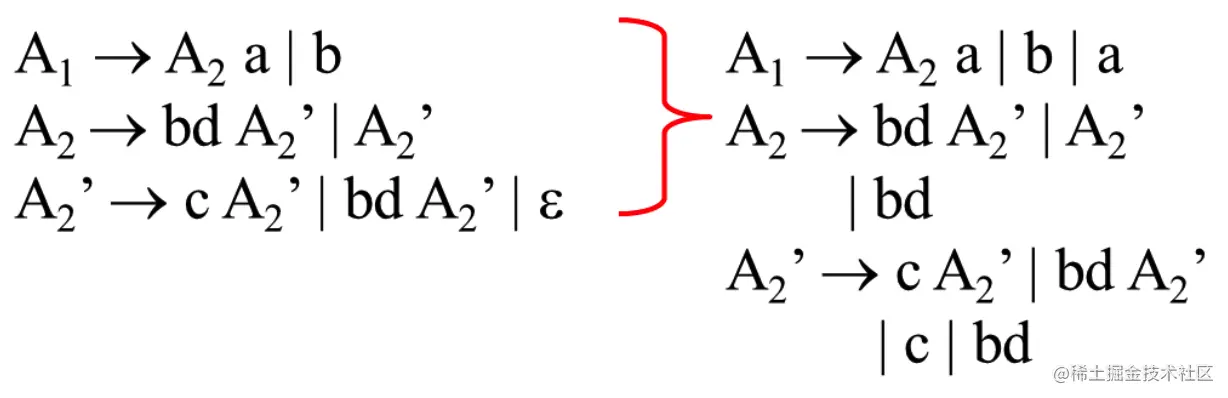
消除回路

左公因子提取
A→αβ1∣αβ2
改写为:
A→αA′
A′→β1∣β2
例子:
S→iEtS∣iEtSeS∣a
E→b
i → if, t→ then, e → else, E → 表达式, S → 语句
改写为:
S→iEtSS ' | a
S′→eS∣ε
E→b
CFG无法描述的语言结构
(重在理解)
例1: L1={wcw∣w∈(a∣b)∗}
检查标识符(w)必须在使用之前定义
语义分析阶段才能完成的事情
例2: L2={anbmcndm∣n⩾1 且 m⩾1}
检查函数的形参 (声明) 与实参 (调用)的数目是否匹配
语法定义一般不考虑参数数目
例3: L3={anbncn∣n≥0}
排版软件, 文本加下划线: n 个字符, n 个退格, n 个下划线
anbn容易描述(S→aSb)
另一种方式: 字符一退格一下划线三元 组序列, (abc)∗就可以描述了
可以描述的类似文法:
L1′={wcwRw∈(a∣b)∗,wR 为w的反转 }
S→aSa∣bSb∣c
L2′={anbmcmdn∣n⩾1 且 m⩾1}
和考试题类似,中心对称的,先处理中间
S→aSd∣aAdA→bAc∣bc
L2′′={anbncmdm∣n⩾1 且 m⩾1}
轴对称的,先处理两边
S→ABA→aAb∣abB→cBd∣cd
L3′={anbn∣n≥1}
S→aSb∣ab
PS:证明L3′不能用正则表达式表示
可以考虑证明它不能使用DFA进行表示。证明的关键就是定义”DF“(确定,有穷):
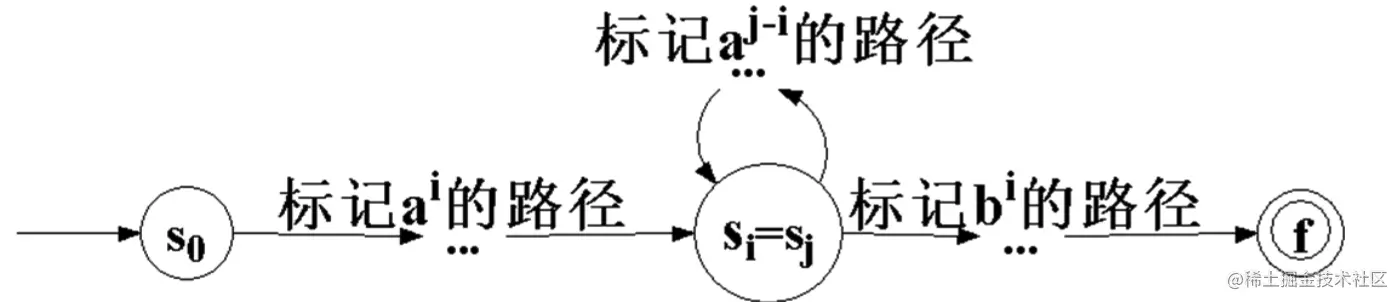
假定存在DFA D接受 L3′, 其状态数为 k(有穷)。 设状态 s0, s1,…,sk 为读入 ε,a,aa,…,ak 后的状态 ⇒si 为读入 i 个 a 达到的状态 (0⩽i⩽k)
总状态数 k→s0, s1,…,sk 中至少有两个相同状态, 不妨设为 si、sj,i<j
aibi∈L3→⇒si(sj) 到终态路径标记为 bi
→ 初态 → 终态还有标为 aibi 的路径 →D 接受 aibi, 与”D(确定)“矛盾!