Leecode Hot100 刷题笔记本-栈（C++版）

• 42. 接雨水 困难
• 84. 柱状图中最大的矩形 困难
• 394. 字符串解码 中等
• 739. 每日温度 中等

42. 接雨水

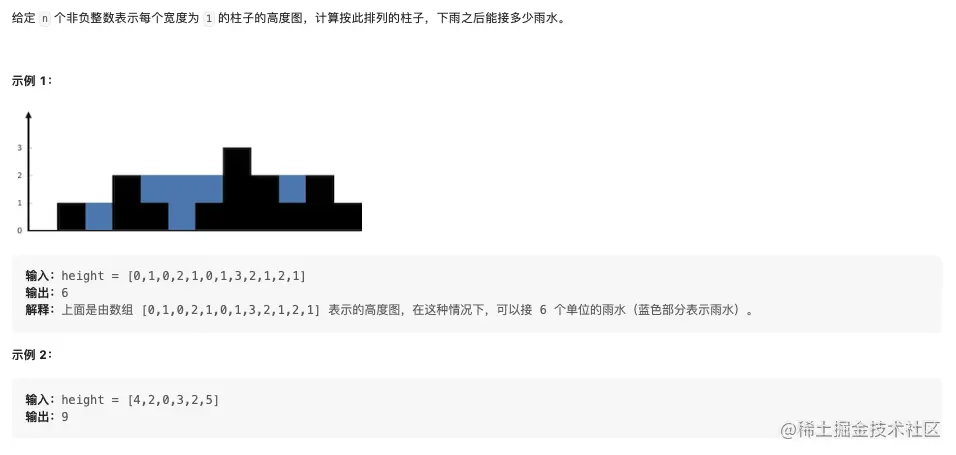
解法1: 单调栈

• 维护单调递减栈 栈中存放index

class Solution {
public:
    int trap(vector<int>& height) {
        int ans = 0;
        stack<int> stk;
        int n = height.size();
        for (int i = 0; i < n; ++i) {
            while (!stk.empty() && height[i] > height[stk.top()]) {
                int top = stk.top();
                stk.pop();
                if (stk.empty()) {
                    break;
                }
                int left = stk.top();
                int currWidth = i - left - 1;
                int currHeight = min(height[left], height[i]) - height[top];
                ans += currWidth * currHeight;
            }
            stk.push(i);
        }
        return ans;
    }
};

• 时间复杂度:O(N), 其中 n 是数组 height 的长度。从 0 到 n−1 的每个下标最多只会入栈和出栈各一次
• 空间复杂度:O(N), 空间复杂度主要取决于栈空间，栈的大小不会超过 n

解法2: 双指针

• 维护两个变量leftMax和rightMax

class Solution {
public:
    int trap(vector<int>& height) {
        int ans = 0;
        int left = 0, right = height.size() - 1;
        int leftMax = 0, rightMax = 0;
        while (left < right) {
            leftMax = max(leftMax, height[left]);
            rightMax = max(rightMax, height[right]);
            if (height[left] < height[right]) {
                ans += leftMax - height[left];
                ++left;
            } else {
                ans += rightMax - height[right];
                --right;
            }
        }
        return ans;
    }
};

• 时间复杂度:O(N), 其中 n 是数组 height 的长度。从 0 到 n−1 的每个下标最多只会入栈和出栈各一次
• 空间复杂度:O(1), 空间复杂度主要取决于栈空间，栈的大小不会超过 n 84. 柱状图中最大的矩形

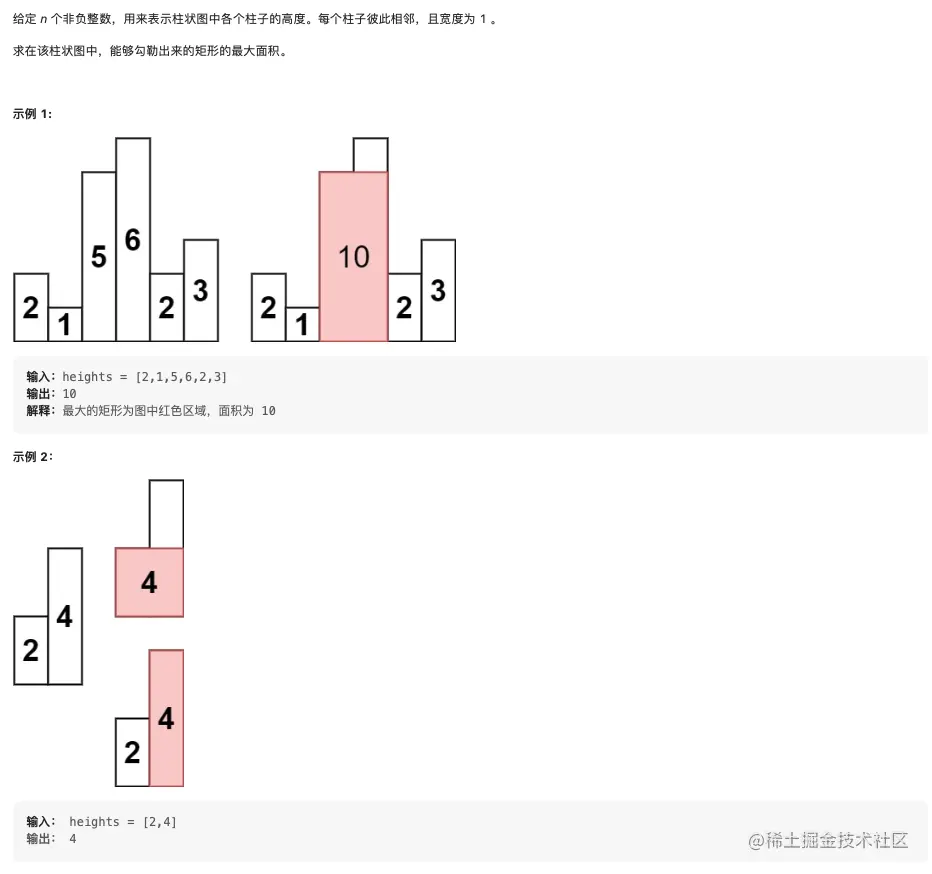
解法1: 单调栈

• for循环数组依次入栈出栈, 入栈的元素是数字的index, 当即将入栈的节点会破坏栈的单调性的时候, 出栈来保证栈的单调性
• 栈单调递减
• 维护最大面积变量ans = arr[i]* (right[i] - left[i] - 1)
• left[0] = -1

class Solution {
public:
    int largestRectangleArea(vector<int>& heights) {
        int n = heights.size();
        vector<int> left(n), right(n, n);
        
        stack<int> mono_stack;
        for (int i = 0; i < n; ++i) {
            while (!mono_stack.empty() && heights[mono_stack.top()] >= heights[i]) {
                right[mono_stack.top()] = i;
                mono_stack.pop();
            }
            left[i] = (mono_stack.empty() ? -1 : mono_stack.top());
            mono_stack.push(i);
        }
        
        int ans = 0;
        for (int i = 0; i < n; ++i) {
            ans = max(ans, (right[i] - left[i] - 1) * heights[i]);
        }
        return ans;
    }
};

• 时间复杂度:O(N), 其中 n 是数组 height 的长度。从 0 到 n−1 的每个下标最多只会入栈和出栈各一次
• 空间复杂度:O(N), 空间复杂度主要取决于栈空间，栈的大小不会超过 n

394. 字符串解码

解法1: 辅助栈法

string decodeString(string s) {
	//两个栈分别压int res和用pair
	stack<pair<int, string>> sta;
	int num = 0; string res = "";
	//循环检查字符串
	for (int i = 0; i < s.size(); i++) {
		//遇到数字则存入num
		if (s[i] >= '0'&&s[i] <= '9') {
			num *= 10;
			num += (s[i] - '0');//这里括号是否需要
		}
		else if (s[i] == '[') {//遇到[压栈数字和字符串，置零置空
			sta.push(make_pair(num, res));
			num = 0;
			res = "";
		}
		else if (s[i] == ']') {//遇到]出栈数字和字符串，组装
			int n = sta.top().first;//n指示的是res的循环次数，不是a的
			string a = sta.top().second;
			sta.pop();
			for (int i = 0; i < n; i++)  a = a + res; //循环n次
			res = a;
		}
		else {//遇到字符存入字符
			res += s[i];
		}		
	}
	return res;
}

• 时间复杂度:O(N)
• 空间复杂度:O(N)

解法1: 递归法

• 当 s[i] == ']' 时，返回当前括号内记录的 res 字符串与 ] 的索引 i （更新上层递归指针位置）
• 当 s[i] == '[' 时，开启新一层递归，记录此 [...] 内字符串 tmp 和递归后的最新索引 i，并执行 res + multi * tmp 拼接字符串。遍历完毕后返回 res

class Solution {
public:
    string src; 
    size_t ptr;

    int getDigits() {
        int ret = 0;
        while (ptr < src.size() && isdigit(src[ptr])) {
            ret = ret * 10 + src[ptr++] - '0';
        }
        return ret;
    }

    string getString() {
        if (ptr == src.size() || src[ptr] == ']') {
            // String -> EPS
            return "";
        }

        char cur = src[ptr]; int repTime = 1;
        string ret;

        if (isdigit(cur)) {
            // String -> Digits [ String ] String
            // 解析 Digits
            repTime = getDigits(); 
            // 过滤左括号
            ++ptr;
            // 解析 String
            string str = getString(); 
            // 过滤右括号
            ++ptr;
            // 构造字符串
            while (repTime--) ret += str; 
        } else if (isalpha(cur)) {
            // String -> Char String
            // 解析 Char
            ret = string(1, src[ptr++]);
        }
        
        return ret + getString();
    }

    string decodeString(string s) {
        src = s;
        ptr = 0;
        return getString();
    }
};

• 时间复杂度:O(S), S为字符串长度
• 空间复杂度:O(S)

739. 每日温度

解法1: 单调栈

• 维护一个存储下标的单调栈，从栈底到栈顶的下标对应的温度列表中的温度依次递减

class Solution {
public:
    vector<int> dailyTemperatures(vector<int>& temperatures) {
        int n = temperatures.size();
        vector<int> ans(n);
        stack<int> s;
        for (int i = 0; i < n; ++i) {
            while (!s.empty() && temperatures[i] > temperatures[s.top()]) {
                int previousIndex = s.top();
                ans[previousIndex] = i - previousIndex;
                s.pop();
            }
            s.push(i);
        }
        return ans;
    }
};

• 时间复杂度:O(N), N 是温度列表的长度
• 空间复杂度:O(N)