Leecode Hot100 刷题笔记本-二分查找（C++版）33. 搜索旋转排序数组中等 34. 在排序数组中查找元

33. 搜索旋转排序数组

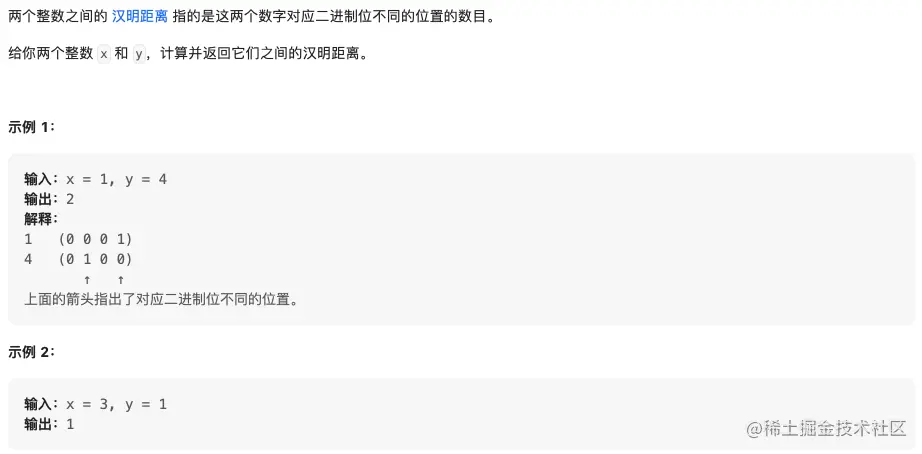
Screen Shot 2023-08-13 at 6.27.34 PM.png

解法1: 二分查找

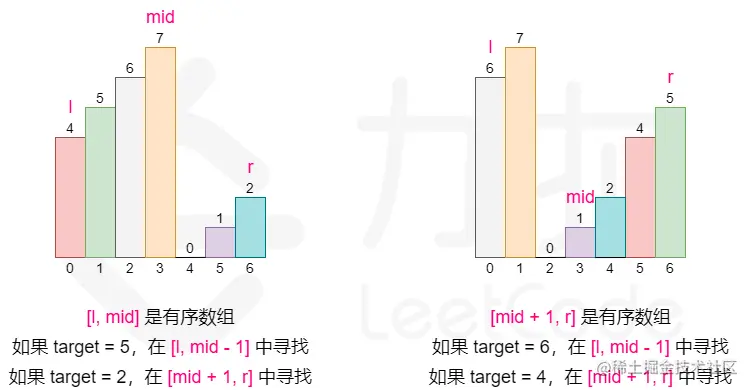
Screen Shot 2023-08-14 at 10.47.37 AM.png

定理一：只有在顺序区间内才可以通过区间两端的数值判断target是否在其中。
定理二：判断顺序区间还是乱序区间，只需要对比 left 和 right 是否是顺序对即可，left <= right，顺序区间，否则乱序区间。
定理三：每次二分都会至少存在一个顺序区间。

class Solution {
public:
    int search(vector<int>& nums, int target) {
        int left = 0, right = nums.size() - 1;
        while (left <= right) {
            int mid = (left + right) >> 1;
            if (nums[mid] == target) return mid;
            if (nums[left] <= nums[mid]) {
                // left 到 mid 是顺序区间
                (target >= nums[left] && target < nums[mid]) ? right = mid - 1 : left = mid + 1;
            }
            else {
                // mid 到 right 是顺序区间
                (target > nums[mid] && target <= nums[right]) ? left = mid + 1 : right = mid - 1;
            }
        }
        return -1;
    }
};

时间复杂度: O(logn)，其中 n 为 nums 数组的大小。整个算法时间复杂度即为二分查找的时间复杂度 O(logn)。
空间复杂度: O(1) 。我们只需要常数级别的空间存放变量

34. 在排序数组中查找元素的第一个和最后一个位置

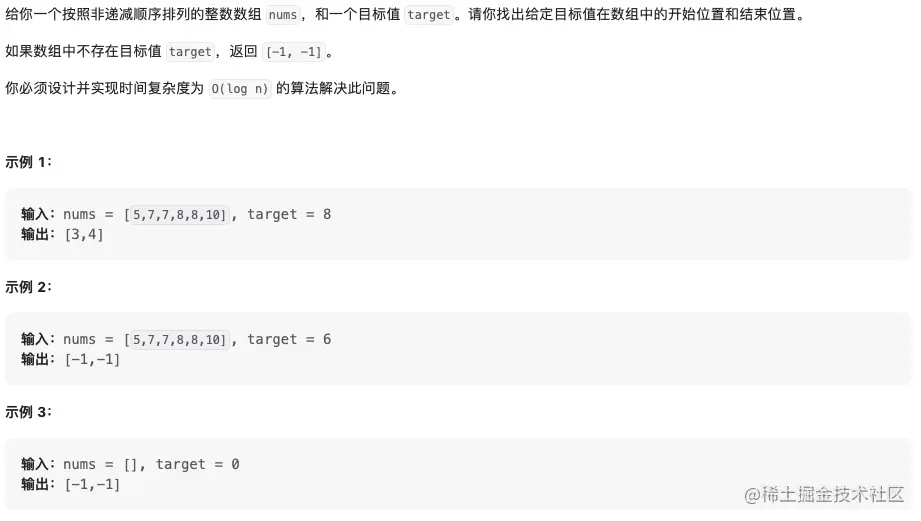
Screen Shot 2023-08-14 at 11.03.33 AM.png

分开查找第一个等于target的和最后一个等于target的

class Solution {
public:
    vector<int> searchRange(vector<int>& nums, int target) {
        int left=0, right=nums.size()-1, middle, ans_left=-1, ans_right=-1;
        // 查找左边界
        while(left<=right){
            middle = left + (right - left) / 2;
            if(nums[middle]==target){
                ans_left = middle;
                right = middle - 1;//因为是左边界，所以要看看左边是不是还有目标值存在
            }
            else if(nums[middle]<target)
                left = middle + 1;
            else
                right = middle - 1;
        }
        // 查找右边界
        left=0;
        right=nums.size()-1;
        while(left<=right){
            middle = left + (right - left) / 2;
            if(nums[middle]==target){
                ans_right = middle;
                left = middle + 1;//因为是右边界，所以要看看右边是不是还有目标值存在
            }
            else if(nums[middle]<target)
                left = middle + 1;
            else
                right = middle - 1;
        }
        return {ans_left, ans_right};
    }
};

时间复杂度: O(logn)，其中 n 为数组的大小。整个算法时间复杂度即为二分查找的时间复杂度 O(logn)。
空间复杂度: O(1) 。我们只需要常数级别的空间存放变量

240. 搜索二维矩阵 II

Screen Shot 2023-08-14 at 4.06.05 PM.png

解法1: 直接查找

我们直接遍历整个矩阵 matrix，判断 target 是否出现即可

class Solution {
public:
    bool searchMatrix(vector<vector<int>>& matrix, int target) {
        for (const auto& row: matrix) {
            for (int element: row) {
                if (element == target) {
                    return true;
                }
            }
        }
        return false;
    }
};

时间复杂度: O(mn)
空间复杂度: O(1)

解法2: 二分查找

lower_bound(begin, end, value)
在从小到大的排好序的数组中，在数组的 [begin, end) 区间中二分查找第一个大于value的数，找到返回该数字的地址，没找到则返回end

class Solution {
public:
    bool searchMatrix(vector<vector<int>>& matrix, int target) {
        for (const auto& row: matrix) {
            auto it = lower_bound(row.begin(), row.end(), target);
            if (it != row.end() && *it == target) {
                return true;
            }
        }
        return false;
    }
};

时间复杂度: O(mlogn)。对一行使用二分查找的时间复杂度为 O(log⁡n)，最多需要进行 m 次二分查找
空间复杂度: O(1)

解法3: Z字形查找

从右上角开始（0, n-1）进行搜索
如果 matrix[x,y]=target 说明搜索完成
如果 matrix[x,y]>target，由于每一列的元素都是升序排列的，那么在当前的搜索矩阵中，所有位于第 y 列的元素都是严格大于 target 的，因此我们可以将它们全部忽略，即将 y 减少 1
如果 matrix[x,y]<target，由于每一行的元素都是升序排列的，那么在当前的搜索矩阵中，所有位于第 x 行的元素都是严格小于 target 的，因此我们可以将它们全部忽略，即将 x 增加 1

class Solution {
public:
    bool searchMatrix(vector<vector<int>>& matrix, int target) {
        int m = matrix.size(), n = matrix[0].size();
        int x = 0, y = n - 1;
        while (x < m && y >= 0) {
            if (matrix[x][y] == target) {
                return true;
            }
            if (matrix[x][y] > target) {
                --y;
            }
            else {
                ++x;
            }
        }
        return false;
    }
};

时间复杂度: O(m+n)。在搜索的过程中，如果我们没有找到 target，那么我们要么将 y 减少 1，要么将 x 增加 1。由于 (x,y) 的初始值分别为 (0,n−1)，因此 y 最多能被减少 n 次，x 最多能被增加 m 次，总搜索次数为 m+n。在这之后，x 和 y 就会超出矩阵的边界
空间复杂度: O(1)

287. 寻找重复数

Screen Shot 2023-08-14 at 11.26.57 AM.png

解法1: 原地交换

若 nums[nums[i]]=nums[i] ：代表索引 nums[i] 处和索引 i 处的元素值都为 nums[i] ，即找到一组重复值，返回此值 nums[i]

class Solution {
public:
   int findDuplicate(vector<int>& nums) {
   while(nums[0]!=nums[nums[0]])swap(nums[0],nums[nums[0]]);
   return nums[nums[0]];
  }
};

时间复杂度: 遍历数组使用 O(N) ，每轮遍历的判断和交换操作使用 O(1)
空间复杂度: O(1), 使用常数复杂度的额外空间

解法2: 哈希表

class Solution {
public:
    int findDuplicate(vector<int>& nums) {
        unordered_map<int, bool> map;
        for(int num : nums) {
            if(map[num]) return num;
            map[num] = true;
        }
        return -1;
    }
};

时间复杂度: 遍历数组使用 O(N) ，每轮遍历的判断和交换操作使用 O(1)
空间复杂度: HashSet 占用 O(N) 大小的额外空间

解法3: 二分查找法

mid = (1 + n) / 2，重复数要么落在[1, mid]，要么落在[mid + 1, n]
遍历原数组，统计 <= mid 的元素个数，记为 k
如果k > mid，说明有超过 mid 个数落在[1, mid]，但该区间只有 mid 个“坑”，说明重复的数落在[1, mid]
相反，如果k <= mid，则说明重复数落在[mid + 1, n]
对重复数所在的区间继续二分，直到区间闭合，重复数就找到了

class Solution {
public:
    int findDuplicate(vector<int>& nums) {
        int n = nums.size();
        int l = 1, r = n - 1, ans = -1;
        while (l <= r) {
            int mid = (l + r) >> 1;
            int cnt = 0;
            for (int i = 0; i < n; ++i) {
                cnt += nums[i] <= mid;
            }
            if (cnt <= mid) {
                l = mid + 1;
            } else {
                r = mid - 1;
                ans = mid;
            }
        }
        return ans;
    }
};

时间复杂度: O(nlogn). 其中 n 为 nums 数组的长度。二分查找最多需要二分 O(log⁡n) 次，每次判断的时候需要O(n) 遍历 nums 数组求解小于等于 mid 的数的个数，因此总时间复杂度为 O(nlog⁡n)
空间复杂度: O(1). 我们只需要常数空间存放若干变量

解法4: 快慢指针（检查链表里面是否有环）

class Solution {
public:
    int findDuplicate(vector<int>& nums) {
        int slow = 0, fast = 0;
        do {
            slow = nums[slow];
            fast = nums[nums[fast]];
        } while (slow != fast);
        slow = 0;
        while (slow != fast) {
            slow = nums[slow];
            fast = nums[fast];
        }
        return slow;
    }
};

时间复杂度: O(n)。「Floyd 判圈算法」时间复杂度为线性的时间复杂度。
空间复杂度: O(1). 我们只需要常数空间存放若干变量