算法套路十五——动态规划求解最长公共子序列LCS
算法示例:LeetCode1143. 最长公共子序列
给定两个字符串 text1 和 text2,返回这两个字符串的最长 公共子序列 的长度。如果不存在 公共子序列 ,返回 0 。 一个字符串的 子序列 是指这样一个新的字符串:它是由原字符串在不改变字符的相对顺序的情况下删除某些字符(也可以不删除任何字符)后组成的新字符串。 例如,"ace" 是 "abcde" 的子序列,但 "aec" 不是 "abcde" 的子序列。 两个字符串的 公共子序列 是这两个字符串所共同拥有的子序列。
二维数组动态规划
-
定义:设 表示序列 的前 个字符和序列 的前 个字符的最长公共子序列长度。
-
初始化:当 或 时,,因为一个空序列和另一个序列的任何子序列都没有公共部分。
-
状态转移方程:对于序列 中的第 个字符和序列 中的第 个字符,有两种情况:
- 如果 ,则当前字符可以包含在最长公共子序列中,因此有 ;
- 如果 ,则当前字符不能同时出现在最长公共子序列中,因此取两种情况的较大值:去掉 后与序列 的前 个字符的最长公共子序列长度,或者与序列 的前 个字符去掉 后的最长公共子序列长度。即 。
-
状态转移方程及dp数组初始化如下所示:
0, & i=0, j>0 \\
0, & i>0, j=0 \\
dp[i][j]+1, & i,j>0,X_i=Y_j \\
\max(dp[i+1][j], dp[i][j+1]), & i,j>0,X_i \neq Y_i
\end{cases}$$
5. 返回值
最终,$dp[m][n]$ 即为序列 $X$ 和序列 $Y$ 的最长公共子序列长度,其中 $m$ 和 $n$ 分别为序列 $X$ 和 $Y$ 的长度。
```python
class Solution:
def longestCommonSubsequence(self, text1: str, text2: str) -> int:
n, m = len(text1), len(text2)
dp = [[0]*(m+1) for _ in range(n + 1)]
for i in range(n):
for j in range(m):
if text1[i]==text2[j]:
dp[i+1][j+1]=dp[i][j]+1
else:
dp[i+1][j+1]=max(dp[i][j + 1], dp[i + 1][j])
return dp[n][m]
```
### 空间优化为一维数组
本题的状态转移数组需要考虑$dp[i][j]、dp[i][j + 1]、dp[i + 1][j]$三个状态,分别位于二维数组中的左边,上边与左上,对于左上的状态即dp[i][j],在二维矩阵中,更新第 i+1 行第 j+1 列的元素需要用到第 i 行第 j 列和第 i 行第 j+1 列的元素。而在一维数组中,如果直接覆盖 dp[j+1] 的值,则第 i 行第 j 列的元素就会被新值所覆盖,从而无法在计算第 i+1 行中的其他元素时继续使用。因此,我们需要在更新 dp[j+1] 的同时,记录旧值并存储到 temp 变量中,以便在下一轮迭代中使用。
```python
class Solution:
def longestCommonSubsequence(self, text1: str, text2: str) -> int:
n, m = len(text1), len(text2)
dp = [0]*(m+1)
for i in range(n):
temp = dp[0]
for j in range(m):
if text1[i]==text2[j]:
# dp[j+1] 表示左上角的值,dp[j+1] = temp + 1 表示将左上角的值加一,赋值给当前单元格;
# 同时将更新前的 dp[j+1] 赋值给 temp,以便下次迭代中计算下一个单元格所需的左上角的值。
dp[j+1], temp = temp+1, dp[j+1]
else:
dp[j+1], temp = max(dp[j], dp[j+1]), dp[j+1]
return dp[m]
```
## 算法练习一:[LeetCode583. 两个字符串的删除操作](https://leetcode.cn/problems/delete-operation-for-two-strings/)
> 给定两个单词 word1 和 word2 ,返回使得 word1 和 word2 相同所需的最小步数。
每步 可以删除任意一个字符串中的一个字符。

如上图所示,本题关键在于两字符串的求最长公共子序列LCS,求出之后直接可以得出答案为len(word1)+len(word2)-2*len(lcs),因此我们直接利用示例函数longestCommonSubsequence()求出len(lcs)
```go
func minDistance(word1 string, word2 string) int {
lcsLen := one_dimensional_longestCommonSubsequence(word1, word2)
return len(word1) + len(word2) - 2*lcsLen
}
func one_dimensional_longestCommonSubsequence(text1 string, text2 string) int {
n, m := len(text1), len(text2)
dp := make([]int, m+1)
for i := 0; i < n; i++ {
temp := dp[0]
for j := 0; j < m; j++ {
if text1[i] == text2[j] {
// dp[j+1] 表示左上角的值,dp[j+1] = temp + 1 表示将左上角的值加一,
// 赋值给当前单元格;同时将更新前的 dp[j+1] 赋值给 temp,
// 以便下次迭代中计算下一个单元格所需的左上角的值。
dp[j+1], temp = temp+1, dp[j+1]
} else {
dp[j+1], temp = max(dp[j], dp[j+1]), dp[j+1]
}
}
}
return dp[m]
}
func max(a, b int) int { if a > b {return a}; return b}
```
## 算法练习二:[LeetCode712. 两个字符串的最小ASCII删除和](https://leetcode.cn/problems/minimum-ascii-delete-sum-for-two-strings/)
> 给定两个字符串s1 和 s2,返回 使两个字符串相等所需删除字符的 ASCII 值的最小和 。
](https://img-blog.csdnimg.cn/4872c89a5df747d38dd19bb4a4a8a64e.png)
该题与上题相似,唯一区别在于所求的为公共子序列的最大AscII值,因此我们可以修改状态转移方程如下所示即可求出:
$$dp[i+1][j+1] = \begin{cases}
0, & i=0, j>0 \\
0, & i>0, j=0 \\
dp[i][j]+X_i的ASCII值, & i,j>0,X_i=Y_j \\
\max(dp[i+1][j], dp[i][j+1]), & i,j>0,X_i \neq Y_i
\end{cases}$$
```go
func minimumDeleteSum(s1 string, s2 string) int {
lcaAsCII:=one_dimensional_largestAsCII_common_subsequence(s1,s2)
return sumAsCII(s1)+sumAsCII(s2)-2*lcaAsCII
}
func one_dimensional_largestAsCII_common_subsequence(text1 string, text2 string) int {
n, m := len(text1), len(text2)
dp := make([]int, m+1)
for i := 0; i < n; i++ {
temp := dp[0]
for j := 0; j < m; j++ {
if text1[i] == text2[j] {
#唯一区别temp+1修改为temp+int(text1[i])
dp[j+1], temp = temp+int(text1[i]), dp[j+1]
} else {
dp[j+1], temp = max(dp[j], dp[j+1]), dp[j+1]
}
}
}
return dp[m]
}
func max(a, b int) int { if a > b {return a}; return b}
func sumAsCII(str string)(sum int){
for _,c:=range str{
sum+=int(c)
}
return sum
}
```
## 算法进阶一:[LeetCode1458. 两个子序列的最大点积](https://leetcode.cn/problems/max-dot-product-of-two-subsequences/)
> 给你两个数组 nums1 和 nums2 。
请你返回 nums1 和 nums2 中两个长度相同的 非空 子序列的最大点积。
数组的非空子序列是通过删除原数组中某些元素(可能一个也不删除)后剩余数字组成的序列,但不能改变数字间相对顺序。比方说,[2,3,5] 是 [1,2,3,4,5] 的一个子序列而 [1,5,3] 不是。
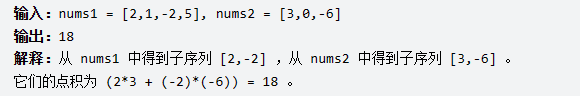
### 二维数组动态规划
在LCS问题中,当text1[i]和text2[j]相等时,可以通过将这个相同的元素加入最长公共子序列来使最终结果+1或者ASCII值。但在最大点积问题中,`若nums1[i]和nums2[j]的积大于0,表明它们的符号相同,这只是可能会对最终结果产生正影响,但并不能确定它们一定需要配对,通过比较不同需求下的dp数组之间的大小关系,才能得出最大的点积值`,如下所示:
> 如nums1 = [5, -2, 3],nums2 = [-4, -1, 2]$$可得dp[1][1]=0且num1[1]*nums2[1]=(-2)*(-1)=2,但此时还有dp[1][2]=0,dp[2][1]=(-2)*(-4)=8$$在这种情况下nums1[i]*nums2[j]虽然大于0,但我们仍需要考虑dp[2][1]的值, 故此时$$dp[2][2]=max(dp[2][1],dp[1][2],dp[1][1]+num1[1]*nums2[1]]=8$$
首先定义一个二维数组 dp,其中 dp[i][j] 表示 nums1 前 i 个数和 nums2 前 j 个数组成的两个子序列的最大点积。
状态转移方程如下:$$dp[i][j] = max(dp[i-1][j-1] + nums1[i-1]*nums2[j-1],dp[i][j-1],dp[i-1][j])$$
dp[i-1][j-1] +nums1[i-1]*nums2[j-1]表示将当前最后一个元素从两个数组中取出做点积;dp[i][j-1] 和 dp[i-1][j] 分别表示不取 nums1[i-1] 和不取 nums2[j-1],只选取前面元素得到的最大点积。
```go
func maxDotProduct(nums1 []int, nums2 []int) int {
return two_dimensional_Max_dot_product(nums1,nums2)
}
func two_dimensional_Max_dot_product(nums1 []int, nums2 []int) int {
n, m := len(nums1), len(nums2)
dp := make([][]int, n+1)
for i := range dp {
dp[i] = make([]int, m+1)
}
ans:=math.MinInt
for i := 1; i <= n; i++ {
for j := 1; j <= m; j++ {
acc:=nums1[i-1]* nums2[j-1]
dp[i][j] = maxOfThree(dp[i-1][j-1]+acc , dp[i-1][j], dp[i][j-1])
ans=max(ans,acc)
}
}
if dp[n][m]==0{return ans}
return dp[n][m]
}
func maxOfThree(a, b, c int) int {
max := a
if b > max {max = b}
if c > max {max = c}
return max
}
func max(a, b int) int { if a > b {return a}; return b}
```
### 空间优化为一维数组
空间优化同LCS问题,需要使用temp记录,状态转移方程及初始数组无区别
```go
func maxDotProduct(nums1 []int, nums2 []int) int {
return one_dimensional_Max_dot_product(nums1,nums2)
}
func one_dimensional_Max_dot_product(nums1 []int, nums2 []int) int {
n, m := len(nums1), len(nums2)
dp := make([]int, m+1)
ans:=math.MinInt
for i := 0; i < n; i++ {
temp := dp[0]
for j := 0; j < m; j++ {
acc:=nums1[i]*nums2[j]
dp[j+1], temp =maxOfThree(temp+acc,dp[j],dp[j+1]),dp[j+1]
ans=max(ans,acc)
}
}
//如果dp[m]==0,说明ans即最大的乘积acc<=0,故可直接返回acc
if dp[m]==0{return ans}
return dp[m]
}
func maxOfThree(a, b, c int) int {
max := a
if b > max {max = b}
if c > max {max = c}
return max
}
func max(a, b int) int { if a > b {return a}; return b}
```
## 算法进阶二:[LeetCode97. 交错字符串](https://leetcode.cn/problems/interleaving-string/)
> 给定三个字符串 s1、s2、s3,请你帮忙验证 s3 是否是由 s1 和 s2 交错 组成的。
两个字符串 s 和 t 交错 的定义与过程如下,其中每个字符串都会被分割成若干 非空 子字符串:
s = s1 + s2 + ... + sn
t = t1 + t2 + ... + tm
|n - m| <= 1
交错 是 s1 + t1 + s2 + t2 + s3 + t3 + ... 或者 t1 + s1 + t2 + s2 + t3 + s3 + ...
注意:a + b 意味着字符串 a 和 b 连接。
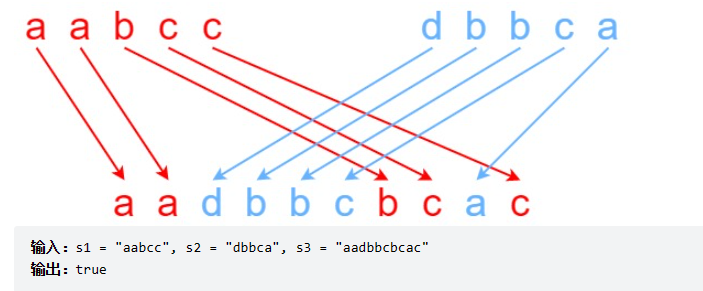
> 双指针法错在哪里?也许有同学看到这道题目的第一反应是使用双指针法解决这个问题,指针 p1一开始指向s1的头部,指针
> p2一开始指向s2的头部,指针 p3指向s3的头部,每次观察p1和p2指向的元素哪一个和p3指向的元素相等,相等则匹配并后移指针。
> 若判断s1 = bcc,s2 = bbca,s3 =bbcbcac时,当p3指向s3的b时,对于s1与s2都有b,因此此时仍需要分别记录p1指针前进与p2指针前进两种情况,需要分别判断每种情况是否能够满足字符串交错,因此不能使用单一的双指针法来解决。
### 递归+记忆化搜索
本题不是一般的LCS问题,对于状态转移方程不是很容易理解,因此我们首先采用递归+记忆化搜索的方法解决该问题。
我们可以定义一个递归函数 dfs(i, j, k),其中 s1、s2 和 s3 分别表示三个字符串,i、j 和 k 分别表示当前匹配到 s1、s2 和 s3 的哪个位置。
递归函数的基本思路如下:
1. 如果 i、j 和 k 都等于字符串的长度,说明 s3 可以由 s1 和 s2 交错组成,返回 True。
2. 如果 k 等于字符串 s3 的长度,但 i 或 j 不等于对应字符串的长度,说明 s3 不能由 s1 和 s2 交错组成,返回 False。
3. 如果 s1[i] 等于 s3[k],那么我们可以递归判断 s1[i+1:]、s2[j:] 和 s3[k+1:] 是否可以交错组成。如果可以,返回 True。
4. 如果 s2[j] 等于 s3[k],那么我们可以递归判断 s1[i:]、s2[j+1:] 和 s3[k+1:] 是否可以交错组成。如果可以,返回 True。
5. 如果 s1[i] 和 s2[j] 都不等于 s3[k],那么 s3 不能由 s1 和 s2 交错组成,返回 False。
```python
class Solution:
def isInterleave(self, s1: str, s2: str, s3: str) -> bool:
@cache
def dfs(i, j, k):
if i == len(s1) and j == len(s2) and k == len(s3):
return True
if k == len(s3) and (i != len(s1) or j != len(s2)):
return False
if i < len(s1) and s1[i] == s3[k] and dfs(i+1, j, k+1):
return True
if j < len(s2) and s2[j] == s3[k] and dfs(i, j+1, k+1):
return True
return False
return dfs(0, 0, 0)
```
### 二维数组动态规划
根据以上递归过程,我们可以得出动态规划的式子,
1. dp数组:dp[i][j] 表示 s1 的前 i 个字符和 s2 的前 j 个字符是否能够交错组成 s3 的前 i+j 个字符。
2. 初始化: dp[0][0] = True,因为空字符串可以组成空字符串。
3. 动态转移方程:
$dp[i][j] = \begin{cases}
true, & i=0, j=0 \\
dp[0][j-1] \text{ and } s2[j-1] = s3[j-1], & i=0, j \geq 1 \\
dp[i-1][0] \text{ and } s1[i-1] = s3[i-1], & i \geq 1, j=0 \\
(dp[i-1][j] \text{ and } s1[i-1] = s3[i+j-1]) \text{ or } (dp[i][j-1] \text{ and } s2[j-1] = s3[i+j-1]), & i \geq 1, j \geq 1
\end{cases}$
4. 返回值:最终的答案为 dp[n][m],其中 n 和 m 分别是 s1 和 s2 的长度。
```go
func isInterleave(s1 string, s2 string, s3 string) bool {
n,m:=len(s1),len(s2)
if n+ m != len(s3) {
return false
}
dp := make([][]bool, n+ 1)
for i := range dp {
dp[i] = make([]bool, m + 1)
}
dp[0][0] = true
for i := 1; i <= n; i++ {
dp[i][0] = dp[i-1][0] && s1[i-1] == s3[i-1]
}
for j := 1; j <= m; j++ {
dp[0][j] = dp[0][j-1] && s2[j-1] == s3[j-1]
}
for i := 1; i <= n; i++ {
for j := 1; j <= m; j++ {
/*if s1[i-1] == s3[i+j-1]{
dp[i][j] =dp[i][j] || dp[i-1][j]
}
if s2[j-1] == s3[i+j-1]{
dp[i][j] =dp[i][j] || dp[i][j-1]
}*/
dp[i][j] = (dp[i-1][j] && s1[i-1] == s3[i+j-1]) || (dp[i][j-1] && s2[j-1] == s3[i+j-1])
}
}
return dp[n][m]
}
```
### 空间优化
```go
func isInterleave(s1 string, s2 string, s3 string) bool {
n1, n2, n3 := len(s1), len(s2), len(s3)
if n1 + n2 != n3 {
return false
}
dp := make([]bool, n2 + 1)
dp[0] = true
for i := 0; i <= n1; i++ {
for j := 0; j <= n2; j++ {
if i == 0 && j > 0 {
dp[j] = dp[j-1] && (s2[j-1] == s3[i+j-1])
} else if i > 0 && j == 0 {
dp[j] = dp[j] && (s1[i-1] == s3[i+j-1])
} else if i > 0 && j > 0 {
dp[j] = (dp[j] && (s1[i-1] == s3[i+j-1])) ||
(dp[j-1] && (s2[j-1] == s3[i+j-1]))
}
}
}
return dp[n2]
}
```
## 算法进阶三:[LeetCode72. 编辑距离](https://leetcode.cn/problems/edit-distance/)
> 给你两个单词 word1 和 word2, 请返回将 word1 转换成 word2 所使用的最少操作数 。
你可以对一个单词进行如下三种操作:
插入一个字符
删除一个字符
替换一个字符

### 递归+记忆化搜索
1. 递归函数定义:递归函数 dfs 接受两个参数 i 和 j,分别表示 word1 和 word2 的索引。dfs 函数的返回值是将 word1 转换成 word2 所需的最少操作次数。在这个函数中,我们使用 Python 3 中的 functools.cache 装饰器来缓存递归函数的结果,避免重复计算。
2. 递归方程:
如果 i < 0,说明 word1 已经遍历完,此时需要插入 j+1 个字符才能匹配 word2,因此返回 j+1。
如果 j < 0,说明 word2 已经遍历完,此时需要插入 i+1 个字符才能匹配 word1,因此返回 i+1。
如果 word1[i] == word2[j],说明当前字符相等,不需要进行操作,递归到下一个字符,即 dfs(i-1, j-1)。
如果 word1[i] != word2[j],说明当前字符不相等,需要进行插入、删除或替换操作。具体来说:
- 插入操作:在 word1 中插入一个字符,使得 word1[i+1] == word2[j],此时需要递归到 dfs(i, j-1)。
- 删除操作:删除 word1 中的一个字符,使得 word1[i-1] == word2[j],此时需要递归到 dfs(i-1, j)。
- 替换操作:将 word1 中的一个字符替换成 word2 中的一个字符,使得 word1[i-1] == word2[j-1],此时需要递归到 dfs(i-1, j-1)。
- 在这三种操作中,取操作次数最少的一种,即 min(dfs(i-1, j), dfs(i, j-1), dfs(i-1, j-1)),然后加 1,即可得到将 word1 转换成 word2 所需的最少操作次数。
7. 边界条件:在递归函数中,我们需要判断 word1 和 word2 是否已经遍历完,如果是,则返回另一个字符串的长度加 1,因为此时需要插入字符来匹配另一个字符串。具体来说,如果 i < 0,则返回 j + 1;如果 j < 0,则返回 i + 1。
8. 所求值:我们需要调用递归函数,传入 word1 和 word2 的长度减 1 作为参数,返回最终的编辑距离。具体来说,我们需要返回 dfs(n - 1, m - 1),其中 n 和 m 分别是 word1 和 word2 的长度。
下面是递归过程的分情况解释:
```python
class Solution:
def minDistance(self, word1: str, word2: str) -> int:
n,m=len(word1),len(word2)
@cache
def dfs(i:int,j:int)->int:
if i<0:
return j+1
if j<0:
return i+1
if word1[i]==word2[j]:
return dfs(i-1,j-1)
else:
return min(dfs(i-1,j),dfs(i,j-1),dfs(i-1,j-1))+1
return dfs(n-1,m-1)
```
### 二维数组动态规划
根据以上递归过程,我们可以得出动态规划的式子
下面是编辑距离问题的动态规划解法:
1. 定义状态:dp[i][j] 表示将 word1 的前 i 个字符转换为 word2 的前 j 个字符所需的最少操作次数。
2. 初始化:当字符串长度为 0 时,相互转化不需要任何操作。因此dp[0][j]=j, dp[i][0]=i。
3. 转移方程:
- 当 word1[i] == word2[j] 时,此时不需要进行任何操作,所以dp[i][j] = dp[i-1][j-1]。
- 当 word1[i] != word2[j] 时,需要进行插入、删除、替换三种操作中的一种,取这三种操作中操作次数最少的一种,并加上 1,即可得到 dp[i][j]:
- 插入操作: dp[i][j] = dp[i][j-1] + 1
- 删除操作: dp[i][j] = dp[i-1][j] + 1
- 替换操作: dp[i][j] = dp[i-1][j-1] + 1
$$dp[i][j] = \begin{cases}
0, & i=0, j=0 \\
i, & i \geq 1, j=0 \\
j, & i=0, j \geq 1 \\
\begin{aligned}
& \min(dp[i-1][j], dp[i][j-1], dp[i-1][j-1]) + 1, \
& \quad \text word1[i-1] \neq word2[j-1]\\
& \quad dp[i-1][j-1]& \quad \text word1[i-1] = word2[j-1]\
\end{aligned}
\end{cases}$$
4. 边界情况:当 i = 0 时,表示 word1 已经遍历完,需要插入 j 个字符才能与 word2 匹配;同理,当 j = 0 时,需要删除 i 个字符才能与 word2 匹配。
5. 所求答案:最终的答案保存在 dp[n][m] 中,其中 n 和 m 分别是 word1 和 word2 的长度。
```go
func minDistance(word1 string, word2 string) int {
n,m:=len(word1),len(word2)
dp:=make([][]int,n+1)
for i:=0;i<=n;i++{
dp[i]=make([]int ,m+1)
}
for i:=0;i<=n;i++{
dp[i][0]=i
}
for j:=0;j<=m;j++{
dp[0][j]=j
}
for i:=0;i<n;i++{
for j:=0;j<m;j++{
if word1[i]==word2[j]{
dp[i+1][j+1]=dp[i][j]
}else{
dp[i+1][j+1]=min(dp[i][j+1],dp[i+1][j],dp[i][j])+1
}
}
}
return dp[n][m]
}
func min(x, y, z int) int {
if x < y && x < z {
return x
} else if y < x && y < z {
return y
}
return z
}
```