Back-propagation AlgorithmIf we have a neural network with o

If we have a neural network with only 1 hidden layer and 1 output layer, the structure is as follows:

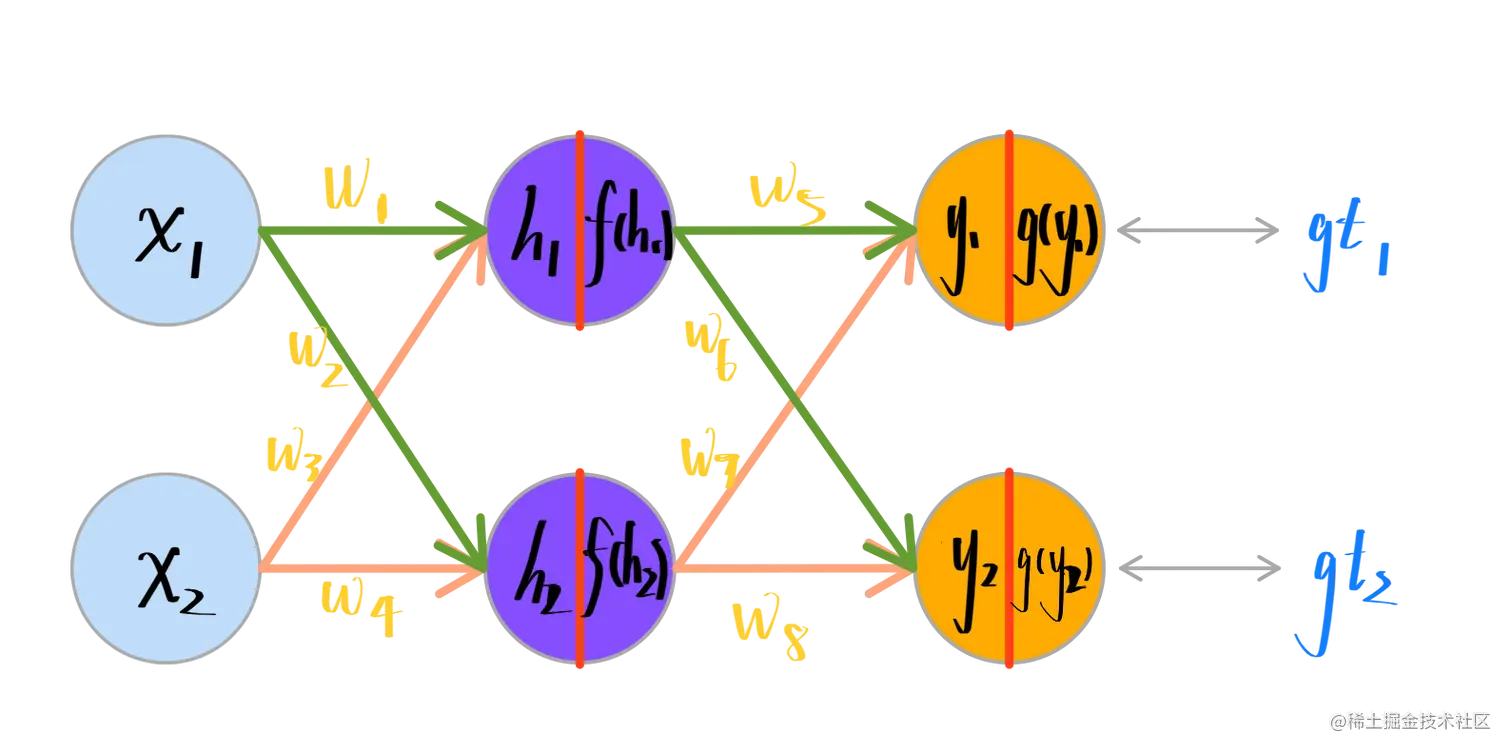Neural Network so the forward path of $g(y_1)$ is as equation below: output: $f\left(y_1\right)$

\begin{aligned} & y_1=w_5 f\left(h_1\right)+w_7 f\left(h_2\right) \\ & h_1=w_1 x_1+w_3 x_2 \end{aligned}

So the error of the $f(y_1)$ is denoted as: $Error(y_1)=\frac{(gt_1 - g(y_1))^2}{2}$ So the back-propagation for $w_5$ is as follows based on the chain rule:

\frac{\partial Error(y_1)}{\partial w_5}=\frac{\partial Error(y_1)}{\left.\partial f(y_{y_1}\right)} \times \frac{\partial f\left(y_1\right)}{\partial y_1} \times \frac{\partial y_1}{\partial w_5}

When we got the real value of $\frac{\partial Error}{\partial w_5}$ , we can update the weight $w_5$ :

w_5^{+}=w_5-\eta \frac{\partial Error(y_1)}{\partial w_5}

This is as same as $w_6$ :

w_6^{+}=w_6-\eta \frac{\partial Error(y_2)}{\partial w_6}

Furthermore, the back-propagation for $w_1$ is as follows:

\begin{aligned} \frac{\partial \text { Error }}{\partial w_1} & =\frac{\partial \operatorname{Error}\left(y_1\right)}{\partial w_1}+\frac{\partial \operatorname{Error}(y_2)}{\partial w_1} \\ & =\frac{\partial Error{\left(y_1\right)}}{\partial g\left(y_1\right)} \frac{\partial\left(y_1\right)}{\partial y_1} \frac{\partial y_1}{\partial f\left(h_1\right)} \frac{\partial f\left(h_1\right)}{\partial h_1}\frac{\partial h_1}{\partial w_1} \\ & + \frac{\partial Error{\left(y_2\right)}}{\partial g\left(y_2\right)} \frac{\partial\left(y_2\right)}{\partial y_2} \frac{\partial y_2}{\partial f\left(h_1\right)} \frac{\partial f\left(h_1\right)}{\partial h_1}\frac{\partial h_1}{\partial w_1} \end{aligned}

So we can update the $w_1$ by the gradient:

w_1^+=w_1-\eta \frac{\partial \text { Error }}{\partial w_1}