论文《Controllable Multi-Interest Framework for Recommendation》

阿里ComiRec

论文地址：dl.acm.org/doi/pdf/10.… git地址：github.com/THUDM/ComiR…

阿里的ComiRec是对多兴趣召回的一个阶段性总结。

多兴趣抽取模块总结了2种方法：一个是之前应用到MIND的Capsule Network，一个是Self-Attention 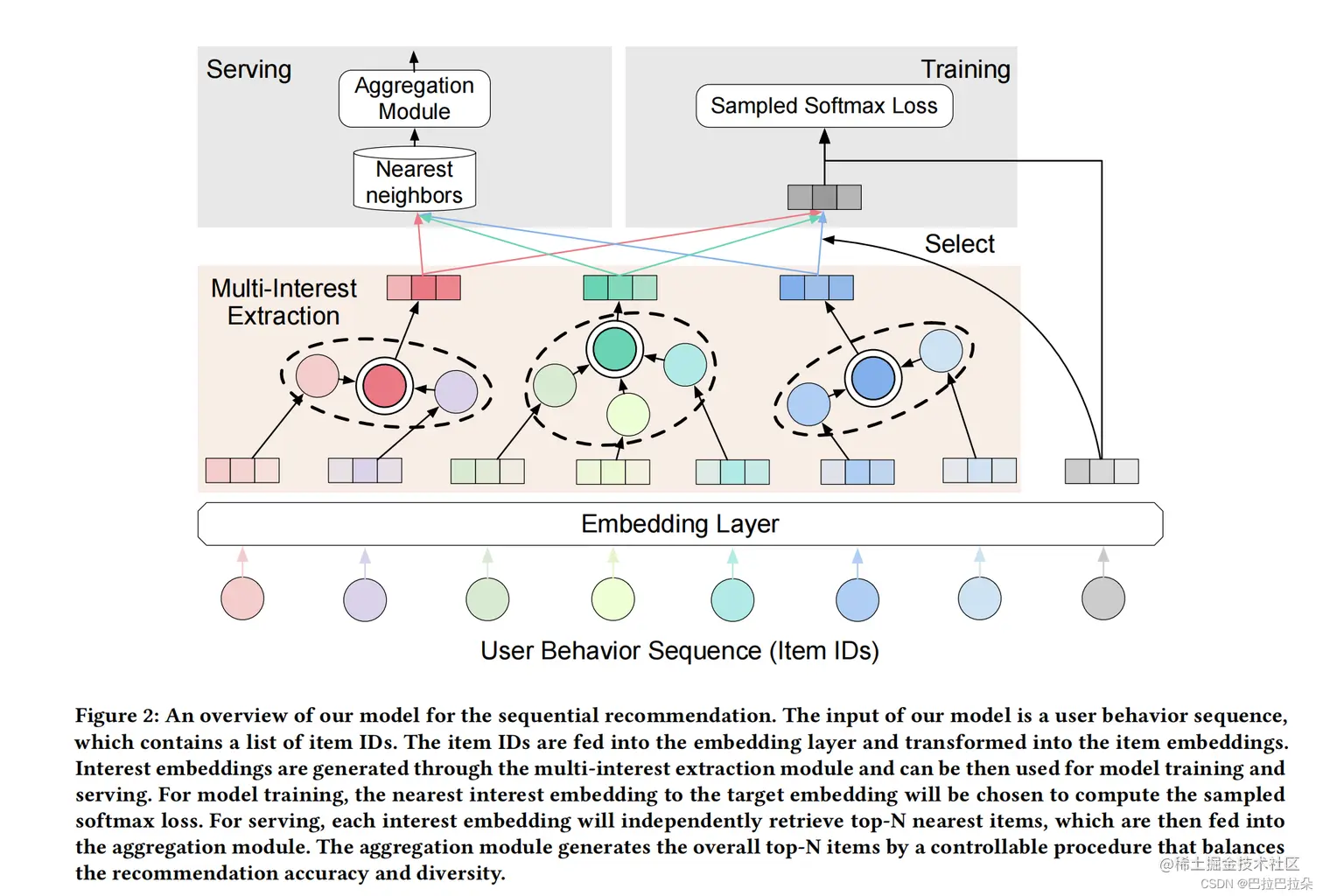对于Self-Attention方法，给定用户行为序列Embedding $\mathbf H \in R^{d \times n}$，$d$是兴趣向量维度，$n$是用户的序列长度（sequence-length），attention的权重向量计算如下

$\mathbf a$ = softmax($\mathbf w_2^T$tanh($\mathbf W_1 \mathbf H$)) $\in R^n$ $\mathbf W_1 \in R^{d_a \times d}$ , $\mathbf w_2 \in R^{d_a \times 1}$ 权重求出来后，应用到用户序列Embedding上面，就得到用户的Embedding $\mathbf v_u = \mathbf H \mathbf a \in R^{n}$ 为了表示多个用户兴趣，将$\mathbf w_2$的维度扩展$K$倍，变成矩阵$\mathbf W_2 \in R^{d_a \times K}$ 注意力权重向量变成了注意力权重矩阵 $\mathbf A$ = softmax$(\mathbf W_2tanh( \mathbf W_1 \mathbf H))$ $\in R^{n \times K}$ $\mathbf V_u = \mathbf H \mathbf A$ $\in R^{n \times d}$

模型训练

计算出用户的多个兴趣Embedding之后，根据目标item的Embedding $\mathbf e_i$,使用$argmax$操作来确定最终的用户Embedding $\mathbf v_u = \mathbf V_u[:,argmax(\mathbf V_u^T \mathbf e_i)]$ 损失函数 $loss = \sum_{u \in \mathbf U} \sum_{i \in \mathbf I_u} - \log P_{\theta} (i | u)$ $P_{\theta}(i|u) = \frac {exp(\mathbf v_u^T \mathbf e_i)} {\sum_{i \in I_u} exp(\mathbf v_u^T \mathbf e_i) }$

合并策略

每个兴趣Embedding都可以检索出topN个最相关的候选物料，如何合并$K$个兴趣Embedding的结果，一种简单的做法是对于同时出现在多个兴趣Embedding相似结果的物料，其最终打分可以用max/sum等策略来解决，max策略比较强调某一个兴趣的单一相似度，sum强调多个兴趣总的相似度。论文基于max策略结合类目多样性限制提出了一个新的合并策略。 首先max分数结果如下,$\mathbf v_u^{(k)}$是是第k个用户兴趣向量 $f(u,i) = \underset{x\in S} \max (\mathbf e_i^T \mathbf v_u^{(k)})$ 设$S$是$K$个兴趣Embedding检索到的候选集去重后的数量，$Q(u,S)$表示结合max策略和类目多样性的打分结果 $Q(u,S) = f(u,i) + \lambda \sum_{i \in S} \sum_{j \in S} g(i,j)$ 其中$g(i,j)=\delta(CATE(i) \neq CATE(j))$表示类目多样性，$\lambda=0$表示只要准确性，不要多样性，$\lambda=\infty$表示要推荐最多样化类目的候选给用户

评估指标

$\hat I_{u,N}$表示topN候选结果集合，$I_u$表示测试集用户$u$真实的交互物料集合 Recall 表示每个用户的平均准确率

Recall@N$=\frac {1} {\vert U \vert } \sum_{u \in U} \frac {\vert \hat I_{u,N} \bigcap I_u \vert } {\vert I_u \vert}$ Hit Rate表示topN推荐结果中至少包含一个测试集用户$u$真实交互物料的比例 HR@N=$\frac {1} {\vert U \vert } \sum_{u \in U} \delta(\vert \hat I_{u,N} \bigcap I_u \vert > 0)$ NDCG考虑了推荐结果的位置 NDCG@N=$\frac{1}{Z}$NCG@N=$\frac{1}{Z} \frac {1}{\vert U \vert }\sum_{u \in U} \sum_{k=1}^K \frac {\delta(\hat i_{u,k} \in I_u)} { \log_2(k+1)}$

兴趣提取模块究竟是capsule还是self-attention好要看实际业务场景，不同场景应用可能结果不同