分治法——一维空间最小点对问题

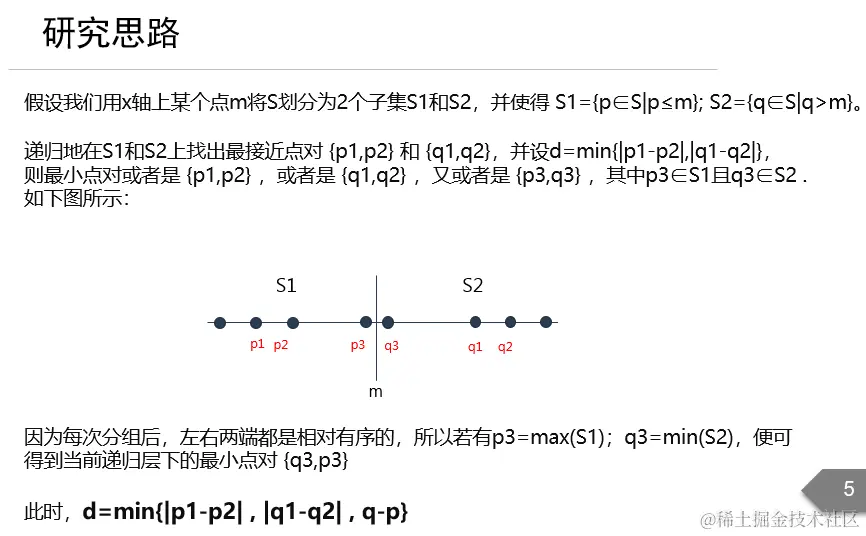
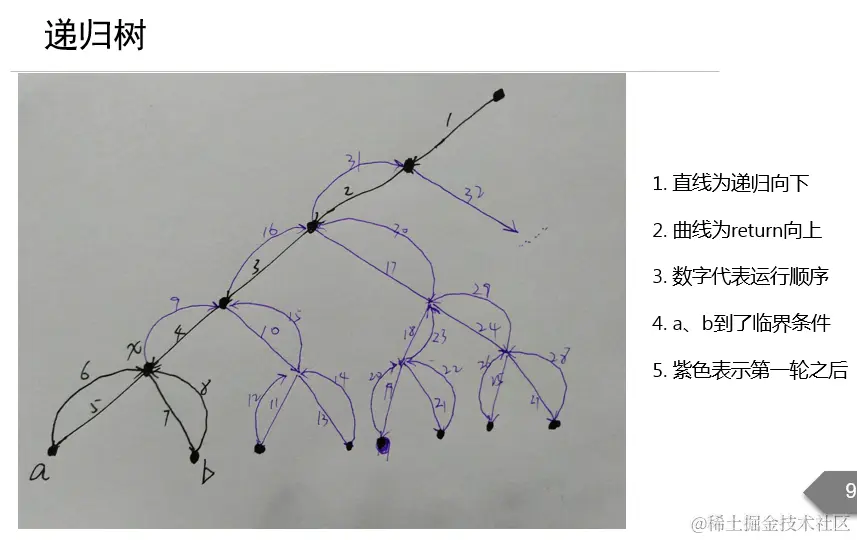
代码

#include <iostream>
#include <cstdio>
#include <ctime>
#include <cstdlib>
#include <algorithm>
#include <cmath>
using namespace std;

double p, q, mid;
double *a;
int N;

struct Point
{
    double d;      // 记录两个点之间的距离
    double d1, d2; // 记录两个点
};

int Partition(int low, int high)
{
    int i = low, j = high + 1;
    double x = a[low];
    while (1)
    {
        while (a[++i] < x && i < high)
            ;
        while (a[--j] > x)
            ;
        if (i >= j)
            break;
        swap(a[i], a[j]);
    }
    swap(a[low], a[j]);

    return j;
}

int GetMid(int l, int r)
{
    int mid = (l + r) / 2;
    while (1)
    {
        int pos = Partition(l, r);
        if (pos == mid)
            break;
        else if (pos > mid)
            r = pos - 1;
        else
            l = pos + 1;
    }
    return mid; // 中位数的下标
}

Point CPair(int low, int high)
{
    Point kua = {0x3f3f3f3f, 0, 0}; // 0x3f3f3f3f:无穷大   // 用来记录两个点分布在两边的情况
    if (low >= high)
        return kua; // 退出

    int m = GetMid(low, high); // m为中位数的下标

    // cout<<m<<endl;

    Point d1 = CPair(low, m);      // 左半边
    Point d2 = CPair(m + 1, high); // 右半边

    p = (*max_element(a + low, a + m + 1));      // 指定左区间求最大值
    q = (*min_element(a + m + 1, a + high + 1)); // 指定右区间求最小值

    //先为kua赋上值
    kua.d = q - p; // kua的距离为右边最小值和左边最小值的差
    kua.d1 = q;
    kua.d2 = p;

    return d1.d < d2.d ? (d1.d < q - p ? d1 : kua) : (d2.d < q - p ? d2 : kua); // 使用三目运算符嵌套。 来返回距离d值最小的那个结构体
}

int main()
{
    // srand((unsigned)time(NULL));   // 初始化随机种子
    // freopen("a.txt","r",stdin);   // 使用随机数的缺点就是一次次的生成，可能会出现重复值
    cin >> N;
    a = new double[N];
    cout << "读取到的一维点个数为：" << N << endl
         << "分别是:";
    for (int i = 0; i < N; i++)
    {
        // cin>>a[i];
        a[i] = (rand() % 1000 - 100) * 0.01;
        cout << a[i] << "  ";
    }
    cout << endl
         << endl
         << endl;

    Point res = CPair(0, N - 1);

    cout << "最近点对为：" << res.d1 << "  " << res.d2 << endl;
    cout << "其距离为： " << res.d << endl;
}

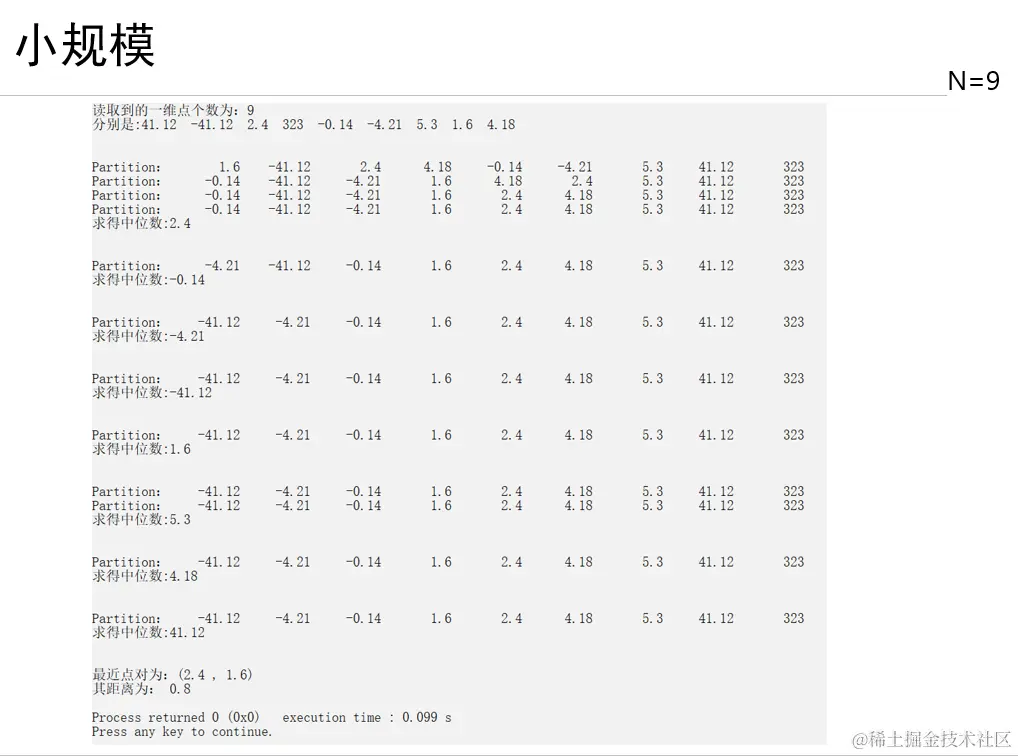
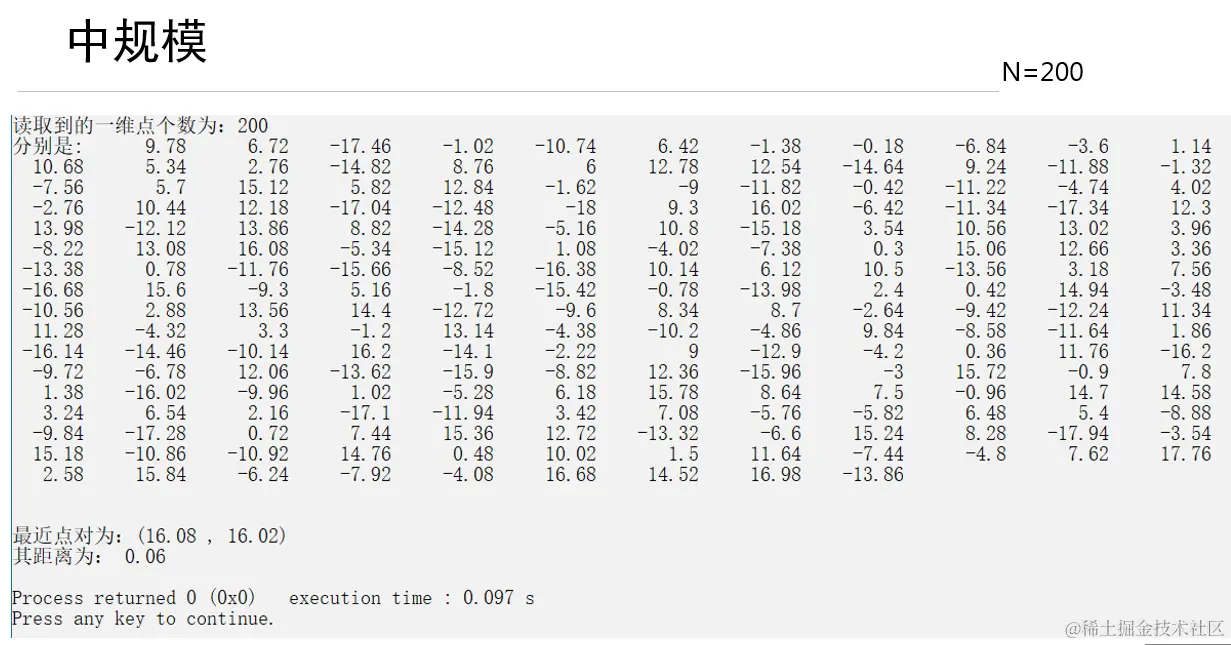
运行结果

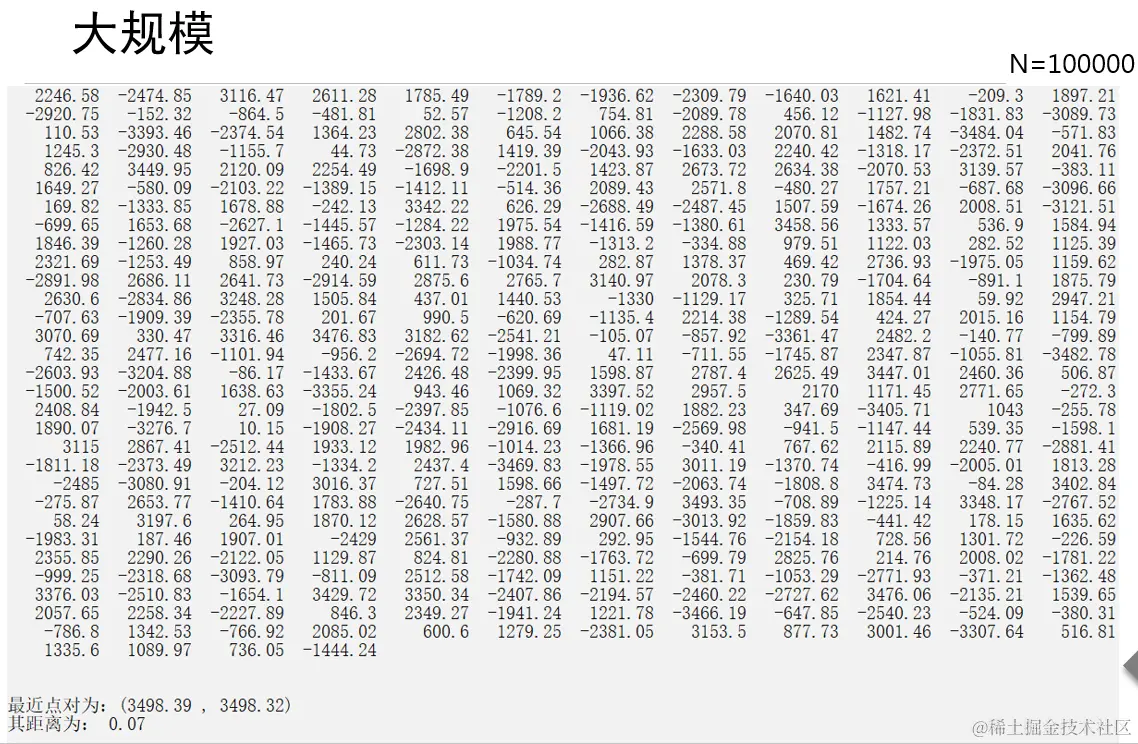
复杂度分析