本文从互联网搬运,只用于本人学习记录。
决策树之集成学习
集成学习优于单个学习器:
- 训练样本可能无法选择出最好的单个学习器,由于没法选择出最好的学习器,所以干脆结合起来一起用;
- 假设能找到最好的学习器,但由于算法运算的限制无法找到最优解,只能找到次优解,采用集成学习可以弥补算法的不足;
- 可能算法无法得到最优解,而集成学习能够得到近似解。比如说最优解是一条对角线,而单个决策树得到的结果只能是平行于坐标轴的,但是集成学习可以去拟合这条对角线。
偏差 & 方差:
偏差Bias:描述的是预测值和真实值之差。要想偏差表现的好,就需要复杂化模型,容易过拟合。
方差Variance:描述样本上训练出来的模型再测试集上的表现,要想方差表现的好,需要简化模型,容易欠拟合。
Bagging和Stacking中的基模型为强模型(偏差低、方差高),而Boosting中基模型为弱模型(偏差高,方差低)。
对于Bagging来说,整体模型的偏差与基模型近似,而随着模型的增加可以降低整体模型的方差,故其基模型需要为强模型;
对于Boosting来说,整体模型的方差与基模型近似等于,而整体模型的偏差由基模型累加而成,故基模型需要为弱模型。
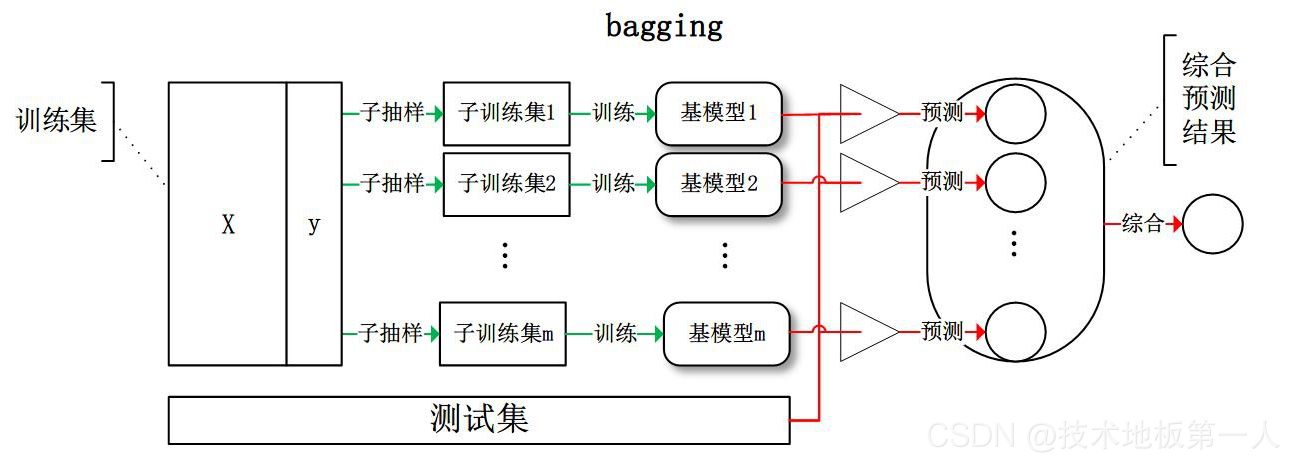
Bagging
每个基学习器都会对训练集进行有放回抽样得到咨询练级,如0.632自助采样法。
每个基学习器基于不同子训练集进行训练,并综合所有基学习器的预测值得到最终的预测结果。常用的综合方法是投票法,票数最多的类别为预测类别。
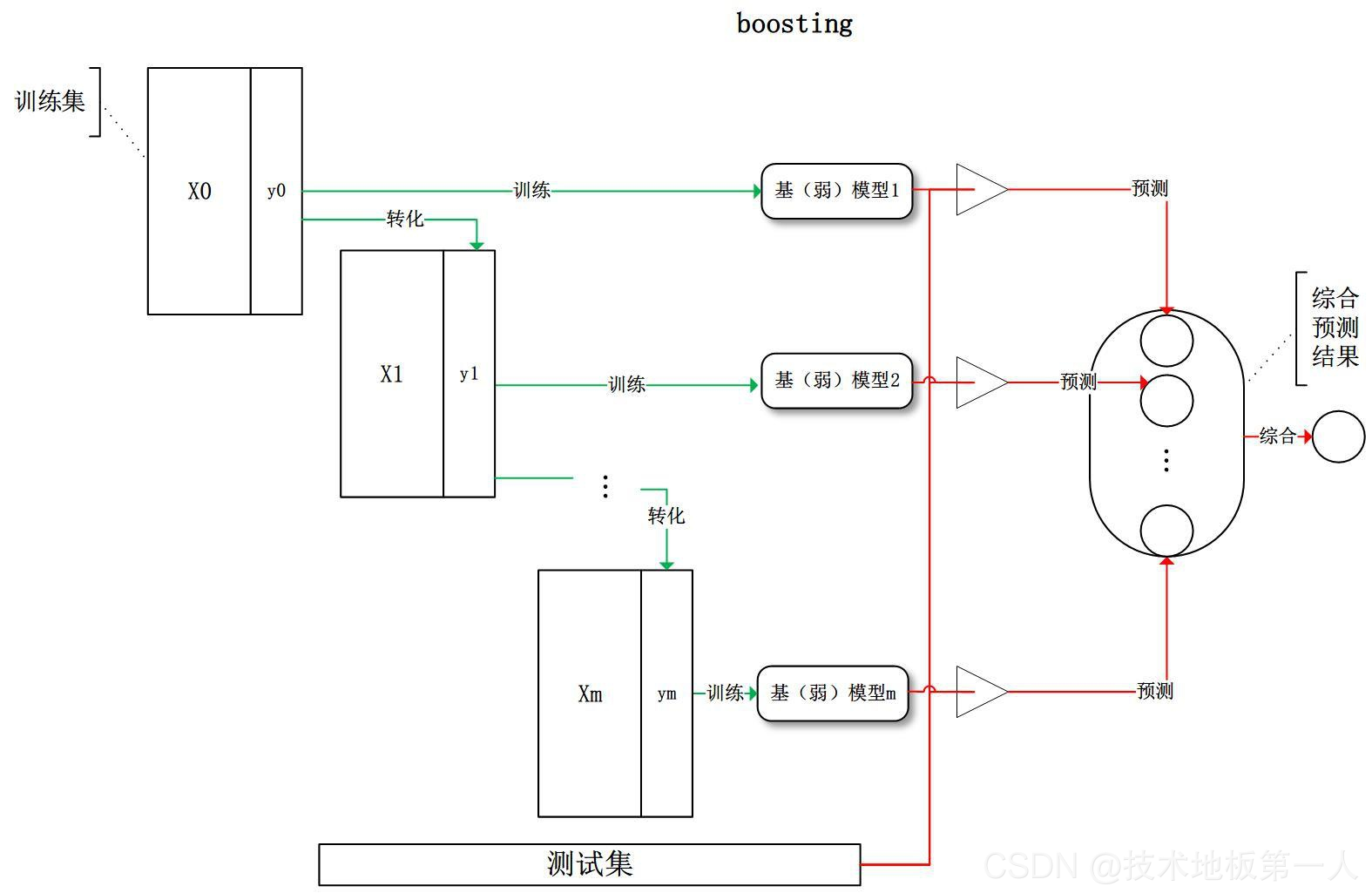
Boosting
Boosting 训练过程为阶梯状,基模型的训练是有顺序的,每个基模型都会在前一个基模型学习的基础上进行学习,最终综合所有基模型的预测值产生最终的预测结果,用的比较多的综合方式为加权法。
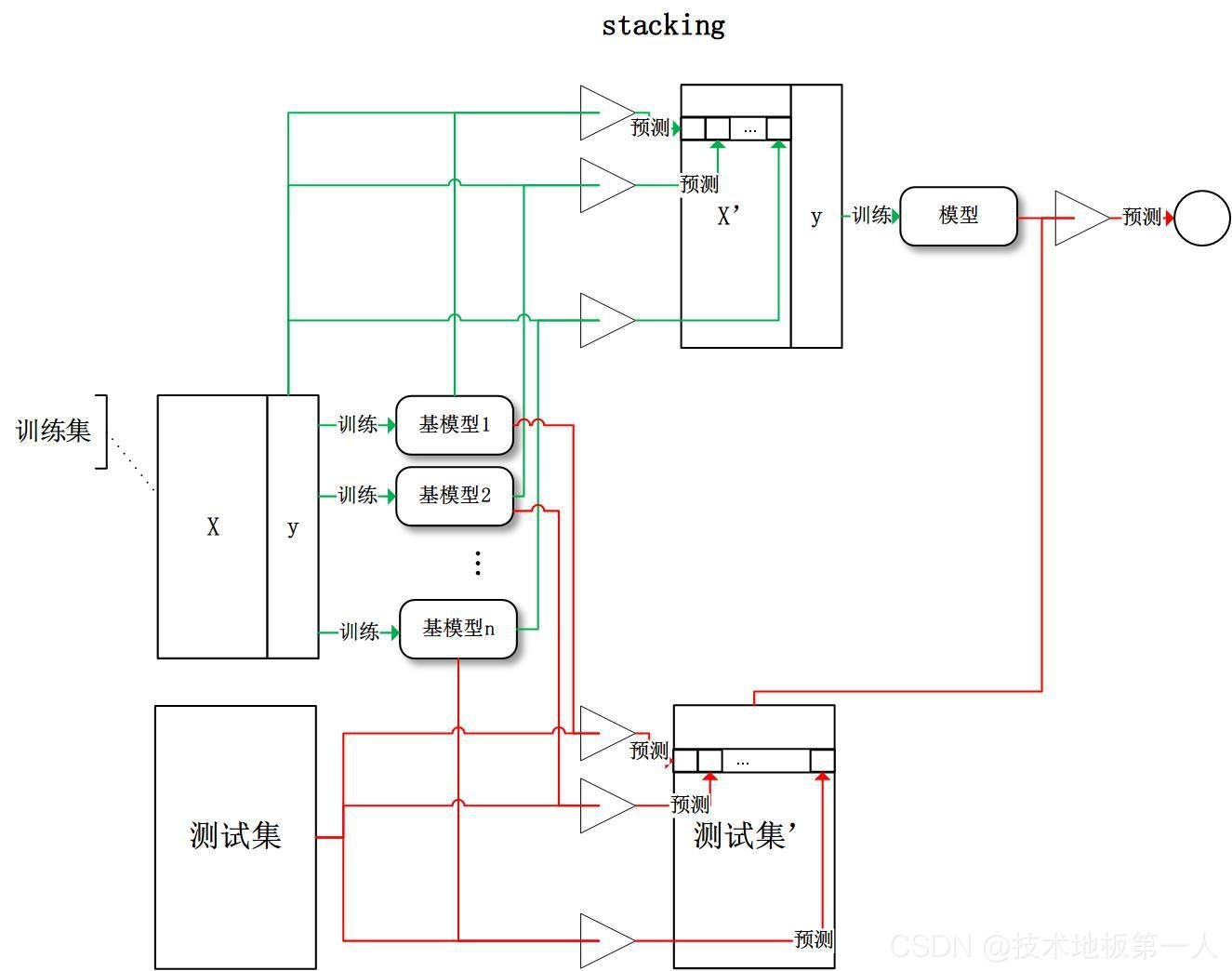
Stacking
Stacking 是先用全部数据训练好基模型,然后每个基模型都对每个训练样本进行的预测,其预测值将作为训练样本的特征值,最终会得到新的训练样本,然后基于新的训练样本进行训练得到模型,然后得到最终预测结果。
随机森林 Random Forest
用随机的方式建立一个森林。RF 算法由很多决策树组成,每一棵决策树之间没有关联。建立完森林后,当有新样本进入时,每棵决策树都会分别进行判断,然后基于投票法给出分类结果。
1. 思想
在以决策树为基学习器构建Bagging集成的基础上,进一步在决策树的训练过程中引入了随机特征选择,因此可以概括RF包括四个部分:
- 随机选择样本(放回抽样);
- 随机选择特征;
- 构建决策树;
- 随机森林投票(平均)。
随机选择样本和Bagging相同,采用的是Bootstrap自助采样法;随机选择特征是指在每个节点在分裂过程中都是随机选择特征的(区别与每棵树随机选择一批特征)。
这种随机性导致随机森林的偏差会有稍微的增加(相比于单棵不随机树),但是由于随机森林的**“平均”特性,会使得它的方差减小**,而且方差的减小补偿了偏差的增大,因此总体而言是更好的模型。
随机采样由于引入了两种采样方法保证了随机性,所以每棵树都是最大可能的进行生长就算不剪枝也不会出现过拟合。
2. 优缺点
优点:
- 在数据集上表现良好,相对于其他算法有较大的优势;
- 易于并行化,在大数据集上有很大的优势;
- 能够处理高维度数据,不用做特征选择。
缺点:
- 在某些噪声较大的分类和回归问题上会过拟合;
- 级别划分较多的属性会对随机森林产生更大的影响,在这种数据上产生的属性权值是不可信的。
3. 与GDBT对比

4. 调参
n_estimators:
随机森林中树的个数,默认是10棵。
n_jobs=-1:
并行job个数。这个在ensemble算法中非常重要,尤其是bagging(而非boosting,因为boosting的每次迭代之间有影响,所以很难进行并行化),因为可以并行从而提高性能。1:不并行;n:n个并行;-1:CPU有多少core,就启动多少job。
max_depth:
就是这个树的深度,决定了能够决策的条件树,默认就是分割到每个子结点仅省一个数据,这样就是最精确的,所以决策树的问题往往就是过拟合、范化能力差。
oob_score:
袋外估计(out-of-bag),这个外是针对于bagging这个袋子而言的,我们知道,bagging采取的随机抽样的方式去建立树模型,那么那些未被抽取到的样本集,也就是未参与建立树模型的数据集就是袋外数据集,我们就可以用这部分数据集去验证模型效果,默认值为False。
bootstrap:
是统计学中的一种重采样技术,可以简单理解成是有放回地抽样,默认是True,即采取有放回抽样这种策略,这不就是bagging的思想么。