【单智能体应用、分配算法、基于Q-learning】基于强化学习的电动汽车充电站收益最大化算法【单智能体应用、分配算法、

【单智能体应用、分配算法、基于Q-learning】基于强化学习的电动汽车充电站收益最大化算法

Reinforcement Learning Based Algorithm for the Maximization of EV Charging Station Revenue

基于Q-learning算法
单智能体的强化学习
大多参数是利用统计学，使用历史数据归纳得出的

具体实现

参数设置
- 设置为一个episode为一天，一个小时step一次
- $t_1=1,2,..,T$ 其中 $T=24$ 车辆以任何时间到达电站，但最早需要在下一小时开始时充电
- 电站有 $k$ 个充电车位，最多容纳 $M$ 辆车（ $M=k+等待充电车辆$ ）
- 用函数 $f(x)$ 表示车辆到达不同充电状态的支付费用（期望时间内获取的电量越多（快充）则越贵）， $x$ 为车辆充电状态 $SOC$ ； $x_1=SOC x_1$ 为初始态（在实验中根据历史信息手动配置）； $x_2$ 为需求状态（由用户提供）；则 $价格=f(x_2)-f(x_1)$ ，电站还会获取车辆预计离开时间（TTL）
- 电站在某个 $t$ 时刻获得自身电力供应 $r(t)$ ；此外，电站还可以以 $p(t)$ 价格购买额外的电量，价格是变化的；（在实验中 $r(t)$ 和 $p(t)$ 根据统计的历史数据直接给出确定值；）
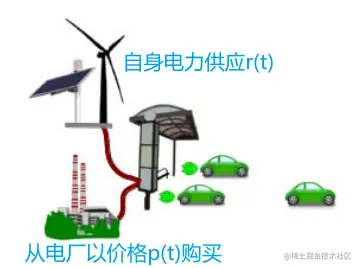
环境
- 观察/状态向量为
  
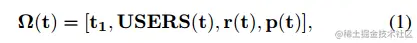
  其中， $t_1$ 表示一天中的小时， $USERS(t)=\{\{TTL(t),SOC(t),Types(t)\}_1,\{TTL(t),SOC(t),Types(t)\}_2,...,\{TTL(t),SOC(t),Types(t)\}_M\}$
  
  $TTL(t)$ 为0~ $ttl_{max}$ 之间的整数， $ttl_{max}$ 被设置为12； $SOC$ 被设置为0,10,20,...,90,100；假设每辆车的电池容量相同；在实验中， $Types$ 被设置为 $富裕用户rich，普通用户medium$ ；
- 车辆抵达服从泊松分布，时间间隔(a, b)内到达的数量，用N(b)-N(a)表示
  
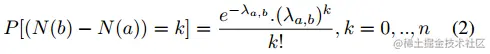
  因此，到达的数量为 $z(t)\sim P_o(λ_{t,t+1})$ ，t∈1,2,...,23， $λ_{t,t+1}$ 为均值，带入k即可计算每个时段到达k个车辆的概率
- 动作空间：（充电量）动作向量为 $u_i(t)=0,10,...,100-SOC_i(t)$
  
  SOC向量更新为 $SOC(t)=SOC(t)+u(t)$
  
  TTL减少1的变化： $TTL(t+1)=TTL(t)-\vec 1$ ，当TTL为0时将车辆移除
  
  在每个时间步数组按TTL排序，如果TTL一致，则按类型排序
- 奖励函数 $Φ$ ：
- 值函数：
  
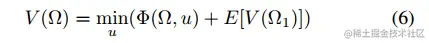
  使用Q-learning的近似值函数：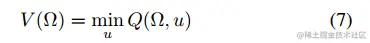
- 价格函数f(x)：
  
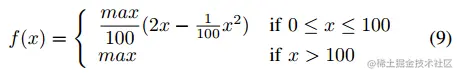
  max指的是一辆最初空着的汽车充满电的价格，根据实验， $max_{rich}$ =3.6 ， $max_{medium}$ =2.4