什么是线性回归

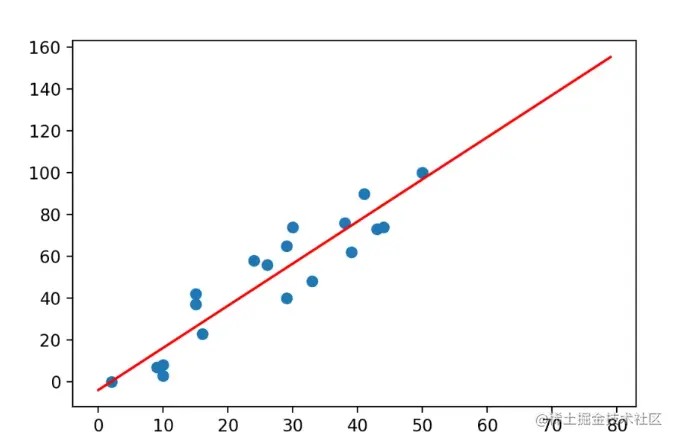
线性回归的基本假设是，变量之间的关系可以用一个或多个线性方程来近似表示。例如，如果我们只用一个自变量x来预测因变量y，例如：在这里插入图片描述

那么此时我们可以假设y和x之间有如下的线性方程：

$y=\beta_0+\beta_1x+\mu$

其中， $\beta_0$ 和 $\beta_1$ 是线性回归的参数，也叫做回归系数，它们表示了x和y之间的线性关系的强度和方向。 $\mu$ 是误差项，它表示了y的真实值和预测值之间的差异，通常假设它服从均值为0的正态分布。这样一来，假设，我们可以求解出这个方程的大致参数，那么我们就可以非常轻松地完成对后续数据的大体预测。那么这就是一个一般的一元线性回归。

同理，在一般情况下，我们按照对应关系来进行划分，我们还有多元线性回归，例如，我们的数据可能满足如下表格的信息。

x1	x2	y
1	2	6
2	3	7
3	4	10
4	5	11

我们接下来需要X到Y的关系进行线性的表述，以便于完成预测等任务。

线性回归的求解

这里，我们从一元线性回归出发。实际上，我们的根本目标其实是，我们希望找到一条线性直线，能够非常完美的去近似表示数据的分布。

于是我们假设这些数据满足，或者能够用下列公式进行表示： $y=\beta_0+\beta_1x+\mu$ 我们的重点就是方程当中的未知系数，对于我们来说，x,是已知的，当然误差也是未知的，但是当我进行近似求解的时候，误差项将可以被忽视。此时由于系数未知，不同的系数可以产生不同的直线，那么我们需要找到一个合适的系数，能够最大限度的去拟合。因此在这里我们可以定义，那就是，对于一条拟合的直线来说，我们认为，能够满足总体的预测值与实际值的误差最小的方程就是满足要求的方程。

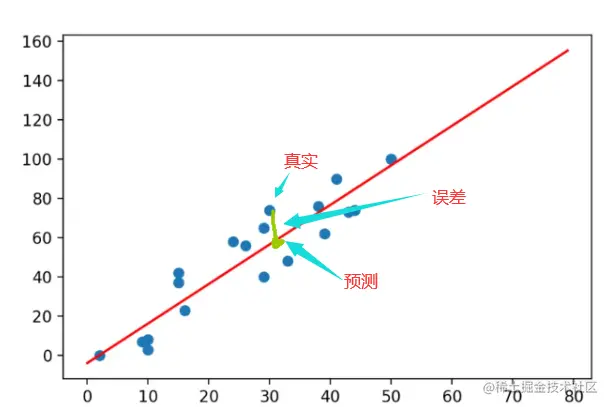
换一句话说如图所示：在这里插入图片描述

一元线性回归（最小二乘法）

此时，我们可以很容易的用数学语言去描述我们刚刚说的过程，那就是：

$Q=\sum_{i=1}^n(y_i-\hat{y}_i)^2=\sum_{i=1}^n(y_i-(\hat{\beta}_0+\hat{\beta}_1x_i))^2$

而，这个方法就叫做最小二乘法。

对于每一个观测值 $(x_i,y_i)$ ，我们计算它的残差（真实值和预测值之间的差值） $e_i=y_i-\hat{y}_i$ 此时我们也可以将这个看作损失函数。

这个损失函数反映了预测值和真实值之间的总偏差，我们希望找到一组回归系数 $\hat{\beta}_0$ 和 $\hat{\beta}_1$ ，使得这个损失函数达到最小值。这相当于在二维空间中找到一条直线，使得所有数据点到这条直线的距离之和最小。

为了求解最小二乘法，我们利用微积分中求极值的方法，对损失函数分别对 $\hat{\beta}_0$ 和 $\hat{\beta}_1$ 求偏导数，并令其等于0：

$\frac{\partial Q}{\partial \hat{\beta}_0}=-2\sum_{i=1}^n(y_i-\hat{\beta}_0-\hat{\beta}_1x_i)=0$

$\frac{\partial Q}{\partial \hat{\beta}_1}=-2\sum_{i=1}^n(y_i-\hat{\beta}_0-\hat{\beta}_1x_i)x_i=0$

解这个方程组：

$\hat{\beta}_1=\frac{n\sum_{i=1}^nx_iy_i-\sum_{i=1}^nx_i\sum_{i=1}^ny_i}{n\sum_{i=1}^nx_i^2-(\sum_{i=1}^nx_i)^2}$

$\hat{\beta}_0=\frac{1}{n}\sum_{i=1}^ny_i-\hat{\beta}_1\frac{1}{n}\sum_{i=1}^nx_i$

最后我们完成求解：

$y=\hat{\beta}_0+\hat{\beta}_1x$

多元线性回归

对于多元线性回归方程：

$y=\beta_0+\beta_1x_1+\beta_2x_2+...+\beta_kx_k+\mu$

我们也可以使用类似的方法求解。同样的，我们将公式展开带入：

$Q=\sum_{i=1}^n(y_i-\hat{y}_i)^2=\sum_{i=1}^n(y_i-(\hat{\beta}_0+\hat{\beta}_1x_{i1}+\hat{\beta}_2x_{i2}+...+\hat{\beta}_kx_{ik}))^2$

同样的，我们采用我们利用微积分中求极值的方法：

$\frac{\partial Q}{\partial \hat{\beta}_0}=-2\sum_{i=1}^n(y_i-\hat{\beta}_0-\hat{\beta}_1x_{i1}-\hat{\beta}_2x_{i2}-...-\hat{\beta}_kx_{ik})=0$

$\frac{\partial Q}{\partial \hat{\beta}_1}=-2\sum_{i=1}^n(y_i-\hat{\beta}_0-\hat{\beta}_1x_{i1}-\hat{\beta}_2x_{i2}-...-\hat{\beta}_kx_{ik})x_{i1}=0$

$\frac{\partial Q}{\partial \hat{\beta}_2}=-2\sum_{i=1}^n(y_i-\hat{\beta}_0-\hat{\beta}_1x_{i1}-\hat{\beta}_2x_{i2}-...-\hat{\beta}_kx_{ik})x_{i2}=0$

$...$

$\frac{\partial Q}{\partial \hat{\beta}_k}=-2\sum_{i=1}^n(y_i-\hat{\beta}_0-\hat{\beta}_1x_{i1}-\hat{\beta}_2x_{i2}-...-\hat{\beta}_kx_{ik})x_{ik}=0$

这个时候，我们转化为矩阵形式（这里省略了...laxtex格式有点问题）

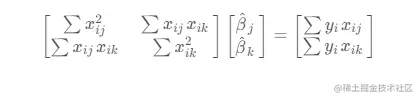
其中， $j,k=0,1,...,n$ 。

为了简化计算，我们可以用矩阵形式来表示多元线性回归方程和最小二乘法。令 $x_ {i0}=1$ ，则多元线性回归方程可以写成：（注：还有一个截距项μ，为了简化和保持统一，μ 我们可以看作是 1*βi）

$y=\mathbf{X}\boldsymbol {\beta}+\boldsymbol {\mu}$

其中，

\mathbf{X}= \begin{bmatrix} 1 & x_{11} & x_{12} & \dots & x_{1k} \\ 1 & x_{21} & x_{22} & \dots & x_{2k} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 1 & x_{n1} & x_{n2} & \dots & x_{nk} \end{bmatrix} , \mathbf{y}= \begin{bmatrix} y_1 \\ y_2 \\ \vdots \\ y_n \end{bmatrix} , \boldsymbol {\beta }= \begin{bmatrix} \beta _0 \\ \beta _1 \\ \vdots \\ \beta _k \end{bmatrix} , \boldsymbol {\mu }= \begin{bmatrix} \mu _1 \\ \mu _2 \\ \vdots \\ \mu _n \end{bmatrix}

损失函数改写写成：

$Q=(y-\mathbf{X}\boldsymbol {\beta })^\top (y-\mathbf{X}\boldsymbol {\beta })=\boldsymbol {\mu }^\top \boldsymbol {\mu }=\sum _ {i=1}^n (y_i-\mathbf{x}_{i}\boldsymbol {\beta })^ {2}$

其中， $\mathbf{x}_{i}$ 表示 $\mathbf{X}$ 的第 $i$ 行。

对损失函数求导，并令其等于零向量，得到：

$-2(\mathbf{X}\boldsymbol {\mu })^\top =-2(\mathbf{X}(y-\mathbf{X}\boldsymbol {\beta }))^\top =-2(\mathbf{X}\mathbf{y}-\mathbf{X}\mathbf{X}\boldsymbol {\beta })^\top =-2(\mathbf{y}^\top -(\mathbf{x}_{j}\boldsymbol {\mu })^\top )=0$

整理得到：

$(\mathbf{x}_{j}\boldsymbol {\mu })^\top =(\mathbf{x}_{j}(y-\mathbf{x}_{j}\boldsymbol {\beta }))^\top =(\mathbf{x}_{j}\mathbf{y}-\mathbf{x}_{j}\mathbf{x}_{j}\boldsymbol {\beta })^\top =(\mathbf{x}_{j}\mathbf{y})^\top -(\mathbf{x}_{j}\mathbf{x}_{j})^\top (\boldsymbol {\mu })^\top =(\mathbf{x}_{j}\mathbf{x}_{j})^\top (\boldsymbol {\mu })^\top$

从而得到正规方程组：

$(\mathbf{x}_{j}\mathbf{x}_{j})^\top (\boldsymbol {\mu })^\top =(\mathbf{x}_{j}\mathbf{y})^\top$

最后，我们整理一下，方程写成：

$\mathbf{X}^\top \mathbf{X} \boldsymbol{\beta} = \mathbf{X}^\top \mathbf{y}$

其中， $\mathbf{X}$ 是自变量矩阵， $\mathbf{y}$ 是因变量向量， $\boldsymbol{\beta}$ 是待求的参数向量。 之后我们假设矩阵是可逆的，那么左乘 $(\mathbf{X}^\top \mathbf{X})^{-1}$ ，得到：

$\boldsymbol{\beta} = (\mathbf{X}^\top \mathbf{X})^{-1}\mathbf{X}^\top \mathbf{y}$

完成求解。

衍生求解

此时，一个最基本的线性回归问题就被我们求解出来了。那么这个时候我们再回到我们刚刚一开始说的，其实不难发现，我们所有的一切，几乎都是围绕着： $Q=\sum_{i=1}^n(y_i-\hat{y}_i)^2=\sum_{i=1}^n(y_i-(\hat{\beta}_0+\hat{\beta}_1x_i))^2$

进行展开，通过它，我们可以求解出未知的系数。

那么问题来了，求解这个公式，我们有没有其他的方案？例如我们刚刚推到出我们使用正规方程来求解出我们的参数，但是这个过程当中存在求逆矩阵的过程，当参数量较大，特征多的情况下，这个逆矩阵显然很难求解，同时如果矩阵不是方阵，此时我们还只能求解伪逆，例如通过SVD等方案得到方阵进行运算（暴力理解）。那么这样一来，求解的系数似乎也不是那么准确。

此时，我们不得不面对残酷的现实，那就是理论求解，和实际上的工程实现当中存在一个新的误差，因为这个误差无论如何都难以避免，哪怕在不存在刚刚提到的问题，在计算机求解的过程当中也存在精度问题让结果不是100%准确。

梯度下降

因此，我们还可以使用其他的方案，我的目的是正对Q进行求解，我们系数当作未知数，对Q的请求当作最小化问题，当然实际上它就是最小化问题。

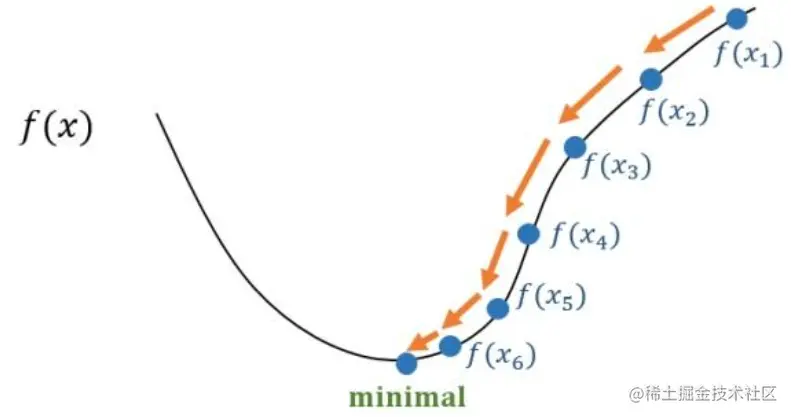
那么什么是梯度下降？用下面一张图其实非常好理解在这里插入图片描述

我们这里同样以一元线性回归为例子，当然多元的依然是一样的，前面的证明都是一样的。

通过上面这两个公式，我们可以求解出对应的偏导数： $\frac{\partial Q}{\partial \hat{\beta}_0}=-2\sum_{i=1}^n(y_i-\hat{\beta}_0-\hat{\beta}_1x_i)$

$\frac{\partial Q}{\partial \hat{\beta}_1}=-2\sum_{i=1}^n(y_i-\hat{\beta}_0-\hat{\beta}_1x_i)x_i$

一开始，我们可以先随机初始化，对应的系数 $\hat{\beta}_0$ , $\hat{\beta}_1$ 。此时我们最小化问题，显然只要让 $\hat{\beta}_0$ , $\hat{\beta}_1$ 往梯度相反的方向移动就好了，γ在这里表示学习率。

$\hat{\beta}_0 = \hat{\beta}_0 - γ\frac{\partial Q}{\partial \hat{\beta}_0}$

$\hat{\beta}_1 = \hat{\beta}_1 - γ\frac{\partial Q}{\partial \hat{\beta}_1}$

下面是一段代码示例：（这里偷了个懒，使用pytorch实现了自动求导功能）

import torch
import numpy as np
from matplotlib import pyplot as plt
#1,准备数据y=3X+0.8,准备参数
x = torch.rand([500,1])
# 这个是我们需要拟合的目标函数
y=3*x+0.8
w=torch.rand([1,1],requires_grad=True)
b=torch.tensor(0,requires_grad=True,dtype=torch.float32)

leanning = 0.01

for i in range(100):
    y_predict = torch.matmul(x,w)+b
    loss = (y - y_predict).pow(2).mean()
    if(w.grad is not None):
        w.grad.data.zero_()
    if(b.grad is not None):
        b.grad.data.zero_()
        
    loss.backward()
    w.data = w.data - leanning*w.grad
    b.data = b.data - leanning*b.grad
    # 在net当中会自动更新，咱们这个是最古老的版本
    if((1+i)%100==0):
        print("w,b,loss",w.item(),b.item(),loss.item())        
fig, ax = plt.subplots() # 创建图实例
ax.plot(x.numpy().reshape(-1),y.numpy().reshape(-1),label='y_true')
y_predict = torch.matmul(x,w)+b
ax.plot(x.numpy().reshape(-1),y_predict.detach().numpy().reshape(-1),label='y_pred')

运行结果如下：在这里插入图片描述当然这里还要值得一提的是，对应梯度的更新，也是有不同的策略的，这里就不展开说明了。

智能搜索算法求解（PSO）

那么同样的，显然我们还可以使用智能搜索算法来进行求解。例如，在这里，我们可以简单地使用PSO算法来进行求解。如果你熟悉，PSO算法的话，当然不熟悉也没关系，这只是一个拓展。我们可以很容易的进行如下操作，使得可以使用PSO算法进行求解。这段代码使用了PSO算法来求解线性回归的最优参数，具体步骤如下：

定义目标函数J(theta, X_b, y)，其中theta为待求解的参数向量，X_b为增广矩阵，y为样本标签。

构造100个样本数据，其中X为100x1大小的矩阵，y为100x1大小的矩阵。

将X矩阵的第一列加上一列1，得到增广矩阵X_b。

定义参数上下界lb和ub。

使用PSO算法求解最优参数theta_best和目标函数的最小值fopt，其中args=(X_b, y)表示传入X_b和y作为参数。

对应的代码如下：


import numpy as np
import matplotlib.pyplot as plt
from pyswarm import pso

# 定义目标函数
def J(theta, X_b, y):
    m = len(y)
    return 1/(2*m) * np.sum((X_b.dot(theta)-y)**2)

# 构造样本数据
X = 2 * np.random.rand(100, 1)
Y=3*X+0.8

# 把X矩阵的第一列加上一列1，得到增广矩阵X_b
X_b = np.c_[np.ones((100, 1)), X]

# 定义参数上下界
lb = np.array([-5, -5])
ub = np.array([5, 5])

# 使用PSO算法求解最优参数
theta_best, fopt = pso(J, lb, ub, args=(X_b, Y))

# 打印最优参数 theta_best
print(theta_best)
Y_P = theta_best[0]*X + theta_best[1]
# 绘制拟合直线和散点图
plt.plot(X, Y, "b.",label="real")
plt.plot(X, Y_P, "r-",label="preditct")
plt.legend()
plt.show()

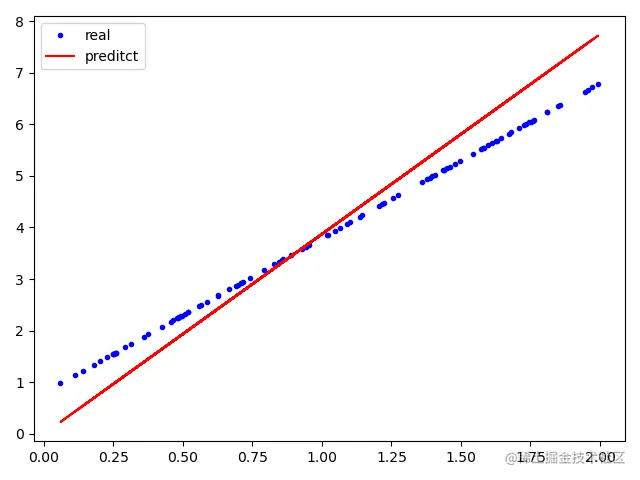
运行结果如下：在这里插入图片描述

简要分析

用PSO、正规方程和梯度下降这三种方法虽然都可以求解线性回归问题，它们但是他们都各有优缺点。

正规方程

正规方程是一种解析解法，可以直接求得最优的回归系数。在数据量不大的情况下，正规方程的计算速度较快，而且对于线性可分的数据集，其解析解是唯一存在的，因此具有较好的鲁棒性。但是，对于大规模数据集，在计算矩阵的逆和矩阵乘法时，时间和空间复杂度都较高，计算效率低下。此外，如果自变量之间存在相关性或者特征维度很高，计算矩阵逆的过程中可能会出现数值不稳定的问题。

梯度下降

梯度下降是一种迭代算法，每次根据目标函数的梯度方向调整参数，使得目标函数值不断逼近最小值，直到收敛为止。相比于正规方程，梯度下降算法不需要显式求解矩阵逆，因此可以处理更大规模的数据集，并且可以自动适应参数空间的曲面形状，可以处理非凸函数等复杂情况。但是，梯度下降算法需要调整学习率等超参数，并且容易陷入局部最优解，收敛速度也不一定最优。

PSO

相比于前两种方法，PSO是一种启发式、全局搜索的优化算法，可以用于求解更为复杂的非线性回归问题，并且具有较好的鲁棒性和泛化能力。同时，相较于梯度下降算法等其他迭代算法，PSO算法的并行化实现更为简单，在大规模数据的场景中具有一定的优势。但是，PSO算法利用局部搜索和全局搜索来寻找最优解，因此其计算效率较低，同时也无法保证一定能找到全局最优解。

线性回归与简单神经网络

联系

线性回归与简单神经网络，在很大程度上非常相似，实际上，当然我们采用梯度下降算法来求解线性回归方程时，其就相当于一个简单的不带激活函数的神经网络。

它们都是用来进行回归分析的方法，它们的主要区别在于模型的复杂度和灵活性。

线性回归是一种基本的、简单的模型，它假设自变量和因变量之间存在一个线性关系，并通过最小二乘法来求解最优的回归系数。线性回归的模型形式为：

$y = \theta_0 + \theta_1 x_1 + \theta_2 x_2 + \cdots + \theta_n x_n + \epsilon$

其中 $y$ 是因变量， $x_i$ 是第 $i$ 个自变量， $\theta_i$ 是回归系数， $\epsilon$ 是随机误差。

简单神经网络（Single-Layer Feedforward Neural Network，SLFN）是一种比线性回归更加灵活的模型，可以处理输入输出之间的非线性关系。它由多个神经元组成，每个神经元包括一个偏置项和多个输入权重，经过激活函数的处理之后输出一个值。若仅含有一个隐层的 SLFN 可以表示出任意复杂度的连续函数。它的模型形式为：

\begin{aligned} z_i &= \varphi(w_{i,0} + w_{i,1} x_1 + w_{i,2} x_2 + \cdots + w_{i,n} x_n) \\ y &= \sum\limits_{i=1}^m v_i z_i + \epsilon \end{aligned}

其中 $z_i$ 是第 $i$ 个隐层神经元的输出， $\varphi(\cdot)$ 是激活函数， $w_{i,j}$ 是输入到第 $i$ 个神经元的第 $j$ 个权重， $v_i$ 是第 $i$ 个隐层神经元到输出层的权重，其它符号含义同线性回归。

相比于线性回归，简单神经网络具有更多的参数和更高的模型复杂度，因此需要更多的样本数据进行训练和更长的训练时间。当然，简单神经网络也比线性回归更容易出现过拟合等问题。

关于对神经网络的求解，对于单层神经网络模型我们参考采用梯度下降算法来求解线性回归的方式类似。当然对于多层的线性神经网络模型来说。这个过程其实也是类似的。在这里我们可以和线性回归进行简单的对比融合。

类比推导

在线性回归过程当作，我们一直将我们需要求解的方程Q当作损失函数，之后采用对应的方法去求解，那个时候，我们将其叫做损失函数。那么在这里同样的，我们对这个公式进一步简化。

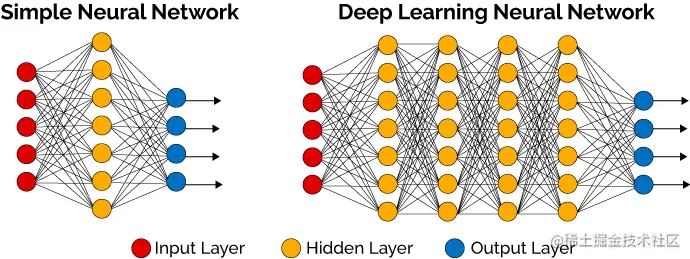
这是一个简单的神经网络模型，图像化是这样的：在这里插入图片描述

假设这是个具有 $L$ 层的前馈神经网络，其中第 $l$ 层的权重矩阵为 $W^{[l]}$ ，偏置向量为 $b^{[l]}$ ，激活函数为 $a^{[l]}(\cdot)$ 。输入样本为 $\boldsymbol{x}$ ，输出样本为 $\boldsymbol{y}$ ，则该神经网络的损失函数可以表示为：

\mathcal{L}(\boldsymbol{y}, \hat{\boldsymbol{y}}) = \frac{1}{2} ||\boldsymbol{y}-\hat{\boldsymbol{y}}||^2

其中， $\hat{\boldsymbol{y}}$ 表示神经网络对输入样本 $\boldsymbol{x}$ 的预测值。

反向传播

此时我们需要求出每一层的权重矩阵和偏置向量对损失函数的梯度(这个过程其实相当于在前面的使用梯度下降求解未知系数的过程)，以便用梯度下降算法来优化权重和偏置。而这个求解过程，我们叫做反向传播的过程。

对于输出层，我们可以直接计算其权重矩阵和偏置向量对损失函数的梯度。根据链式法则，输出层权重矩阵的梯度可以表示为：

\frac{\partial\mathcal{L}}{\partial W^{[L]}} = \frac{\partial\mathcal{L}}{\partial \hat{\boldsymbol{y}}} \frac{\partial\hat{\boldsymbol{y}}}{\partial (W^{[L]}\boldsymbol{a}^{[L-1]}+b^{[L]})} \frac{\partial(W^{[L]}\boldsymbol{a}^{[L-1]}+b^{[L]})}{\partial W^{[L]}}

其中， $\boldsymbol{a}^{[L-1]}$ 表示第 $L-1$ 层的激活值。通过链式法则，可以将上述公式转化为：

\begin{aligned} \frac{\partial\mathcal{L}}{\partial W^{[L]}} &= (\hat{\boldsymbol{y}} - \boldsymbol{y}) a^{[L-1]}(W^{[L]}\boldsymbol{a}^{[L-1]}+b^{[L]})' \\ &= (\hat{\boldsymbol{y}} - \boldsymbol{y}) a^{[L-1]}(\boldsymbol{z}^{[L]})\\ \end{aligned}

其中， $\boldsymbol{z}^{[L]} = W^{[L]}\boldsymbol{a}^{[L-1]}+b^{[L]}$ 表示第 $L$ 层的加权和， $'$ 表示对其求导。

同样地，输出层偏置向量的梯度可以表示为：

\frac{\partial\mathcal{L}}{\partial b^{[L]}} = \frac{\partial\mathcal{L}}{\partial \hat{\boldsymbol{y}}} \frac{\partial\hat{\boldsymbol{y}}}{\partial (W^{[L]}\boldsymbol{a}^{[L-1]}+b^{[L]})} \frac{\partial(W^{[L]}\boldsymbol{a}^{[L-1]}+b^{[L]})}{\partial b^{[L]}} = (\hat{\boldsymbol{y}} - \boldsymbol{y})

接下来，我们需要通过反向传播算法递归计算出每一层的权重矩阵和偏置向量对损失函数的梯度。以第 $l$ 层的权重矩阵为例，第 $l$ 层的梯度可以表示为：

\begin{aligned} \frac{\partial\mathcal{L}}{\partial W^{[l]}} &= \frac{\partial\mathcal{L}}{\partial\boldsymbol{z}^{[l]}} \frac{\partial\boldsymbol{z}^{[l]}}{\partial W^{[l]}} \\ &= \frac{\partial\mathcal{L}}{\partial\boldsymbol{a}^{[l]}} \frac{\partial\boldsymbol{a}^{[l]}}{\partial\boldsymbol{z}^{[l]}} \frac{\partial\boldsymbol{z}^{[l]}}{\partial W^{[l]}} \\ &= \frac{\partial\mathcal{L}}{\partial\boldsymbol{a}^{[l]}} g^{[l]\prime}(\boldsymbol{z}^{[l]}) (\boldsymbol{a}^{[l-1]})^T \end{aligned}

其中， $g^{[l]}(\cdot)$ 表示第 $l$ 层的激活函数， $g^{[l]\prime}(\cdot)$ 表示其导数。

对于第 $l$ 层的偏置向量，其梯度为：

\frac{\partial\mathcal{L}}{\partial b^{[l]}} = \frac{\partial\mathcal{L}}{\partial\boldsymbol{z}^{[l]}} \frac{\partial\boldsymbol{z}^{[l]}}{\partial b^{[l]}} = \frac{\partial\mathcal{L}}{\partial\boldsymbol{a}^{[l]}} g^{[l]\prime}(\boldsymbol{z}^{[l]})

通过递归地计算每一层的梯度，我们可以得到整个神经网络的权重矩阵和偏置向量对损失函数的梯度，从而利用梯度下降算法来更新网络参数，以最小化或最大化损失函数。

之后，和先前梯度下降求解线性回归一样： $\hat{\beta}_0 = \hat{\beta}_0 - γ\frac{\partial Q}{\partial \hat{\beta}_0}$