所谓摄像机标定,就是通过算法计算出摄像机的内外参
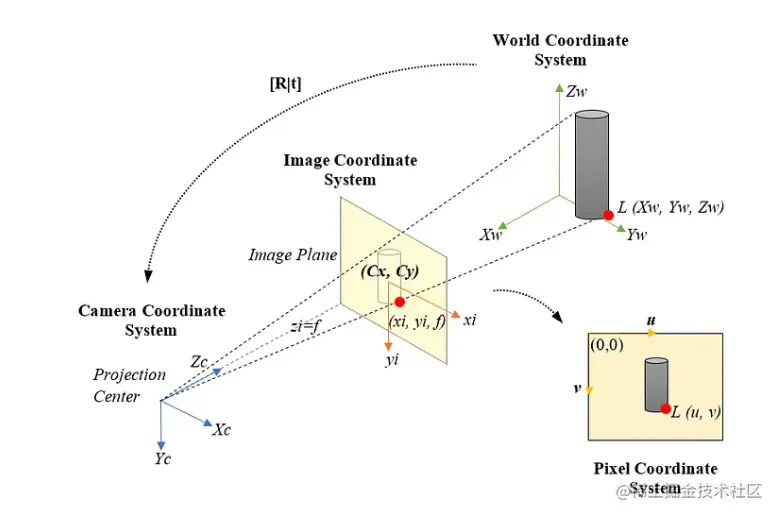
如果大家都以摄像机坐标系作为参考坐标系,那么当存在多个摄像机时,或者我们摄像机是运动的情况,就很难拿到统一标准。我们需要将摄像机坐标系描述 3 维物体的空间信息是否方便。所谓外参就是将物体从世界坐标系转摄像机坐标系,然后再由内参将摄像机坐标系的点转换为 2 成像平面的点。
P=[R0T1]Pw
- 这里下标 w 表示世界坐标系
- 其实这里之所以用到齐次坐标,是因为平移(T)并不是一个线性变换,无法用 3×3 的矩阵来对向量 (x,y,z) 进行线性变换得到
P′=K[I0]P=K[I0]Pw=K[RT]Pw=MPw
- 之所以叫作为外参是因为这个参数和摄像机姿态有关,而和摄像机自身无关,所以叫做外参
- 这里 K 是一个 3×3 矩阵
- I 是一个 3×3 单位阵,也就是对象线为 1 的矩阵
- 0 是一个 3×1 的列向量
- P 和 Pw 都是一个 4×1 的列向量
- M 是一个 3×4 的投影矩阵,也就是将世界坐标系下的点投影到像素平面上 P′ 的点
畸变
- 径向畸变,径向畸变来自于透镜形状,分为桶形畸变、枕形畸变
- 切向畸变,切向畸变来自整个摄像机的组装过程,切向畸变是透镜与成像平面不完全平行的制造缺陷造成的
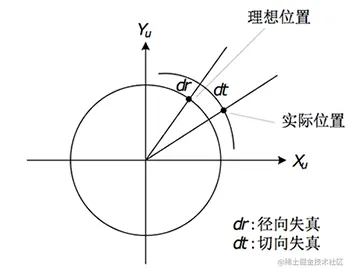
摄像机径向和切向畸变模型
对于归一化平面上的点(x,y,1) 由于畸变影响最终为 xdistorted,ydistorted
xdistorted=x1+k4r2+k5r4+k6r61+k1r2+k2r4+k3r6+2p1xy+p2(r2+2x2)
ydistorted=y1+k4r2+k5r4+k6r61+k1r2+k2r4+k3r6+2p2xy+p1(r2+2y2)
r2=x2+y2
对于廉价的网络摄像头,我们一般使用前两个径向畸变参数 k1 和 k2 就足够了。对于高度畸变的摄像机如鱼眼镜头,我们可以使用第三个径向畸变参数 k1,k2,k3
P′=MPw=⎣⎡m1m2m3⎦⎤Pw=⎣⎡m1Pwm2Pwm3Pw⎦⎤→(m3Pwm1Pw,m3Pwm2Pw)
这里
M=⎣⎡m1m2m3⎦⎤
这里要说的是任意给一个 M 我们是否能够判断
投影矩阵
- 什么样的矩阵 M 才是投影矩阵呢? 接下来我们就来看一看
M=K[RT]=[KRKT]=[Ab]
A=⎣⎡a1Ta2Ta3T⎦⎤
这里之所以写成 aiT 就是想将 ai 写成一个列向量,那么 M=(A,b) 为一个 3×4 的矩阵
- M 是透视投影矩阵的一个充分必要条件是 Det(A)=0
- M 是零倾斜透视投影矩阵的一个充分必要条件是 Det(A)=0 且满足