《Quantum Chemistry》（Levine）量子化学读书笔记003及第一章习题 P15-20

2023-05-21 167 阅读1分钟

复数

欧拉公式

对于一个虚数 $z=x+yi$ ，在坐标系中可表示为：

z=rcos\theta + ysin\theta

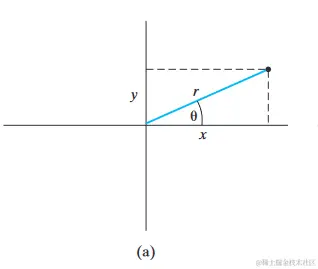
欧拉公式即可表示为：

e^{i\theta} = cos\theta + i\ sin\theta

它的共轭复数即为：

z^{*}=x-iy=re^{-i\theta}

习题

1.1 判断对错

所有光子都具有相同的能量。（×） $E=hv$
随着光频率的增加，波长减小。（√） $λ=\frac{c}{f}$
如果 $\lambda$ = 400 nm的紫光不会在某种金属中引起光电效应，那么可以肯定的是， $\lambda$ = 700 nm的红光不会在该金属中引起光电效应。（√）

1.29 验证下列各式

\sin \theta=\frac{e^{i \theta}-e^{-i \theta}}{2 i} , \quad \cos \theta=\frac{e^{i \theta}+e^{-i \theta}}{2}

解：对于第一个式子：

2i\,sin\theta = e^{i\theta }-e^{-i\theta } \\ 根据欧拉公式，2i\,sin\theta =cos\theta + i\,sin\theta - (cos\theta - i\,sin\theta)\\ 可得恒等式，2isin\theta = 2i sin\theta

对于第二个式子：

2\,cos\theta = e^{i\theta }+e^{-i\theta } \\ 根据欧拉公式，2\,cos\theta =cos\theta + i\,sin\theta + (cos\theta - i\,sin\theta)\\ 可得恒等式，2cos\theta = 2cos\theta