一、概述

对于下图所示的数据进行聚类，可以采用GMM或者K-Means的方法：

然而对于下图所示的数据，单纯的GMM和K-Means就无效了，可以通过核方法对数据进行转换，然后再进行聚类：

如果直接对上图所示的数据进行聚类的话可以考虑采用谱聚类（spectral clustering）的方法。

总结来说，聚类算法可以分为两种思路：

①Compactness，这类有 K-means，GMM 等，但是这类算法只能处理凸集，为了处理非凸的样本集，必须引⼊核技巧。

②Connectivity，这类以谱聚类为代表。

二、基础知识

1.无向权重图

谱聚类的方法基于带权重的无向图，图的每个节点是一个样本点，图的边有权重，权重代表两个样本点的相似度。

假设总共 $N$ 个样本点，这些样本点构成的图可以用 $G=(V,E)$ 表示，其中 $V=\left \{v_1,v_2,\cdots ,v_N\right \}$ ，图中的每个点 $v_i$ 也就代表了一个样本 $x_i$ ， $E$ 是边，用邻接矩阵（也是相似度矩阵） $W_{N\times N}$ 来表示， $W=[w_{ij}],1\leq i,j\leq N$ ，由于是无向图，因此 $w_{ij}=w_{ji}$ 。

另外还有度的概念，这里可以类比有向图中的出度和入度的概念，不过图中的点 $v_i$ 的度 $d_i$ 并不是和该点相连的点的数量，而是和其相连的边的权重之和，也就是邻接矩阵的每一行的值加起来，即：

$d_{i}=\sum_{j=1}^{N}w_{ij}$

而图的度矩阵（对角矩阵） $D_{N\times N}$ 可以表示如下：

$D=\begin{bmatrix} d_{1} & & &\\ & d_{2} & & \\& & ...& \\ & & & d_{N} \end{bmatrix}$

另外我们定义，对于点集 $V$ 的一个子集 $A\subset V$ ，我们定义：

$|A|:=子集A中点的个数\\ vol(A):=\sum _{i\in A}d_{i}$

2.邻接矩阵

构建邻接矩阵 $W$ 一共有三种方法，分别是 $\epsilon$ -近邻法、 $k$ 近邻法和全连接法。

$\epsilon$ -近邻法

首先需要设置一个阈值 $\epsilon$ ，比较任意两点 $x_i$ 与 $x_j$ 之间的距离 $s_{ij}=||x_{i}-x_{j}||_{2}^{2}$ 与 $\epsilon$ 的大小，定义邻接矩阵如下：

$w_{ij}=\left\{\begin{matrix} 0,s_{ij}>\epsilon\\ \epsilon ,s_{ij}\leq \epsilon \end{matrix}\right.$

这种方法表示如果两个样本点之间的欧氏距离的平方小于阈值 $\epsilon$ ，则它们之间是有边的。

使用这种方法，两点相似度只有 $\epsilon$ 和 $0$ 两个值，这种度量很不精确，因此在实际应用中很少使用 $\epsilon$ -近邻法。

$k$ 近邻法

使用KNN算法遍历所有样本点，取每个样本点最近的 $k$ 个点作为近邻。这种方法会造成构造的邻接矩阵不对称，而谱聚类算法需要一个对称的邻接矩阵。因此有以下两种方法来构造一个对称的邻接矩阵：

①只要一个点在另一个点的 $k$ 近邻内，则 $w_{ij}>0$ ，否则为 $0$ ，相似度 $w_{ij}$ 可以使用径向基函数来度量：

$w_{ij}=w_{ji}=\left\{\begin{matrix} exp\left \{-\frac{||x_{i}-x_{j}||_{2}^{2}}{2\sigma ^{2}}\right \},x_{i}\in KNN(x_{j})\; or \; x_{j}\in KNN(x_{i})\\ 0,x_{i}\notin KNN(x_{j})\; and\; x_{j}\notin KNN(x_{i}) \end{matrix}\right.$

②只有两个点互为 $k$ 近邻，才会有 $w_{ij}>0$ ，否则为 $0$ ：

$w_{ij}=w_{ji}=\left\{\begin{matrix} exp\left \{-\frac{||x_{i}-x_{j}||_{2}^{2}}{2\sigma ^{2}}\right \},x_{i}\in KNN(x_{j})\; and\; x_{j}\in KNN(x_{i})\\ 0,x_{i}\notin KNN(x_{j})\; or\; x_{j}\notin KNN(x_{i}) \end{matrix}\right.$

上述方法是不用先建立图而直接获得邻接矩阵，在编程实现时能够更加简便，构建的邻接矩阵也就表明了哪些样本点之间有边连接。也可以采用先建立图然后再在图上有边的数据点上保留权重获得邻接矩阵的方法。

全连接法

这种方法会使所有的 $w_{ij}$ 都大于 $0$ ，可以选择不用的核函数来度量相似度，比如多项式核函数、径向基核函数和 $sigmoid$ 核函数。最常用的是径向基核函数：

$w_{ij}=exp\left \{-\frac{||x_{i}-x_{j}||_{2}^{2}}{2\sigma ^{2}}\right \}$

在实际应用时选择全连接法建立邻接矩阵是最普遍的，在选择相似度度量时径向基核函数是最普遍的。

3.拉普拉斯矩阵

图的拉普拉斯矩阵（Graph Laplacian） $L_{N\times N}$ 是一个对称矩阵，用度矩阵减去邻接矩阵得到的矩阵就被定义为拉普拉斯矩阵， $L=D-W$ 。拉普拉斯矩阵有一些性质如下：

①对称性。
②由于其对称性，则它的所有特征值都是实数。
③对于任意向量 $f$ ，有：

$f^{T}Lf=\frac{1}{2}\sum_{i=1}^{N}\sum_{j=1}^{N}w_{ij}(f_{i}-f_{j})^{2}$

这一性质利用拉普拉斯矩阵的性质很容易可以得到：

$f^{T}Lf=f^{T}Df-f^{T}Wf \\ =\sum _{i=1}^{N}d_{i}f_{i}^{2}-\sum_{i=1}^{N}\sum_{j=1}^{N}w_{ij}f_{i}f_{j}\\ =\frac{1}{2}(\sum _{i=1}^{N}d_{i}f_{i}^{2}-2\sum_{i=1}^{N}\sum_{j=1}^{N}w_{ij}f_{i}f_{j}+\sum _{j=1}^{N}d_{j}f_{j}^{2})\\ =\frac{1}{2}(\sum_{i=1}^{N}\sum_{j=1}^{N}w_{ij}f_{i}^{2}-2\sum_{i=1}^{N}\sum_{j=1}^{N}w_{ij}f_{i}f_{j}+\sum_{i=1}^{N}\sum_{j=1}^{N}w_{ij}f_{j}^{2})\\ =\frac{1}{2}\sum_{i=1}^{N}\sum_{j=1}^{N}w_{ij}(f_{i}-f_{j})^{2}$

④拉普拉斯矩阵是半正定的，则其所有特征值非负，这个性质由性质③很容易得出。并且其最小的特征值为 $0$ ，这是因为 $L$ 的每一行和为 $0$ ，对于全 $1$ 向量 $1_{N}=\begin{pmatrix} 1 & 1 & \cdots & 1 \end{pmatrix}^{T}$ ，有 $L\cdot 1_{N}=0=0\cdot 1_{N}$ 。

4.无向图切图

对于无向图 $G$ 的切图，我们的目标是将 $G=(V,E)$ 切成相互没有连接的 $k$ 个子图，每个子图节点的集合为 $A_{1},A_{2},\cdots ,A_{k}$ ，它们满足 $A_{i}\cap A_{j}=\phi$ ，且 $A_{1}\cup A_{2}\cup \cdots \cup A_{k}=V$ 。

对于任意两个子图点的集合 $A,B\subset V$ ，定义 $A$ 和 $B$ 之间的切图权重为：

$W(A,B)=\sum _{i\in A,j\in B}w_{ij}$

对于 $k$ 个子图的集合，定义切图 $cut$ 为：

$cut(A_{1},A_{2},\cdots ,A_{k})=\sum_{i=1}^{k}W(A_{i}, \overline{A}_{i})$

上式中 $\overline{A}_{ i }$ 是 $A_{i}$ 的补集，意为除 $A_{i}$ 子集以外的其他子集的并集。

每个子图就相当于聚类的一个类，找到子图内点的权重之和最高，子图间的点的权重之和最低的切图就相当于找到了最佳的聚类。实现这一点的一个很自然的想法是最小化 $cut$ 。然而这种方法存在问题，也就是最小化的 $cut$ 对应的切图不一定就是符合要求的最优的切图，如下图：

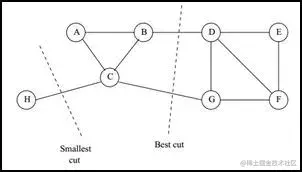
在上面的例子中，我们选择在最小的权重上进行切图，比如在 $C$ 和 $H$ 之间进行切图，这样可以使得 $cut$ 最小，但并不是最优的切图。

接下介绍谱聚类使用的切图方法。

三、模型定义

我们首先来做一些基本定义：

$样本X=\left(\begin{array}{llll}x_1 & x_2 & \cdots & x_N\end{array}\right)^{\top}=\left(\begin{array}{c}x_1^{\top} \\ x_1^{\top} \\ \vdots \\ x_N^{\top}\end{array}\right)_{N \times p}\\ 图G=\{V,E\}\;\;\;V代表顶点集合，E代表边集合\\ 顶点集V = \{1,2,...,N\}\; <=> \;X \;\;\; 每个顶点代表一个样本\\ 边集合E:W=[w_{ij}], 1≤i，j≤N\\ 其中:W:simiilarity \;matrix(affinity \;matrix)\\ w_{ij}=\left\{\begin{matrix} K(x_i,x_j)=exp\left \{-\frac{||x_{i}-x_{j}||_{2}^{2}}{2\sigma ^{2}}\right \},(i,j) \in E\\\ 0,(i,j) \in E \end{matrix}\right.$

谱聚类是基于Graph-based（带权重的无向图），因此我们将对该图所涉及到的一些变量进行具体定义。

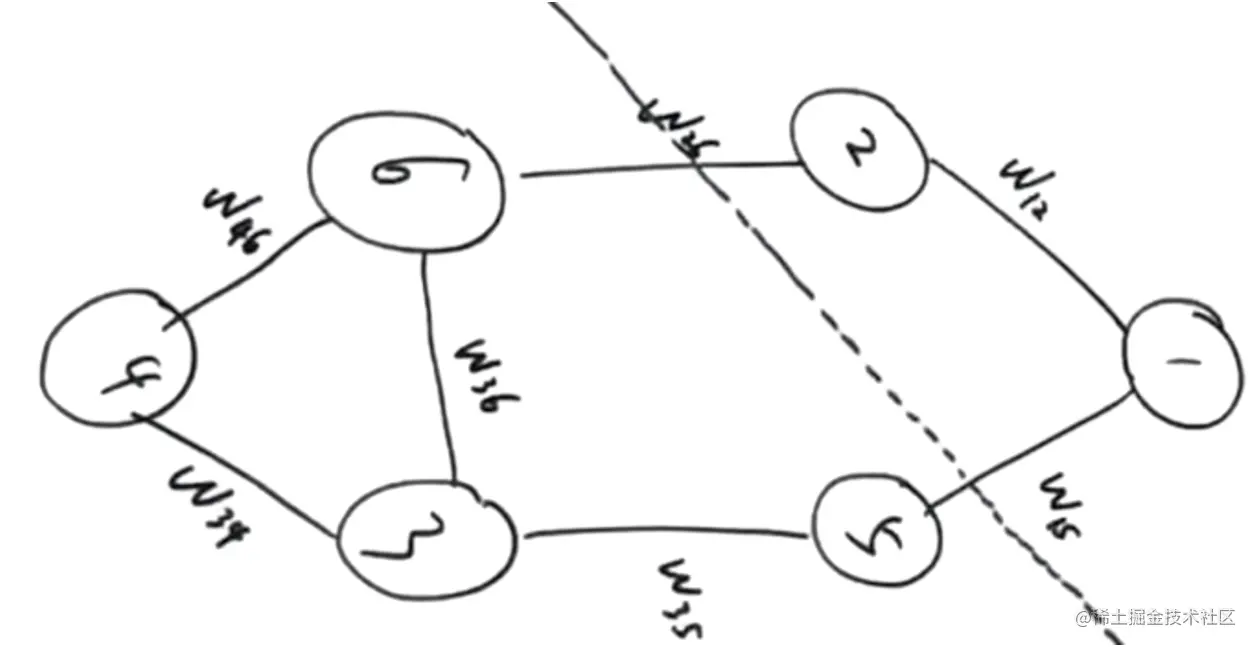
$定义：A ⊂ V，B ⊂ V， A ∩ B = ∅ ，\\ 在上图中，可以视作A即为点1,2；B为点3,4,5,6\\ W(A, B)=\sum_{\substack{i \in A \\ j \in B}} W_{i j}$

假如一共有K个类别，即 $\operatorname{cut}(V)=\operatorname{cut}\left(A_1, A_2, \cdots \cdot A_k\right)=\sum_{k=1}^K W\left(A_k, \bar{A}_k\right)=\sum_{k=1}^K W\left(A_k, V\right)-W\left(A_k, A_k\right)$ 在这里我们的目标是取得最小的Cut(V)，也就是让每一个类之间的关联度达到最低。

而 $cut(V)=degree(A_k)=\sum_{\substack{i ∈A_k\\}}di，d_i =\sum_{j=1}^N w_{i j}$ ， $di$ 就是在它所在类别中与它相连的顶点的相似矩阵之和，就比如，i=1时，因为1、2为一组，那么 $w_{ij}$ 最终的取值就只是 $w_{12}$ ，因为在相似矩阵的定义中别的地方的取值只能为0（不同组）

在这里有一个小问题，当同组的点个数越多，那么相似矩阵之和必然越多，即我们需要保证不会因为数量问题使得后续优化问题的结果取向局部最优，因此最好的方式是在每一组下面除以一个当前组数，求平均，即最终的目标转化为： $min\;Ncut(V)$

\begin{aligned} Ncut & =\sum_{k=1}^K \frac{W\left(A_k, \bar{A}_k\right)}{\sum_{i \in A_k} d_i} \\ \end{aligned}

四、模型的矩阵形式

定义指示向量(indicator vector)： $\left\{\begin{array}{l} y_i \in\{0,1\}^k \\ \sum_{i=1}^k y_{i j}=1 \end{array}\right. \\$ $1 \leqslant i \leqslant N ,\;\; 1 \leqslant j \leqslant k$ 这样表示的意思就是one-hot向量，对于第 $i$ 个样本而言，它属于第 $j$ 个类别。

我们现在考虑将上述 $Ncut$ 模型转换为矩阵形式，定义 $Y=(y_1,y_2,..,y_N)^T_{N*k} 则\;\;\hat{Y}=\underset{Y}{\operatorname{argmin}} N_{\text {cut }}(v)$ 其实就相当于引入一个 $Y$ 矩阵，其中 $yi$ 是 $k$ 维one-hot向量，因为每个样本 $i$ 只属于一个类别，只能一个维度为1。

由于优化问题的结果，一定是一个实数，所以我们可以考虑将 $Ncut$ 转化为矩阵，并对其求 $trace$ ，其过程如下所示，将原式拆解成O、P两部分：

$\begin{aligned} & N_{\text {cut }}(v)=\sum_{k=1}^K \frac{W\left(A_k, \bar{A}_k\right)}{\sum_{i \in A_k} d_i}\color{red}=\operatorname{tr} O \cdot P^{-1} \\ & \left.=\operatorname{tr}\left(\begin{array}{cc} W\left(A_1, \bar{A}_1\right) & &&\\ &W\left(A_2, \bar{A}_2\right)& &&\\ & &\ddots \\ &&&W\left(A_k, \bar{A_k}\right)& \end{array}\right)\right \} \color{red}O_{k×k} \\ & \text { . } \left.\left(\begin{array}{ccc} \sum_{i \in A_1} d_i & & &\\ & \sum_{i \in A_2} d_i & &\\ & & \ddots & \\ & & &\sum_{i \in A_k} d_i \end{array}\right)^{-1}\right\} \color{red}P_{k×k} \\ & \end{aligned}$

P的含义： $A1，A2...$ 都属于一个样本子集，求和 $d_i$ 意味着对于每一个子集内每一个点的度求和，假如 $A_1=\{1,2,5\}$ ，那么 $P_{1,1}=d1+d2+d5$

我们再来回顾一下，现在我们已知的是W，Y，要求的是O，P，并且选择从P开始入手。由于W是一个很正常的矩阵，我们现在考虑从Y入手看看有没有什么新发现。

对于 $Y=(y_1,y_2,..,y_N)^T_{N*k}$ 而言， $Y^TY=\sum_{i=1}^Ny_i \cdot y_i^T$ ，为k × k 维的矩阵，将其展开得到式子 $y_1 y_1^{\top}+\cdots y_N y_N{ }^{\top}$ ，且，根据定义，如果 $y_{1k}=1,y_{2k}=1$ 就代表着样本 $x1,x2∈A_k$ ，将此概念广泛化，即为：

$N_k$ : 在N个样本中，属于类别 $k$ 的样本个数
$\sum_{k=1}^k N_k=N, \quad N_k=\left|A_k\right|=\sum_{i \in A_k} \cdot 1$

这个结论与P的对角线某一项如此的相似，由此，我们可以作进一步转化。

$Y^TY=\left(\begin{array}{llll}N_{1} & & &\\ & N_{2} & & \\& & ...& \\ & & & N_{k} \end{array}\right)_{k ×k}\color{red}=\left(\begin{array}{llll}\sum_{i \in A_1} 1 & & &\\ & \sum_{i \in A_2} 1 & &\\ & & \ddots & \\ & & &\sum_{i \in A_k} 1 \end{array}\right)\\ \begin{aligned} & P=\left(\begin{array}{llll}\sum_{i \in A_1} d_i & & &\\ & \sum_{i \in A_2} d_i & &\\ & & \ddots & \\ & & &\sum_{i \in A_k} d_i \end{array}\right) =Y^{\top} \cdot D \cdot Y \\ & 其中: D=\left(\begin{array}{llll} d_1 & & & \\ & d_2 & \\ && \ddots \\ & & &d_N \end{array}\right)=\operatorname{diag}\left(W \cdot 1_{N × 1}\right) \\ & diag() 即将W \cdot 1_{N × 1}的结果(N × 1的列向量)转化为对角线上的值，构造N × N的对角矩阵 \end{aligned}$

到这里我们就求得了P，接下来试着将O进行表达，首先对 $O_{k,k}$ 进行解读

$\begin{aligned} O_{k,k}= & W\left(A_K, \bar{A}_K\right) \\ & =\underbrace{W\left(A_k, v\right)}_{\sum_{i \in A_k} d_i}- \underbrace{W\left(A_k, A_k\right)}_{\sum_{i \in A_k, j \in A_k} w_{i j}} \\ \end{aligned}$

自然而然的，我们可以将O改写成如下形式，并且左项已在P时就求得，牢牢抓住已知条件只有W，Y，右项则需要进一步尝试

$O=\left(\begin{array}{llll}\sum_{i \in A_1} d_i & & &\\ & & \ddots & \\ & & &\sum_{i \in A_k} d_i \end{array}\right)-\left(\begin{array}{llll} w(A_1,A_1)&&\\ &\ddots&\\ && w(A_k,A_k) \end{array}\right)\\ =Y^{\top} D Y-△ \\$

由于右项与w相关，且 $Y^TY$ 又能构造相同维度矩阵，不难得出应该尝试一下 $Y^TWY$

$Y^{\top} W Y=\left(\begin{array}{llll} \sum_{i \in A_{1}} \sum_{j \in A_{1}} w_{i j}&\sum_{i \in A_{1}} \sum_{j \in A_{2}} w_{i j}&\cdots&\sum_{i \in A_{1}} \sum_{j \in A_{K}} w_{i j}\\ \vdots&&&\vdots\\ \sum_{i \in A_{K}} \sum_{j \in A_{1}} w_{i j}&\cdots&\cdots&\sum_{i \in A_{K}} \sum_{j \in A_{K}} w_{i j} \end{array}\right)$

与△有些许不同，故我们可以定义 $O^{’}=Y^{\top} D Y-Y^TWY$

这无伤大雅，因为我们的目标是求 $Ncut(v)$ ，且 $P$ 为对角矩阵，则 $tr\;O^{’} \cdot P^{-1}=tr\;O \cdot P^{-1}$

到了这里，我们就求得了我们的最终目标：

$\hat{Y}=\operatorname{argmin}_Y \operatorname{tr}\left(Y^{\top}(D-w) Y \cdot\left(Y^{\top} D Y\right)^{-1}\right)\\ 其中：L=D-w就是著名的 Laplacian \;Matrix$

五、总结

谱聚类是一种在数据集中找出群集或者组的技术。与传统的聚类算法（如K-means）相比，谱聚类可以识别出复杂的聚类结构，并且不需要事先假设每个群集在几何形状上的均匀性。谱聚类的工作原理是将数据点转化为图形结构，然后通过对图形进行操作（例如切割图形以最小化连接不同组的边的权重）来识别出组。

下面是谱聚类的基本步骤：

构建相似性矩阵：对于输入的数据点，计算每对数据点之间的相似性，并形成一个相似性矩阵。
构建图：基于上一步的相似性矩阵，构建一个图，其中每个节点代表一个数据点，每个边代表两个数据点的相似度。
构建拉普拉斯矩阵：然后计算出所谓的拉普拉斯矩阵。拉普拉斯矩阵是图的一个关键属性，可以反映出图的结构信息。常见的拉普拉斯矩阵有无向图的拉普拉斯矩阵和归一化拉普拉斯矩阵等。
计算拉普拉斯矩阵的特征向量和特征值：然后求解拉普拉斯矩阵的特征向量和特征值。
基于特征向量进行聚类：选择前k个最小的特征值对应的特征向量，将它们按列合并成一个矩阵，然后将这个矩阵的每一行看作是原数据在新的空间下的表示，对这些数据点使用传统的聚类方法（如K-means）进行聚类。

谱聚类的优点是能够处理复杂的非线性数据，并且可以识别出复杂的聚类结构。但是，谱聚类的计算成本可能会比较高，尤其是对于大型数据集，因为需要计算和存储全量的相似度矩阵，并对其进行特征分解。

24.谱聚类：一种超越K-means的聚类方法