经典力学

根据牛顿经典力学，粒子的运动规律符合牛顿第二定律:

F=ma=m\frac{d^{2}x}{dt^{2}} \tag{1}

推导过程如下：

a=\frac{dv}{dt}=\frac{d}{dt}\frac{dx}{dt}=\frac{d^{2}x}{dt^{2}} \tag{2} \\ F=ma=m\frac{d^{2}x}{dt^{2}}

对于，经典力学中一个一维粒子的势能 V，

\frac{\partial V(x,t)}{\partial x} =-F(x,t) \tag{3}

含时薛定谔方程（Time-Dependent Schrödinger Equation）

假设一个波函数 $\Psi$ 可以描述量子状态的粒子，那么对于单个、一维的粒子，则有 $\Psi=\Psi(x,t)$ ，该方程假设为：

-\frac{\hbar}{i} \frac{\partial \Psi(x, t)}{\partial t}=-\frac{\hbar^{2}}{2 m} \frac{\partial^{2} \Psi(x, t)}{\partial x^{2}}+V(x, t) \Psi(x, t) \tag{1}

其中， $\hbar=\frac{h}{2\pi}$ ， $i=\sqrt{-1}$ ， $m$ 为质量， $V(x, t)$ 为体系势能函数。

根据“玻恩定则”（Born rule），对于一个单粒子、一维系统： $|\Psi(x, t)|^{2} dx$ 可以给出在时间 $t$ 在 x 轴位于 $x$ 和 $x + dx$ 之间的区域中找到粒子的概率。函数 $|\Psi(x, t)|^{2}$ 是在 x 轴上的不同位置找到粒子的概率密度。

这是一个基础公设，目前没有明确的解释为什么波函数的模的平方就是概率密度¹。

对于一个单粒子、一维系统，波函数用高斯波包表示²:

\psi (x,t) = \frac{1}{(2\pi\sigma_x^2)^{1/4} \sqrt{1 + \frac{ \mathrm{i} \hbar t}{2m \sigma_x^2}}} \exp \left[\frac{-(x - x_0 - \frac{p_0 t}{m})^2}{(2\sigma_x )^2 \left(1 + \frac{ \mathrm{i} \hbar t}{2m \sigma_x^2} \right) } \right] \exp \left[\frac{ \mathrm{i} p_0}{\hbar } \left(x - \frac{p_0 t}{2m} \right) \right] \tag{2}

t = 0，\psi (x,0) = \frac{1}{(2\pi\sigma_x ^2)^{1/4}} \mathrm{e} ^{-(x - x_0)^2/(2\sigma_x)^2} \mathrm{e} ^{ \mathrm{i} \frac{p_0}{\hbar}x} \tag{3}

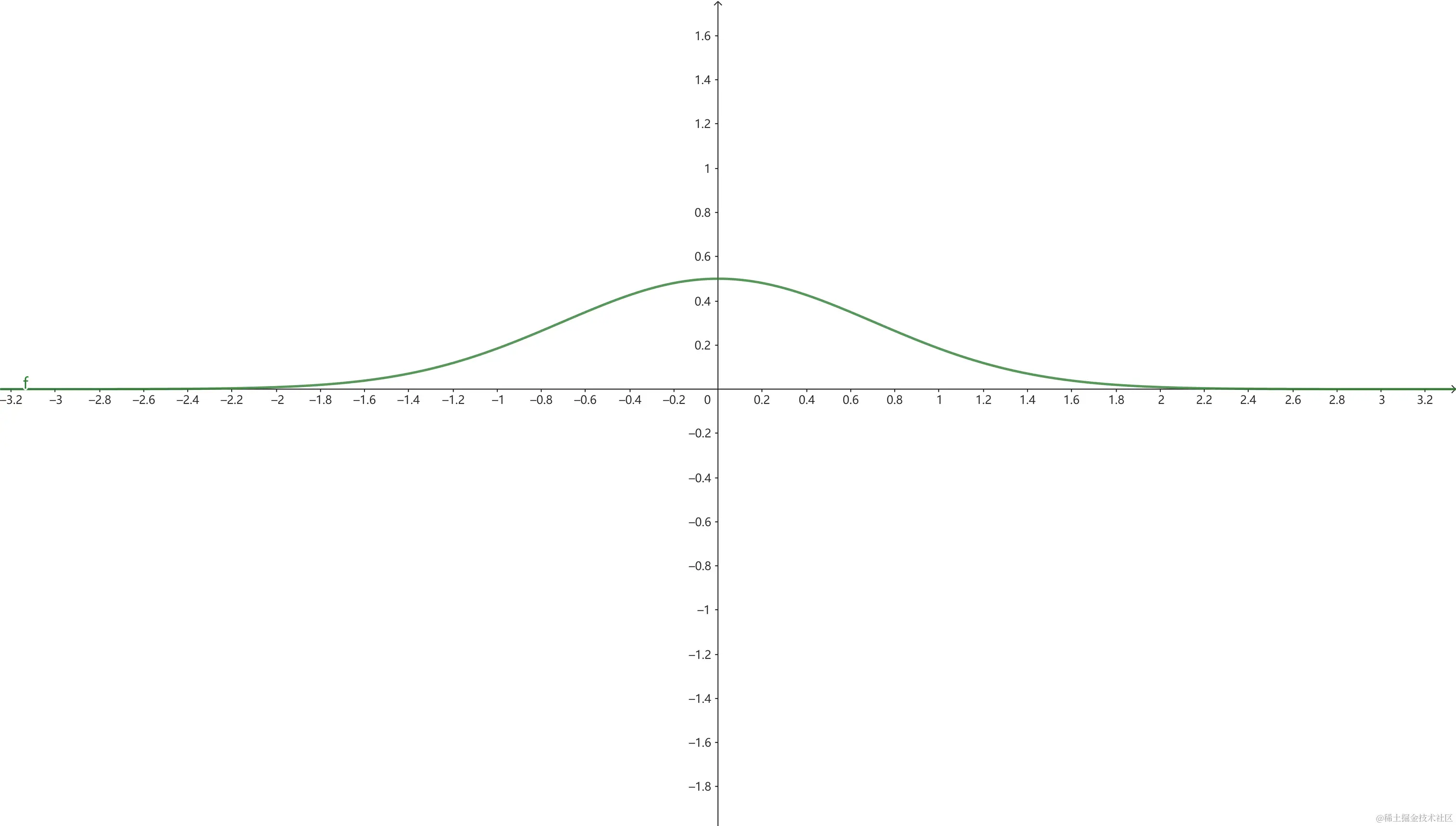
由式(2)可知，对于一个固定时间 $t_{0}$ ，我们可以假设，波函数为 $ae^{-bx^{2}}$ （ $a$ ， $b$ 为常数），则有概率密度函数： $a^{2}e^{-2bx^{2}}$ 。据此，我们可知在 $x=0$ 更有可能观察到粒子。因为无论 $a$ 和 $b$ 如何变化，都有类似趋势：

《Quantum Chemistry》（Levine）读书笔记002 P7-10

经典力学

含时薛定谔方程（Time-Dependent Schrödinger Equation）