对比学习系列（一）---InfoDisc作者揭示了一种典型的区分性学习方法能够自动发现语义类别之间的明显相似性，而无需额

前言

在ImageNet数据集上，top-5分类错误率明显比top-1分类错误率低。普遍地，对于某一输入图像，其softmax输出概率对应的第二类别通常与第一类别视觉上相似。如上图所示，输入图像中有一只豹子（leopard）,类别为豹子（leopard）类，观察它的分类输出，这张图片前四的类别分别是豹子（leopard），美洲豹（jaguar），猎豹（cheetah）和雪豹（snow leopard）。而且我们会发现美洲豹（jaguar）类别对应的概率值要高于书架（bookcase）类别对应的概率值。从展示的示例图片上看，不同豹类图片之间的图片相似性较高，豹子和救生艇（lifeboat），购物车（shopcart）和书架（bookcase）类别之间明显存在很高的差异性。

通过这些观察，作者揭示了一种典型的区分性学习方法能够自动发现语义类别之间的明显相似性，而无需额外指导。也就是说，表面相似性不是从语义注释中获得的，而是从视觉数据本身获得的。

将类别扩展到实例，那么能否仅仅通过要求特征区分单个实例学习到一个能捕捉实例之间的明显相似性的特征表示？一个图像本身是独特的，每个图像都可能与来自于同一语义范围的其图像有显著的差异。如果不需要类别语义信息区分单个图像，学习到的特征捕捉到实例之间的相似性，类似于类别监督学习特征学习到特征之间的相似性。

方法

我们的目标是学习一个无监督的嵌入函数 $v = f \left( \theta \right)$ 。 $f_{\theta}$ 是参数为 $\theta$ 的深度学习网络，输入图像为 $x$ ，输出特征为 $v$ 。此嵌入会在图像空间上产生一个度量，对于实例x和y，记为 $d_{\theta}\left( x, y \right) = \| f_{\theta}\left( x \right) - f_{\theta}\left( y \right) \|$ 。一个好的嵌入应当将视觉上相似的图像映射到彼此相近的位置。

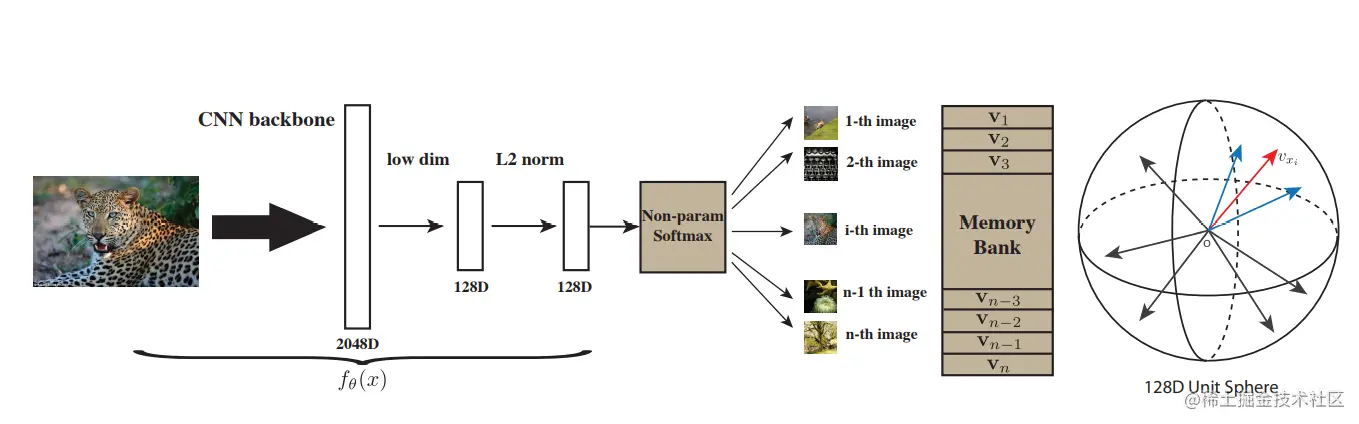
假设有 $n$ 个图像 $x_{1}, \cdots, x_{n}$ ， $n$ 个类别，它们的特征分别为 $v_{1}, \cdots, v_{n}$ 。对于图像 $x$ ，其特征为 $v = f_{\theta}\left(x\right)$ ，使用softmax函数进行instance-level分类，它被识别为第 $i$ 类的条件概率如下所示：

P\left( i | v \right) = \frac{exp\left( w_{i}^{T}v \right)}{\sum_{j=1}^{n}exp\left( w_{j}^{T}v\right)} \quad \quad \quad \left(1\right)

$w_{j}$ 为类别 $j$ 的权重向量和 $w_{j}^{T}v$ 计算 $v$ 和第 $j$ 类的匹配程度。其中 $w_{j}$ 是需要被学习的参数，我们称之为有参数的分类器。softmax参数分类的问题在于权重向量 $w_{j}$ 作为类别原型，阻止了实例之间的比较。论文中使用 $v_{j}^{T}v$ 替代 $W_{j}^{T}v$ ，通过L2正则化层使得 $\| v \| = 1$ ，那么实例 $x$ 被识别成第 $i$ 类的条件概率如下所示

P\left( i | v \right) = \frac{exp\left( v_{i}^{T}v / \tau\right)}{\sum_{j=1}^{n} exp \left( v_{j}^{T}v / \tau \right)} \quad \quad \quad \left(2\right)

其中 $\tau$ 是温度参数，控制着分布的concentration level。公式（2）没有要学习的参数变量，称为无参数的softmax分类器。

学习的目标函数为最大化联合概率 $\prod_{i=1}^{n} P_{\theta} \left( i | f_{\theta} \left( x_{i} \right) \right)$ ，或者等价于最小化对数似然的负数。

J \left( \theta \right) = - \sum_{i=1}^{n} log P \left( i | f_{\theta} \left( x_{i} \right) \right)

为了计算公式2中的概率 $P\left( i | v \right)$ ，所有图片的 $v_{j}$ 是需要的。为了不用每次穷尽地计算这些表示，论文维护了一个储存图片特征的memory bank。假设 $V=\{v_{j}\}$ 为memory bank， $f_{i} = f_{\theta} \left( x_{i} \right)$ 为 $x_{i}$ 的特征。在每次学习迭代中，表示 $f_{i}$ 和网络参数 $\theta$ 通过SGD进行优化，然后 $f_{i}$ 在相应的实例条目 $f_{i} \rightarrow v_{i}$ 处更新 $V$ 。初始化memory bank $V$ 的所有表示为单位随机向量（unit random vectors）。

NCE

对于ImageNet-1k数据集来说，120万张图片和1000个类别。但是对于instance-level，每个图像都是一类，则有120万类。

公式2的无参数softmax，需要计算与训练集中的所有实例之间的相似性，当 $n$ 比较大的时候，计算成本较高。论文使用NCE（noise-contrastive estimation）解决这个问题。基本思想是将多类分类问题转换成一组二分类问题。其中二分类任务区分数据样本和噪声样本。在memory bank中特征表示 $v$ 与第 $i$ 个样本关联的概率为：

P\left( i | v \right) = \frac{exp\left( v^{T} f_{i} / \tau \right)}{Z_{i}} \\ Z_{i} = \sum_{j=1}^{n} exp \left( v_{j}^{T} f_{i} / \tau \right) \quad \quad \quad \left(3\right)

其中 $Z_{i}$ 是归一化常数。假设噪声分布为 $P_{n}=1/n$ ，并且噪声样本是数据样本的 $m$ 倍。那么对于来自于数据分布的样例 $i$ ，特征为 $v$ 的后验概率为：

h\left( i，v \right) = P\left( D=1|i,v \right) = \frac{P\left( i | v \right)}{P\left( i | v\right) + m P_{n}\left( i \right)}

近似训练目标是最小化数据样本和噪声样本的log后验分布的负数。公式如下：

J_{NCE} \left( \theta \right) = -E_{P_{d}} [ log h\left( i, v \right) ] - m \cdot E_{p_{n}} [log \left( 1 - h\left( i, {v}' \right) \right)]

其中 $P_{d}$ 表示数据分布。对于 $P_{d}$ ， $v$ 是 $x_{i}$ 的特征；对于 $P_{n}$ ， ${v}'$ 是从噪声分布 $P_{n}$ 随机抽样的样本的特征。对于论文中的模型， $v$ 和 ${v}'$ 都是从无参数memory bank中抽样得到的。

计算公式3中的正则常量 $Z_{i}$ 消耗较大，借鉴其他论文的方法，将它看做一个常量，通过Monte Carlo 近似方法估计它的值。

Z \simeq Z_{i} \simeq nE_{j} [exp\left( v_{j}^{T} f_{i} / \tau \right)] = \frac{n}{m}\sum_{k=1}^{m}exp\left( v_{j_{k}}^{T} f_{i} / \tau \right)

其中 $j_{k}$ 是下标的随机子集，NCE将每个样例的计算复杂度从 $O\left( n \right)$ 降到 $O\left( 1 \right)$ 。

Proximal Regularization

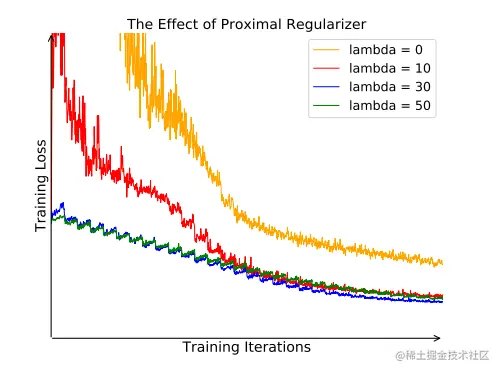
论文中的模型是instance-level的分类器，不同于常见的分类模型，每个类别有多张图片，instance-level模型每个类别一张实例。在训练过程中，每个类别仅仅被观察一次。那么学习过程会因为随机抽样而波动很大。论文采用proximal regularization的方法，通过添加迭代参数 $t$ ，平滑训练过程。

设当前迭代为 $t$ ，数据 $x_{i}$ 的特征表示为 $v_{i}^{\left( t \right)} = f_{\theta}\left( x_{i} \right)$ ，前一个迭代的特征内存库为 $V=\{v^{\left( t -1 \right)} \}$ ，那么一个正样本（来自 $P_{d}$ 分布）的损失函数为：

-log h \left( i, v_{i}^{\left( t-1 \right)} \right) + \lambda \| v_{i}^{\left( t\right)} - v_{i}^{\left( t-1 \right)} \|_{2}^{2}

随着学习的迭代，迭代之间的差异，逐渐消失，增加的损失减少到原先的损失。加入proximal regularization之后的目标方程为：

\begin{matrix} J_{NCE} \left( \theta \right) =& -E_{P_{d}} [ log h\left( i, v_{i}^{\left( t-1 \right)} \right) - \lambda \| v_{i}^{\left( t\right)} - v_{i}^{\left( t-1 \right)} \|_{2}^{2}] \\ &- m \cdot E_{p_{n}} [log \left( 1 - h\left( i, {v}'^{\left( t-1 \right)} \right) \right)] \end{matrix}

Weighted k-Nearest Neighborhood Classification

对于一个测试图片 $\hat{x}$ ，首先计算它的特征 $\hat{x} = f_{\theta}\left( \hat{x} \right)$ ，然后使用余弦相似度 $s_{i} = cos\left( v_{i}, \hat{f}\right)$ 与memory bank中的所有图片嵌入特征进行比较，最相似的k个邻居，表示为 $N_{k}$ ，最后通过加权投票的方式进行预测。

假设预测的类别为 $c$ ，类别 $c$ 的总权重为 $\omega_{c} = \sum_{i \in N_{k}}\alpha_{i} * 1\left( c_{i} = c\right)$ 。其中 $\alpha_{i} = exp\left( s_{i} / \tau \right)$ 是邻居 $x_{i}$ 的贡献度。论文在训练时选择 $\tau=0.07$ ，并且设 $k=200$ 。