三角形的移动、旋转和缩放
在编写css的动画时,我们能够接触到translate,rotate,scale,现在我们来探究下这些动画背后的数学知识,以及如何把这些知识运用到webgl的图像变换上。
平移
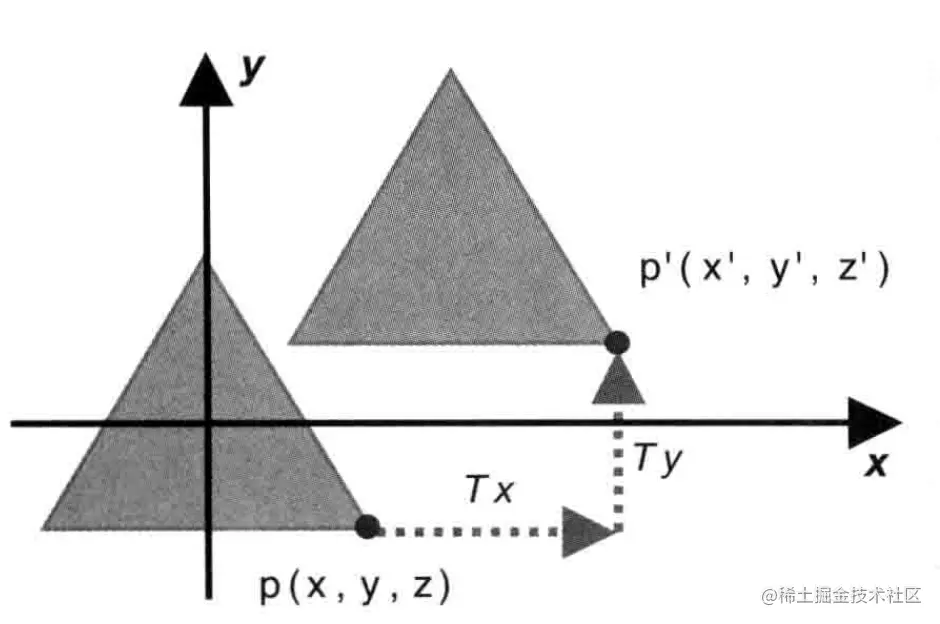
当我们把点p(x, y ,z)移动到点p'(x', y', z'),那么点p在X轴,Y轴,Z轴的平移距离我们分别设为Tx,Ty,Tz。那么我们可以得到以下公式:
x′=x+Txy′=y+Tyz′=z+Tz
旋转
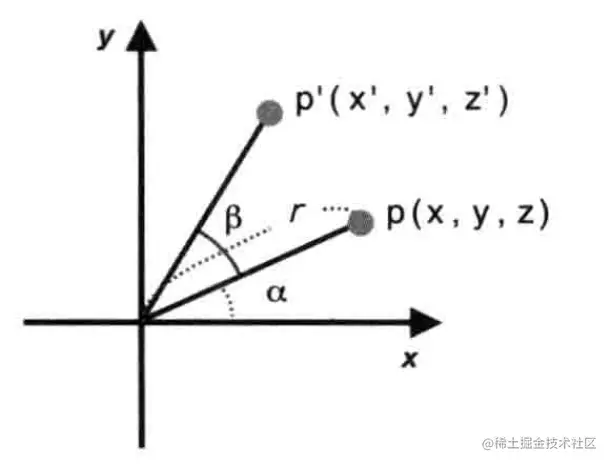
这里我们先用二维平面中的旋转来解释。假设r是从原点到点p的距离,而α是X轴旋转到点p的角度。根据这个条件,能得出式子1:
x=rcosαy=rsinα
现在p点的坐标是(x,y,z),假设我们向上旋转了β角度,得到点p'(x',y',z'),那么我们能够得到式子2:
x′=rcos(α+β)y′=rsin(α+β)z′=z
之后我们根据三角函数两角和公式,可推出式子3:
a=r(cosαcosβ−sinαsinβ)b=r(sinαcosβ+cosαsinβ)
然后我们把式子1代入式子3,得出式子4:
x′=xcosβ−ysinβy′=xsinβ+ycosβz′=z
缩放
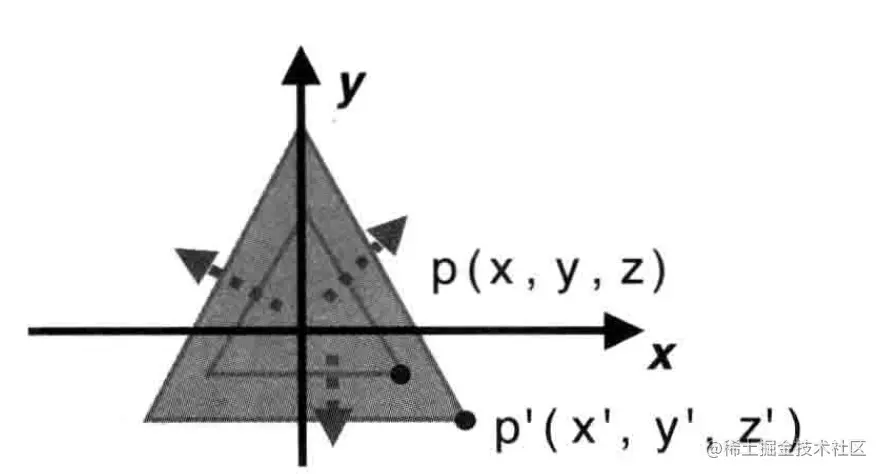
假设在三个方向X轴,Y轴,Z轴的缩放因子为Sx,Sy,Sz,那么有式子:
x′=Sxxy′=Syyz′=Szz
变换矩阵
其实上面的这些变换公式,都能用统一的格式来表示,那就是矩阵。矩阵乘法要求我们要用第一个矩阵的行去乘第二个矩阵的列,下面我们以平移的公式来推导出平移矩阵。
平移矩阵
在平移时,我们已经推出了以下公式:
x′=x+Txy′=y+Tyz′=z+Tz
现在我们把它扩充成齐次坐标的形式。
x′=ax+by+cz+dy′=ex+fy+gz+hz′=ix+jy+kz+l1=mx+ny+oz+p
转成矩阵相乘的形式:
⎣⎡x′y′z′1⎦⎤=⎣⎡aeimbfjncgkodhlp⎦⎤∗⎣⎡xyz1⎦⎤
根据齐次坐标的定义,一个点(或者说一个矢量)有四个因子(x,y,z,w)。这里我们的w固定是1,在变换矩阵中最下一行永远是[0,0,0,1],即上式中的m,n,o均为0,p为1。对比x′=ax+by+cz+d和x′=x+Tx,我们得出a,b,c均为0,d为Tx。经过最终的推导,我们得出平移矩阵为:
⎣⎡100001000010TxTyTz1⎦⎤
旋转矩阵
旋转矩阵和缩放矩阵的推导过程同理,不赘述。
⎣⎡cosβsinβ00−sinβcosβ0000100001⎦⎤
缩放矩阵
⎣⎡Sx0000Sy0000Sz00001⎦⎤
吐槽一下,在markdown里写公式是真的麻烦!
参考