Step 1: Function set

Target: $P_{w, b} (C_1|x)$

• If target >= 0.5, output $C_1$
• Else, output $C_2$

Based on previous knowledge in juejin.cn/post/722520…

• $P_{w, b} (C_1|x) = \sigma(z) = \frac{1}{1 + exp(-z)}$
• $z = wx + b = \sum_i w_i x_i + b$

Function set: $\{f_{w, b} (x) = P_{w, b} (C_1|x), \forall w, \forall b\}$

Step 2: Goodness of a function

Training data: $\{(x_1, C_1), (x_2, C_1), (x_3, C_2),\dots, (x_N, C_1)\}$

• Given w & b, its probability of generating the training data

$L(w, b) = f_{w, b}(x^1) f_{w, b}(x^2) (1 - f_{w, b}(x^3)) \dots f_{w, b}(x^N)$

• Find the w & b with maximum probability

$w^*, b^* = \arg \max_{w, b} L(w, b) = \arg \min_{w, b} -ln L(w, b)$

• Define $\hat{y}^n$: 1 for $C_1$, 0 for $C_2$

$- ln L(w, b) = - \sum_n (\hat{y}^n ln f_{w, b} (x^n) + (1 - \hat{y}^n) ln f_{w, b} (x^n) )$ -- cross entropy between two Bernoulli distributions

Step 3: Find the best function

Gradient descent:

• $\frac{\partial -ln L(w, b)}{ \partial w_i} = \sum_n -(\hat{y}^n - f_{w, b} (x^n)) x_i^n$ -- larger difference, larger update

Discussions

Compare with linear regression

Why not square error in loss function?

$\frac{\partial L}{\partial w_i} = \frac{\partial (f_{w, b}(x) - \hat{y})^2} {\partial w_i} = 2 (f_{w, b}(x) - \hat{y}) f_{w, b}(x) (1 - f_{w, b}(x)) x_i$

When $\hat{y}^n = 1$, (similar when 0)

• If $f_{w, b}(x^n) = 1$, close to target, $\frac{\partial L}{\partial w_i} = 0$
• If $f_{w, b}(x^n) = 0$, far from target, $\frac{\partial L}{\partial w_i} = 0$ -- update slow

Cannot tell close to / far from target with small $\frac{\partial L}{\partial w_i}$

Discrimitive v.s. Generative

See the generative method in juejin.cn/post/722520…

Differnt function because of different assumptions

• in the generative model: distribution assumption, naive bayes, etc.

Usually discrimitive model has a better performance

Limitation of logistic regression

Linear boundary -> feature transformation

How to find a good transformation? -> cascading logistic regression models -- neural network

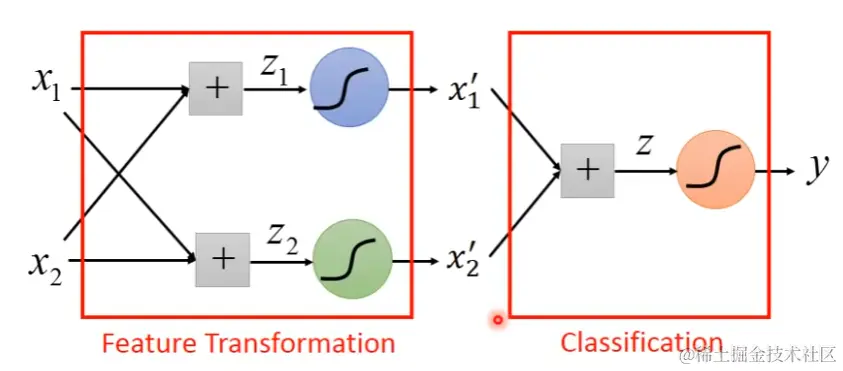
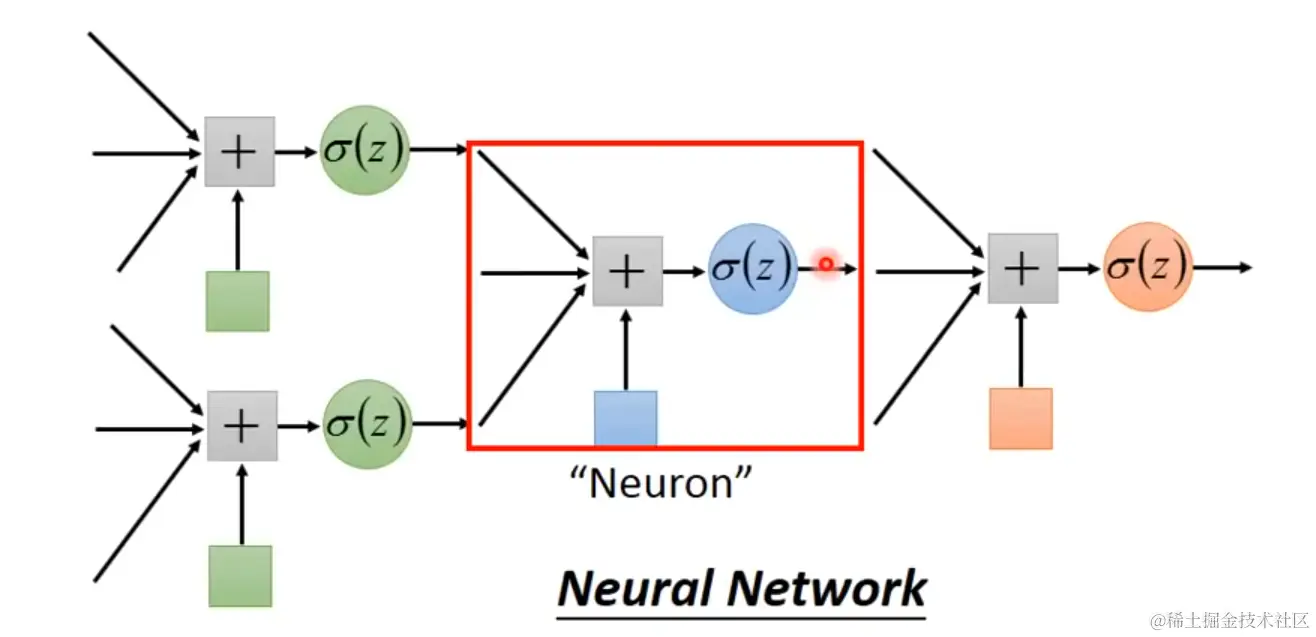
Multi-class classification

Softmax: $y_i = P(C_i | x) = e^{z_i} / \sum_j e^{z_j}$, where $z_i = w_i x + b_i$

• $0 < y_i < 1$
• $\sum_i y_i = 1$

Cross entropy: $- \sum_i \hat{y}_i ln y_i$

• $\hat{y} = (\hat{y}_1, \hat{y}_2, \dots )$ - target
• If $x \in C_1$, $\hat{y} = (1, 0, 0, \dots )$