动态规划二：单序列

1. 爬楼梯

class Solution {
    // 动态转移方程: dp[i] = dp[i-1] + dp[i-2]
    public int climbStairs(int n) {
        if (n < 3) {
            return n;
        }
        int[] dp = new int[n + 1];
        dp[1] = 1;
        dp[2] = 2;
        for (int i = 3; i <= n; i++) {
            dp[i] = dp[i - 1] + dp[i - 2];
        }
        return dp[n];
    }
}

2. 斐波那契数

class Solution {
    // 动态转移方程: dp[i] = dp[i-1] + dp[i-2]
    public int fib(int n) {
        if (n < 2) {
            return n;
        }
        int[] dp = new int[n + 1];
        dp[0] = 0;
        dp[1] = 1;
        for (int i = 2; i <= n; i++) {
            dp[i] = dp[i - 1] + dp[i - 2];
        }
        return dp[n];
    }
}

3. 解码方法(常考题)

class Solution {
    // 如果字符串的第i位和i-1位能组成[10,26]中的数字,说明我们可以在i-2的位置上继续解码
    public int numDecodings(String s) {
        int n = s.length();
        if (n == 0) {
            return 0;
        }
        int[] dp = new int[n + 1];
        // 注意：这里一定写成1,第0位不存在，是为了两位数字转换如果有效算一种情况dp[2] += dp[0],需要算一种情况
        dp[0] = 1;
        dp[1] = s.charAt(0) == '0' ? 0 : 1;
        for (int i = 2; i <= n; i++) {
            int twoDigit = Integer.valueOf(s.substring(i - 2, i));
            int oneDigit = Integer.valueOf(s.substring(i - 1, i));
            if (10 <= twoDigit && twoDigit <= 26) {
                dp[i] += dp[i - 2];
            }
            if (oneDigit != 0) {
                dp[i] += dp[i - 1];
            }
        }
        return dp[n];
    }
}

4. 单词拆分

class Solution {
    public boolean wordBreak(String s, List<String> wordDict) {
        // 状态:dp[i]表示s[0,i-1]子串能否被字典中的单词拼出
        int n = s.length();
        boolean[] dp = new boolean[n + 1];
        // 初始化: i=0,即s长度为0,默认为true
        dp[0] = true;
        for (int i = 1; i <= n; i++) {
            for (int j = 0; j < i; j++) {
                if (dp[j] && wordDict.contains(s.substring(j, i))) {
                    dp[i] = true;    // (0,j-1) && (j,i-1)=true
                }
            }
        }
        return dp[n];
    }
}

5. 单词拆分 II

class Solution {
    public List<String> wordBreak(String s, List<String> wordDict) {
        int n = s.length();
        List<String> res = new ArrayList<>();
        // 直接设置dp为List
        List<Integer>[] dp = new ArrayList[n + 1];
        // 初始化: dp[i]表示哪些位置j可以到达i位置
        for (int i = 0; i <= n; i++) {
            dp[i] = new ArrayList<>();
        }
        dp[0].add(0);
        for (int i = 1; i <= n; i++) {
            for (int j = 0; j < i; j++) {
                if (!dp[j].isEmpty() && wordDict.contains(s.substring(j, i))) {
                    dp[i].add(j);
                }
            }
        }
        // 递归处理结果
        dfs(s, res, n, dp, "");
        return res;
    }

    private void dfs(String s, List<String> res, int index, List<Integer>[] dp, String cur) {
        if (index == 0) {           // 设置边界:到index=0,一条路径就拼接完成了
            res.add(cur.trim());
            // 注意: 别漏了return,否则死循环了
            return;
        }
        for (Integer j : dp[index]) {
            dfs(s, res, j, dp, s.substring(j, index) + " " + cur);
        }
    }
}

6. 最大子数组和

class Solution {
    // 1. 贪心
    public int maxSubArray(int[] nums) {
        int cur = 0;
        int max = Integer.MIN_VALUE;
        int n = nums.length;
        for (int i = 0; i < n; i++) {
            max = Math.max(cur + nums[i], max);
            if (nums[i] + cur > 0) {
                cur = cur + nums[i];
            } else {
                cur = 0;
            }
        }
        return max;
    }

    // 2. 动态规划
    public int maxSubArray(int[] nums) {
        int n = nums.length;
        // dp[i]:表示以i位置结束的最大子数组和
        int[] dp = new int[n];
        // 初始化
        dp[0] = nums[0];
        int max = dp[0];
        for (int i = 1; i < n; i++) {
            // 动态转移方程
            dp[i] = Math.max(nums[i], dp[i - 1] + nums[i]);
            max = Math.max(max, dp[i]);
        }
        return max;
    }
}

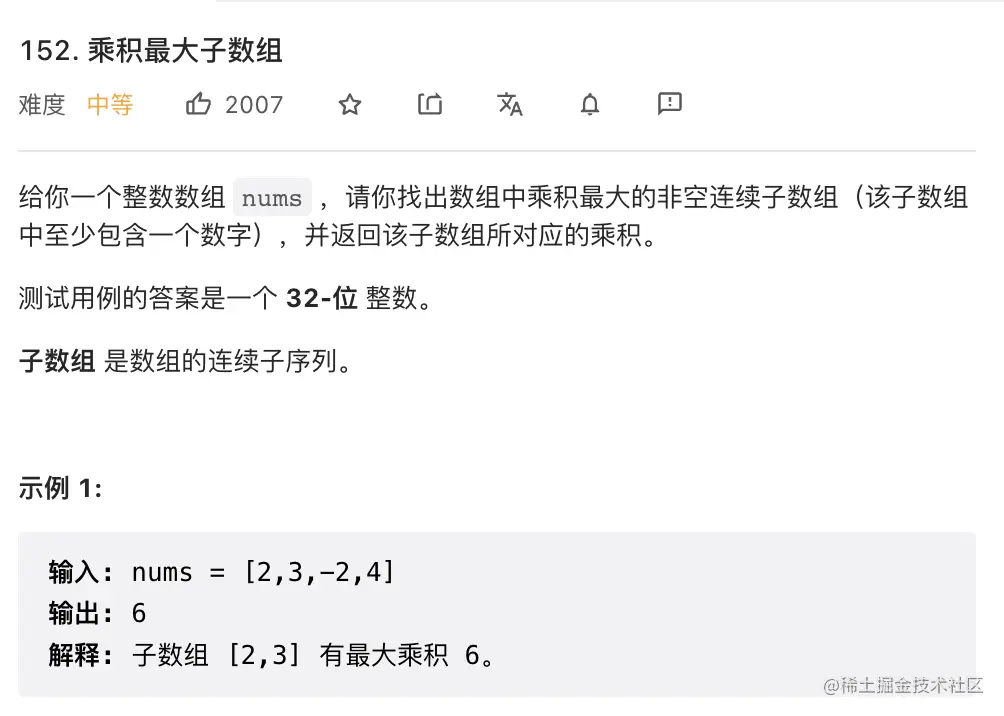
7. 乘积最大子数组

class Solution {
    public int maxProduct(int[] nums) {
        int n = nums.length;
        int[] min = new int[n];
        int[] max = new int[n];
        // 初始化
        min[0] = nums[0];
        max[0] = nums[0];
        int res = nums[0];
        for (int i = 1; i < n; i++) {
            if (nums[i] > 0) {
                max[i] = Math.max(nums[i], max[i - 1] * nums[i]);
                min[i] = Math.min(nums[i], min[i - 1] * nums[i]);
            } else {
                max[i] = Math.max(nums[i], min[i - 1] * nums[i]);
                min[i] = Math.min(nums[i], max[i - 1] * nums[i]);
            }
            res = Math.max(res, max[i]);
        }
        return res;
    }
}

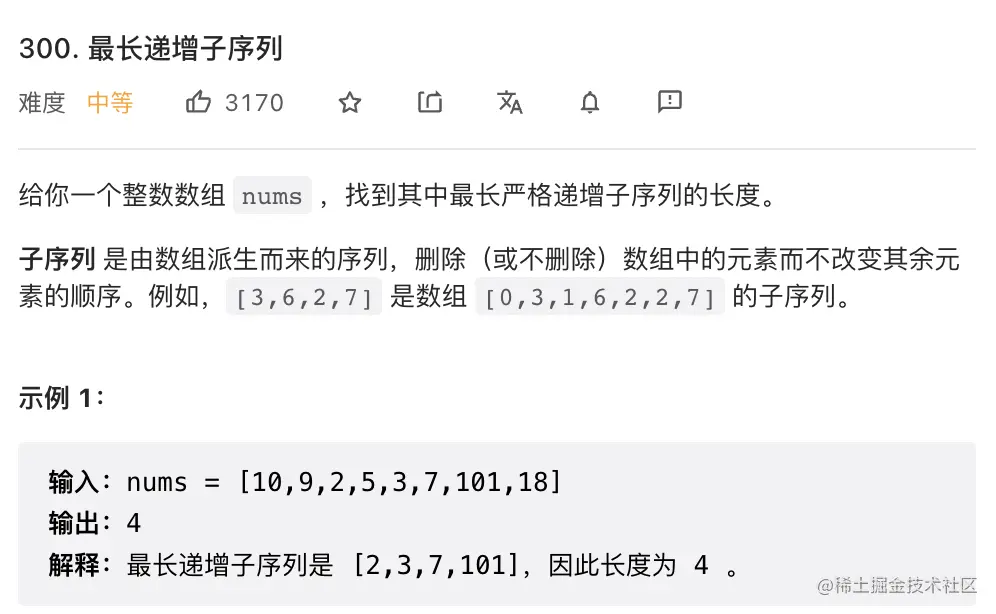
8. 最长递增子序列

class Solution {
    // 1. LIS问题:O(n^2)解法:通常面试官会让继续优化
    public int lengthOfLIS1(int[] nums) {
        int n = nums.length;
        // dp[i]:表示以i位置结尾的最长上升子序列长度
        int[] dp = new int[n];
        // 初始化
        Arrays.fill(dp, 1);
        int max = dp[0];
        for (int i = 1; i < n; i++) {
            for (int j = 0; j < i; j++) {
                if (nums[i] > nums[j]) {
                    dp[i] = Math.max(dp[i], dp[j] + 1);
                }
            }
            max = Math.max(max, dp[i]);
        }
        return max;
    }
}