哈希表是一种数据结构,以键值对的形式表示数据。每个键都映射到哈希表中的一个值。这些键用于索引值/数据。关联数组也采用了类似的方法。
数据通过键在键值对中表示,如下图所示。每个数据都与一个键相关联。键是一个指向数据的整数。
1.直接地址表
当程序使用的表空间量不是问题时,将使用直接地址表。在这里,我们假设
- 键是小整数
- 键的数量不是太大,并且
- 没有两个数据具有相同的密钥
取一个整数池,称为Universe U = {0, 1, ……., n-1} 。
直接地址表T[0...n-1]每个插槽都包含一个指向与数据相对应的元素的指针。
数组T的索引是键本身,而T的内容是指向集合[key, element]的指针。如果没有键的元素,则将其保留为NULL 。 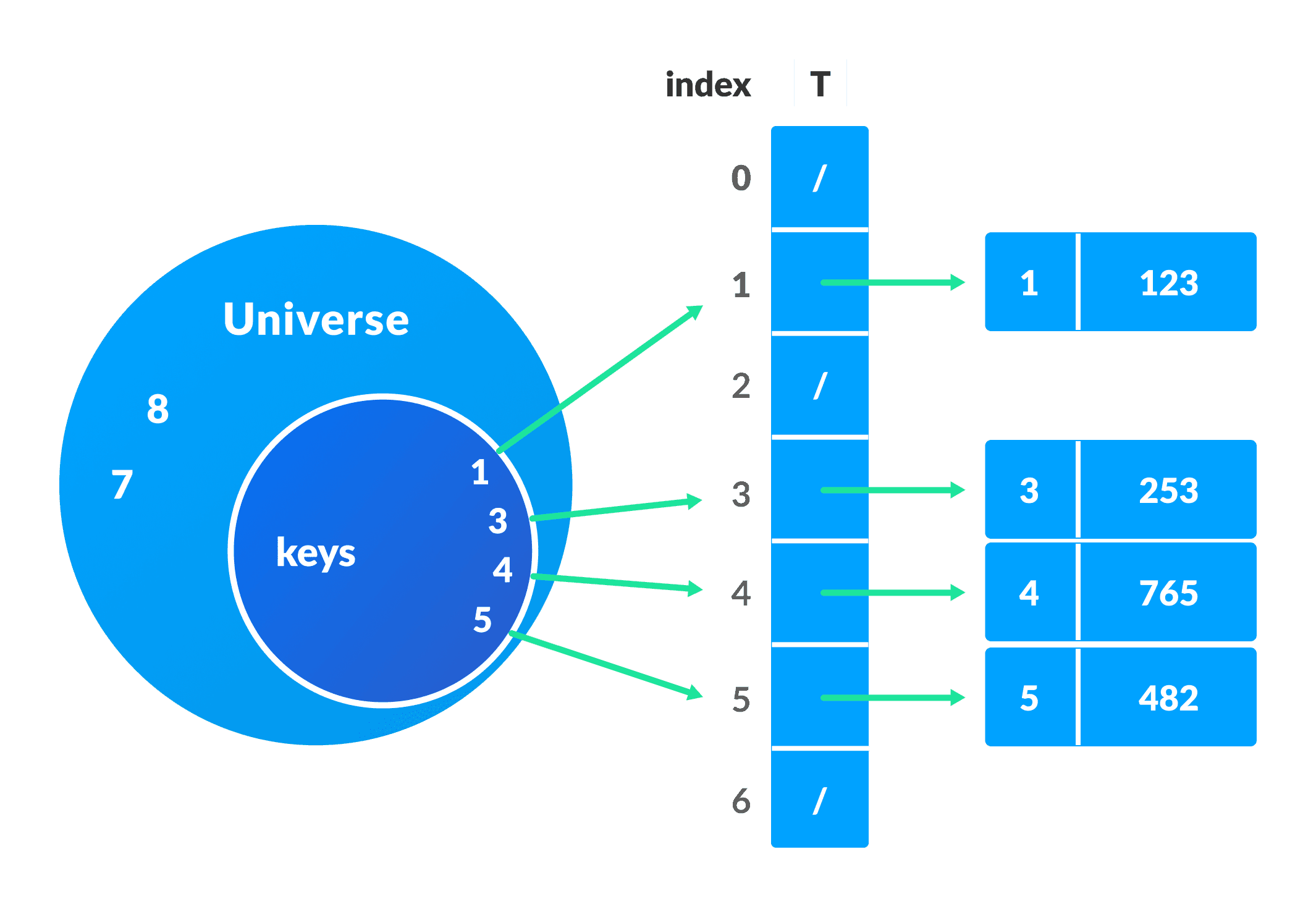
有时,关键本身就是数据。
伪代码用于操作
directAddressSearch(T, k)
return T[k]
directAddressInsert(T, x)
T[x.key] = x
directAddressDelete(T, x)
T[x.key] = NIL
直接地址表的局限性
- 密钥的值应该很小。
- 键的数量必须足够小,以使其不会超过数组的大小限制。
2.哈希表
在哈希表中,对键进行处理以产生映射到所需元素的新索引。此过程称为哈希。
令h(x)为哈希函数 , k为键。
计算h(k) ,并将其用作元素的索引。 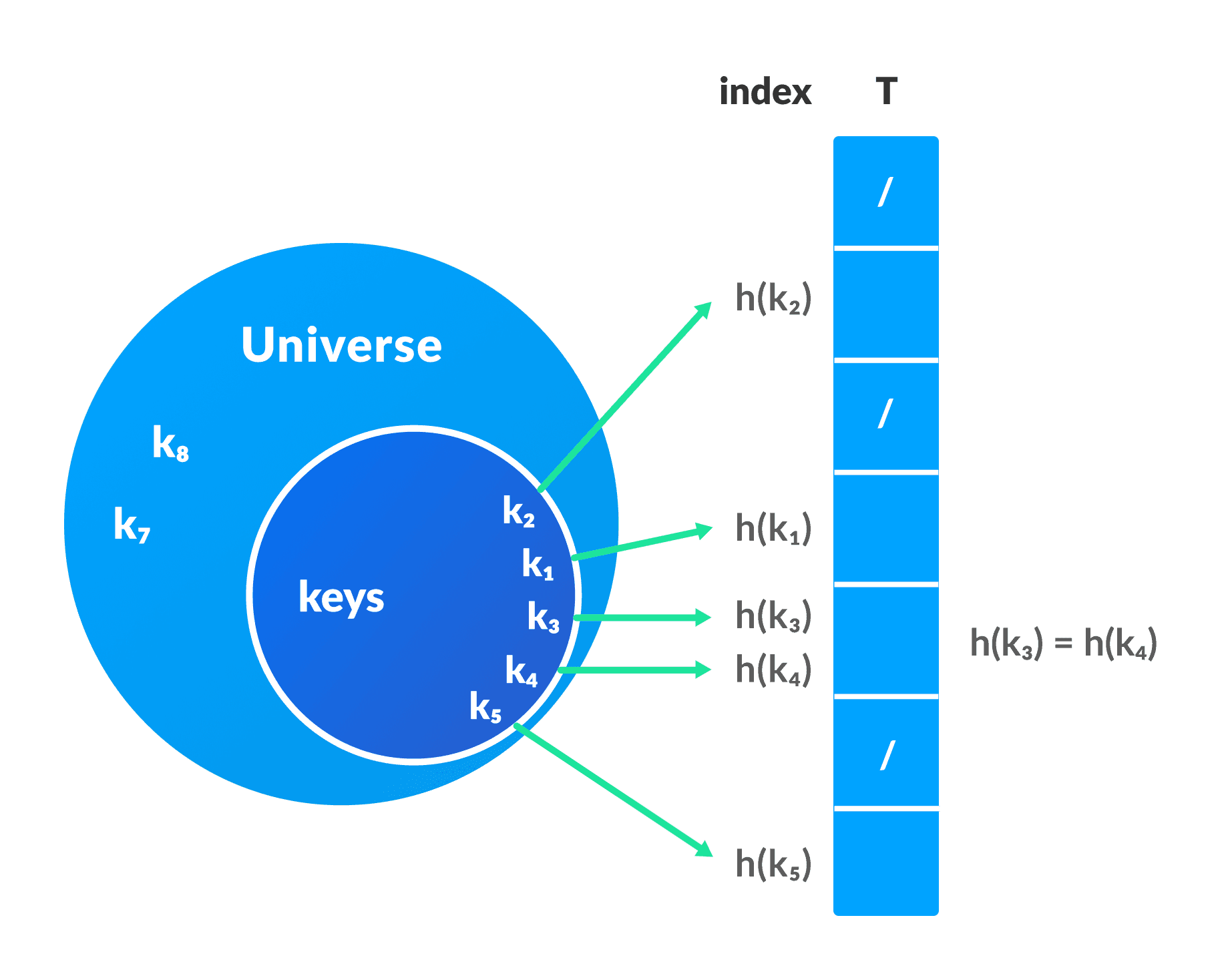
哈希表的局限性
- 如果散列函数为多个键产生相同的索引,则会产生冲突。这种情况称为碰撞。
为了避免这种情况,选择了合适的哈希函数 。但是,因为
|U|>m,所以不可能产生所有唯一的键。因此,良好的哈希函数可能无法完全防止冲突,但是可以减少冲突次数。
但是,我们还有其他解决冲突的技术。
哈希表优于直接地址表的优点:
直接地址表的主要问题是数组的大小和键的可能很大的值。哈希函数减小了索引的范围,因此数组的大小也减小了。
例如,如果k = 9845648451321 ,则h(k) = 11 (通过使用某些哈希函数)。这有助于节省浪费的内存,同时为阵列提供9845648451321的索引
链接解决冲突
在此技术中,如果哈希函数为多个元素生成相同的索引,则使用双向链表将这些元素存储在相同的索引中。
如果j是多个元素的插槽,则它包含一个指向元素列表头部的指针。如果不存在任何元素,则j包含NIL 。 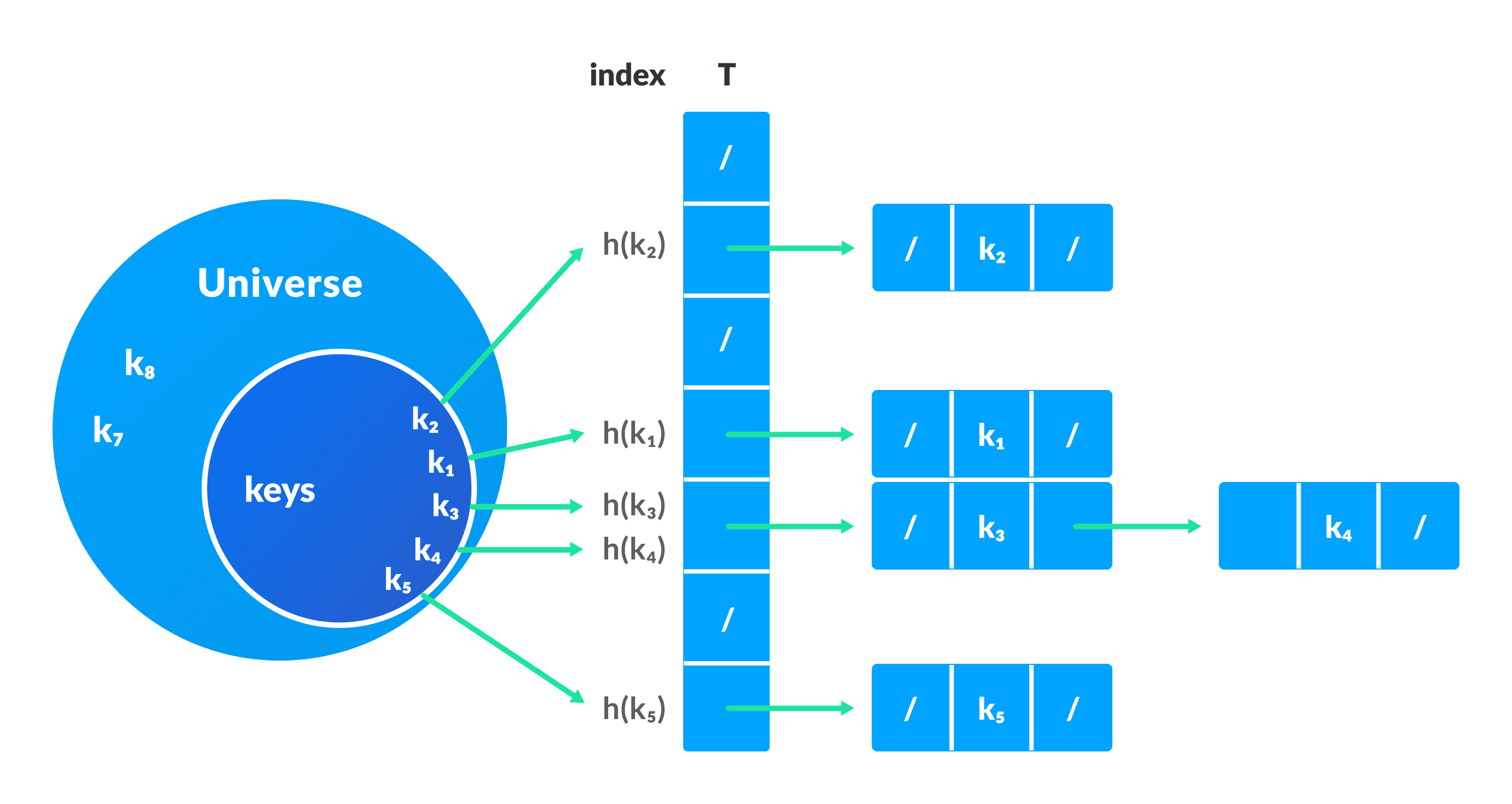
伪代码用于操作
chainedHashSearch(T, k)
return T[h(k)]
chainedHashInsert(T, x)
T[h(x.key)] = x //insert at the head
chainedHashDelete(T, x)
T[h(x.key)] = NIL
Python,Java,C和C++实现
# Python program to demonstrate working of HashTable
hashTable = [[],] * 10
def checkPrime(n):
if n == 1 or n == 0:
return 0
for i in range(2, n//2):
if n % i == 0:
return 0
return 1
def getPrime(n):
if n % 2 == 0:
n = n + 1
while not checkPrime(n):
n += 2
return n
def hashFunction(key):
capacity = getPrime(10)
return key % capacity
def insertData(key, data):
index = hashFunction(key)
hashTable[index] = [key, data]
def removeData(key):
index = hashFunction(key)
hashTable[index] = 0
insertData(123, "apple")
insertData(432, "mango")
insertData(213, "banana")
insertData(654, "guava")
print(hashTable)
removeData(123)
print(hashTable)
print(hashTable)
// Java program to demonstrate working of HashTable
import java.util.*;
class HashTable {
public static void main(String args[])
{
Hashtable
ht = new Hashtable();
ht.put(123, 432);
ht.put(12, 2345);
ht.put(15, 5643);
ht.put(3, 321);
ht.remove(12);
System.out.println(ht);
}
}
}
}
// Implementing hash table in C
#include <stdio.h>
#include <stdlib.h>
struct set
{
int key;
int data;
};
struct set *array;
int capacity = 10;
int size = 0;
int hashFunction(int key)
{
return (key % capacity);
}
int checkPrime(int n)
{
int i;
if (n == 1 || n == 0)
{
return 0;
}
for (i = 2; i < n / 2; i++)
{
if (n % i == 0)
{
return 0;
}
}
return 1;
}
int getPrime(int n)
{
if (n % 2 == 0)
{
n++;
}
while (!checkPrime(n))
{
n += 2;
}
return n;
}
void init_array()
{
capacity = getPrime(capacity);
array = (struct set *)malloc(capacity * sizeof(struct set));
for (int i = 0; i < capacity; i++)
{
array[i].key = 0;
array[i].data = 0;
}
}
void insert(int key, int data)
{
int index = hashFunction(key);
if (array[index].data == 0)
{
array[index].key = key;
array[index].data = data;
size++;
printf("\n Key (%d) has been inserted \n", key);
}
else if (array[index].key == key)
{
array[index].data = data;
}
else
{
printf("\n Collision occured \n");
}
}
void remove_element(int key)
{
int index = hashFunction(key);
if (array[index].data == 0)
{
printf("\n This key does not exist \n");
}
else
{
array[index].key = 0;
array[index].data = 0;
size--;
printf("\n Key (%d) has been removed \n", key);
}
}
void display()
{
int i;
for (i = 0; i < capacity; i++)
{
if (array[i].data == 0)
{
printf("\n array[%d]: / ", i);
}
else
{
printf("\n key: %d array[%d]: %d \t", array[i].key, i, array[i].data);
}
}
}
int size_of_hashtable()
{
return size;
}
int main()
{
int choice, key, data, n;
int c = 0;
init_array();
do
{
printf("1.Insert item in the Hash Table"
"\n2.Remove item from the Hash Table"
"\n3.Check the size of Hash Table"
"\n4.Display a Hash Table"
"\n\n Please enter your choice: ");
scanf("%d", &choice);
switch (choice)
{
case 1:
printf("Enter key -:\t");
scanf("%d", &key);
printf("Enter data -:\t");
scanf("%d", &data);
insert(key, data);
break;
case 2:
printf("Enter the key to delete-:");
scanf("%d", &key);
remove_element(key);
break;
case 3:
n = size_of_hashtable();
printf("Size of Hash Table is-:%d\n", n);
break;
case 4:
display();
break;
default:
printf("Invalid Input\n");
}
printf("\nDo you want to continue (press 1 for yes): ");
scanf("%d", &c);
} while (c == 1);
}</stdlib.h></stdio.h>} while (c == 1);
}</stdlib.h></stdio.h>
// Implementing hash table in C++
#include
#include
using namespace std;
class HashTable
{
int capacity;
list *table;
public:
HashTable(int V);
void insertItem(int key, int data);
void deleteItem(int key);
int checkPrime(int n)
{
int i;
if (n == 1 || n == 0)
{
return 0;
}
for (i = 2; i < n / 2; i++)
{
if (n % i == 0)
{
return 0;
}
}
return 1;
}
int getPrime(int n)
{
if (n % 2 == 0)
{
n++;
}
while (!checkPrime(n))
{
n += 2;
}
return n;
}
int hashFunction(int key)
{
return (key % capacity);
}
void displayHash();
};
HashTable::HashTable(int c)
{
int size = getPrime(c);
this->capacity = size;
table = new list[capacity];
}
void HashTable::insertItem(int key, int data)
{
int index = hashFunction(key);
table[index].push_back(data);
}
void HashTable::deleteItem(int key)
{
int index = hashFunction(key);
list::iterator i;
for (i = table[index].begin();
i != table[index].end(); i++)
{
if (*i == key)
break;
}
if (i != table[index].end())
table[index].erase(i);
}
void HashTable::displayHash()
{
for (int i = 0; i < capacity; i++)
{
cout << "table[" << i << "]";
for (auto x : table[i])
cout << " --> " << x;
cout << endl;
}
}
int main()
{
int key[] = {231, 321, 212, 321, 433, 262};
int data[] = {123, 432, 523, 43, 423, 111};
int size = sizeof(key) / sizeof(key[0]);
HashTable h(size);
for (int i = 0; i < n; i++)
h.insertItem(key[i], data[i]);
h.deleteItem(12);
h.displayHash();
}
h.deleteItem(12);
h.displayHash();
}
良好的哈希函数
良好的哈希函数具有以下特征。
- 它不应生成太大且存储桶空间小的密钥。空间被浪费了。
- 生成的密钥应该既不紧密也不在范围内。
- 必须尽可能减少碰撞。
用于散列的一些方法是:
除法
如果k是键,而m是哈希表的大小,则哈希函数 h()的计算公式为:
h(k) = k mod m
例如,如果哈希表的大小为10且k = 112则h(k) = 112 mod 10 = 2 。 m的值不得为2的幂。这是因为二进制格式的2的幂是10, 100, 1000, … 。当找到k mod m ,我们将始终获得较低阶的p位。
if m = 22, k = 17, then h(k) = 17 mod 22 = 10001 mod 100 = 01
if m = 23, k = 17, then h(k) = 17 mod 22 = 10001 mod 100 = 001
if m = 24, k = 17, then h(k) = 17 mod 22 = 10001 mod 100 = 0001
if m = 2p, then h(k) = p lower bits of m
乘法法
h(k) = ⌊m(kA mod 1)⌋
哪里,
-
kA mod 1给出小数部分kA, -
⌊ ⌋给出底值 -
A是任何常数。A的值介于0和1之间。但是,最佳选择将是Knuth建议的≈ (√5-1)/2。
通用哈希
在通用哈希中,哈希函数是独立于密钥随机选择的。
开放式寻址
多个值可以存储在普通哈希表的单个插槽中。
通过使用开放式寻址,每个插槽要么用单个键填充,要么用NIL左键填充。所有元素都存储在哈希表本身中。
与链接不同,多个元素无法放入同一插槽。
开放式寻址基本上是一种冲突解决技术。开放式寻址使用的一些方法是:
线性探测
在线性探测中,通过检查下一个插槽来解决冲突。
h(k, i) = (h′(k) + i) mod m
哪里,
-
i = {0, 1, ….} -
h'(k)是一个新的哈希函数
如果在h(k, 0)发生碰撞,则检查h(k, 1) 。这样, i的值线性增加。
线性探测的问题是相邻槽的簇被填充。插入新元素时,必须遍历整个集群。这增加了对哈希表执行操作所需的时间。
二次探测
在二次探测中,通过使用以下关系,可以增大槽之间的间距(大于1)。
h(k, i) = (h′(k) + c 1 i + c 2 i 2 ) mod m
哪里,
-
c 1和c 2是正辅助常数, -
i = {0, 1, ….}
双重哈希
如果在应用哈希函数 h(k)之后发生冲突,则将计算另一个哈希函数以查找下一个时隙。
h(k, i) = (h 1 (k) + ih 2 (k)) mod m
哈希表应用
哈希表在以下位置实现
- 需要持续的时间查找和插入
- 密码学应用
- 需要索引数据