活动安排

每场活动都要求使用同一资源, 且同一时间内只有一个活动能使用资源, 如果活动的活跃区间不相交, 则两个活动是 相容的

问题描述

$S=\{1,2,\cdots,n\}$ 为 $n$ 项活动, $s_i, f_i$ 分别为活动 $i$ 的开始时间和结束时间, 求最大的两两相容的活动集 $A$

时间复杂度(排序+活动选择):

O(nlogn)+O(n)=O(nlogn)

class Task:
    def __init__(self, s, f):
        self.id = None
        self.s = s
        self.f = f
        self.active = False


def select(s, f):
    n = len(s)

    tasks = []
    for i in range(n):
        tasks.append(Task(s[i], f[i]))

    tasks.sort(key=lambda x: x.f)

    for id, task in enumerate(tasks):
        task.id = id

    tasks[0].active = True

    count = 1
    j = 1

    for i in range(1, n):
        # 总是选择具有最早结束时间且相容的活动
        if tasks[i].s >= tasks[j].f:
            tasks[i].active = True
            j = i
            count += 1

    return count, [x.id + 1 for x in sorted(tasks, key=lambda x: x.id) if x.active]


s = [1, 3, 0, 5, 3, 5, 6, 8, 8, 2]  # 各活动开始时间
f = [4, 5, 6, 7, 8, 9, 10, 11, 12, 13]  # 各活动结束时间

# (4, [1, 4, 8, 11])
print(select(s, f))

正确性证明

算法 $select$ 执行到第 $k$ 步, 选择 $k$ 项活动 ( 活动按 $f_i$ 升序 ) , 那么最优解 $A$ 包含

<i_1=1, i_2 , \cdots , i_k>

意思是执行到第 k 步那么最优解肯定包含前 k 个活动, 符合贪心思想

当 $k=1$ 时, 令 $A$ 是一个最优解, 设 $k$ 是 $A$ 的 第一个 活动, 且令 $B=(A-\{k\}) \cup \{1\}$ , 由于 $f_1\le f_k$ , 因此选择更早结束的活动 $1$ 时各活动也是相容的, 且 $B$ 和 $A$ 活动数相同, $A$ 是最优的, 那么 $B$ 也是最优的, 且含有活动 $1$

执行到第 $k$ 步时, 有最优解 $A=\{1,i_2,\cdots, i_k\}$ , 令 $S=\{i|i\in S, s_i\ge f_k\}$ , 即剩余活动集合, 从中找到容量为 $C'=C-\sum_{i=1}^kw_i$ 的最优解 $B$ , 那么这个解必然包含活动 $k+1$ ( 即第一个活动, 若不包含, 做法同 $k=1$ ) , 也就是说, 第 $k+1$ 步时的解为

\{1,i_2,\cdots, i_k\}\cup\{i_{k+1}, \cdots\}=\{1,i_2,\cdots, i_k, i_{k+1}\}\cup\{\cdots\}

背包问题

0-1 背包 物品要么装入背包, 要么不装, 使装入的物品价值最大 ( 不能用贪心 )

但有一个特殊情况:

在 0-1 背包问题中, 若各物品依重量递增序排列时, 其价值恰好依递减序排列

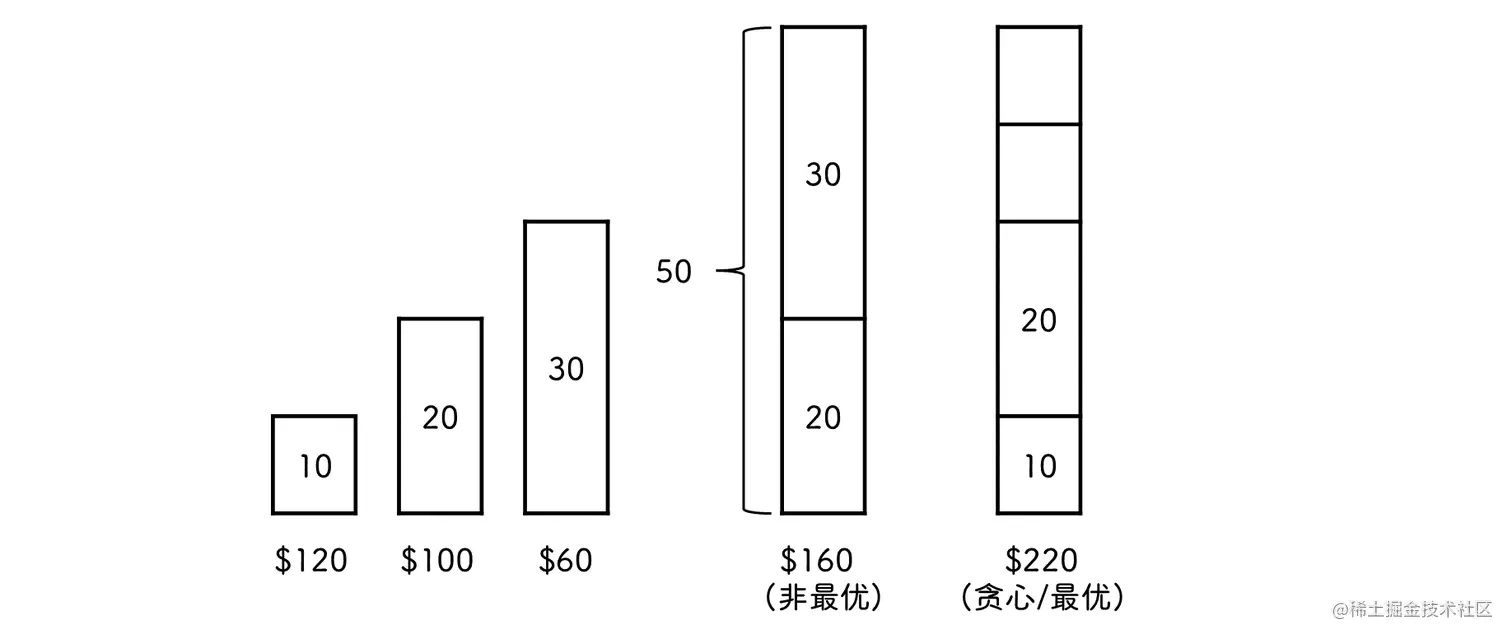
背包问题 物品可以选一部分装入背包(即不要求 100% 装入)

def knapsack(c, weights, v):
    w = enumerate(weights)

    # 根据单位重量价值降序, 每次选取单位重量价值最大的物品
    d = sorted(zip(w, v), key=lambda x: x[1] / x[0][1], reverse=True)

    opt = 0

    # 记录装入比例
    x = [0 for _ in range(len(weights))]

    for (i, w), v in d:
        if c >= w:
            # 能完全装入背包时
            opt += v
            c -= w
            x[i] = 1  # 代表装入 100%
        else:
            # 物品不能完全装入, 把部分装入填满背包
            opt += c * (v / w)
            x[i] = c / w
            break

    return opt, x

weights = [2, 2, 6, 5, 4]
values = [6, 3, 5, 4, 6]
capacity = 10

# (16.666666666666668, [1, 1, 0.3333333333333333, 0, 1])
print(knapsack(capacity, weights, values))

时间复杂度

O(nlogn)

最优装载

问题描述

一批集装箱要装到限重 $c$ 的轮船上, 体积不受限制, 要求尽可能多的集装箱装到轮船上

def loading(c, weights):
    # 根据重量升序
    d = sorted(enumerate(weights), key=lambda x: x[1])

    # 记录集装箱装入情况
    x = [0 for _ in range(len(weights))]

    opt = 0

    for i, w in d:
        if c >= w:
            # 总是选取质量较小的货物
            opt += w
            c -= w
            x[i] = 1
        else:
            break

    return opt, x


weights = [2, 2, 6, 5, 4]
capacity = 10

# (8, [1, 1, 0, 0, 1])
print(loading(capacity, weights))

正确性证明

对装载问题任何规模为 $k$ 的输入, “轻者优先”贪心法都可以得到最优解

$k=1$ 时, 只有一个货箱, 最优解为 $1$

问题规模为 $k+1$ 时, 集装箱集合为 $N=\{1,2,\cdots, k+1\}$ , 限重 $C$ , 令 $N'=\{2,3,\cdots,k+1\}$ 为规模为 $k$ 的装载问题, $C'=C-w_1$ , 假设命题成立, 则可以得到一个最优解 $I'$ , 原问题为 $N=N'\cup \{1\}$ , 令 $I=I'\cup \{1\}$ , 那么 $I$ 即为最优解

若存在一个更优解 $I^*$ 且包含箱子 $1$ (不包含则可以使用箱子 $1$ 替换 $I^*$ 中最轻的箱子), 那么箱子数 $|I^*| > |I|$ , $I^*-\{1\}$ 则为关于 $N'$ 的一个解, $|I^*-\{1\}|<|I-\{1\}|=I'$ , 与 $I'$ 为最优矛盾

哈夫曼编码

前缀码

用 0-1 字符串作为代码表示字符, 要求任何字符的代码都不能作为其它字符代码的前缀

平均位数

B=\sum_{i=1}^n f(x_i)d(x_i)

B=\frac{4 × (5 + 9) + 3 × (16 + 12 + 13) + 1 × 45}{100} = 2.24

最优前缀码

import heapq


class Node:
    def __init__(self, weight, id="", left=None, right=None):
        self.weight = weight
        self.left = left
        self.right = right
        self.id = id

    def __lt__(self, other):
        return self.weight < other.weight

    def __eq__(self, other):
        return self.weight == other.weight

    def __str__(self):
        return self.id


def huffman(freqs):
    nodes = [Node(v, id=k) for k, v in freqs.items()]

    heapq.heapify(nodes)  # 最小堆

    while len(nodes) > 1:
        # 获取两个最小编码长度的结点
        left = heapq.heappop(nodes)
        right = heapq.heappop(nodes)

        parent = Node(left.weight + right.weight, left=left, right=right)

        # 将合成的新节点重新放入堆中
        heapq.heappush(nodes, parent)

    return nodes[0]


# 前序遍历
def preorder(root):
    if root is None:
        return

    print(root.weight, root.id)
    preorder(root.left)
    preorder(root.right)


def main():
    freqs = {"a": 45, "b": 13, "c": 12, "d": 16, "e": 9, "f": 5}
    
    # 100 
    # 45 a
    # 55  
    # 25  
    # 12 c
    # 13 b
    # 30  
    # 14
    # 5 f
    # 9 e
    # 16 d
    preorder(huffman(freqs))


if __name__ == "__main__":
    main()

引理一

设 $C$ 是字符集, $\forall c \in C$ , $f(c)$ 为频率 , $x, y\in C$ , $f(x)$ 、 $f(y)$ 频率最小, 那么存在最优二元前缀码使得 $x, y$ 的码字等长, 且仅在最后一位不同

频率相同, 那么就会在树的同一深度, 那么编码长度也是一样的

引理二

设 $T$ 是二元前缀码所对应的二叉树， $\forall x, y\in T$ , $x$ , $y$ 是树叶兄弟, $z$ 是 $x$ , $y$ 的父亲, 令 $T' = T − \{x, y\}$ , 且令 $z$ 的频率 $f(z) = f(x)+f(y)$ , $T'$ 是对应于二元前缀码 $C' = (C−\{x, y\})\cup\{z\}$ 的二叉树, 那么 $B(T)=B(T')+f(x)+f(y)$

正确性证明

哈夫曼算法对 任意 规模为 $n (n ≥ 2)$ 的字符集 $C$ 都能得到关于 $C$ 的最优前缀码的二叉树

$n=2$ 时, 字符集 $C=\{x_1, x_2\}$ , 编码为 $0$ 和 $1$ , 是最优前缀码

对 $k+1$ 规模的字符集 $C=\{x_1, x_2, \cdots, x_{k+1}\}$ , 且 $x_1, x_2$ 是频率最小的两个字符, 令

C' = (C - \{x_1, x_2\})\cup\{z\}, f(z)=f(x)+f(y)

那么假设 $k$ 时命题成立, 则可得到一棵最优前缀码二叉树 $T'$

将 $T'$ 的 $z$ 节点替换成 $x_1, x_2$ , 得到的树 $T$ 即最优前缀码二叉树

假如存在一个更优的 $T^*$ , 即 $B(T^*) < B(T)$ , 它们都去掉 $x_1, x_2$ , 则

B(T^{*'}) = B(T^*)-f(x_1)-f(x_2) < B(T) - f(x_1)-f(x_2) = B(T')

这与 $B(T')$ 是最优的矛盾

单源最短路径

Dijkstra 算法

带权有向图 $G(V,E)$ , 设置一个顶点集合 $S$ , 一个顶点属于集合 $S$ 当且仅当从源到该点得最短路径已知

def dijkstra(graph, start):
    n = len(graph)

    dist = [float("inf") for _ in range(n)]
    visited = [False for _ in range(n)]
    path = [-1 for _ in range(n)]

    dist[start] = 0

    for i in range(n):
        min = float("inf")
        u = -1

        # 从未访问过的顶点中找出一条最短路径
        for j in range(n):
            if not visited[j] and dist[j] < min:
                min = dist[j]
                u = j

        # 没找到则说明已经到头了
        if u == -1:
            break

        visited[u] = True

        # 遍历与 u 邻接的所有顶点, 找到最短路径上 u 的下一个顶点
        for v in range(n):
            if graph[u][v] != 0 and not visited[v]:
                alt = dist[u] + graph[u][v]

                # 如果该点离起点的距离大于以 u 作为前驱时离起点的距离, 则更新最小距离
                if alt < dist[v]:
                    dist[v] = alt
                    path[v] = u

    return dist, path


# 邻接矩阵
graph = [
    [0, 10, 0, 0, 0, 3],
    [0, 0, 7, 5, 0, 0],
    [0, 0, 0, 0, 0, 0],
    [0, 0, 4, 0, 7, 0],
    [0, 0, 0, 0, 0, 0],
    [0, 2, 0, 6, 1, 0],
]


start = 0
dist, path = dijkstra(graph, start)

# dist: [0, 5, 12, 9, 4, 3]
print("dist:", dist)

# path: [-1, 5, 1, 5, 5, 0]
print("path:", path)


def get_path(path, end):
    res = [end]

    p = path[end]

    while p != -1:
        res.append(p)
        p = path[p]

    return res


# [2, 1, 5, 0]
print(get_path(path, 2))

正确性证明

说明为什么从 $s$ (源点)到 $u$ 最短路径一定是从 $s$ 到 $u$ 且仅经过 $S$ 中的顶点?

时间复杂度

O(n^2)

无法处理负权边

从 $A$ 出发最短路径 $A\rightarrow B$ , $B$ 标记访问, 继续从 $A$ 出发最短路径 $A\rightarrow C$ , 由于 $B$ 已经被访问, 因此 $C \rightarrow B$ 会被忽略, 然而其才是 $A\rightarrow B$ 的最短路径

最小生成树

无向连通带权图, 具有最小权的生成树

Prim 算法

原理: 每次都访问权最小的边

时间复杂度 $O(n^2)$

def find_min(graph, visit):
    min = float("inf")

    v1 = v2 = 0  # 最小权对应的点

    for i, row in enumerate(graph):
        if visit[i]:  # 从访问过的点中查找最小权边
            for j, col in enumerate(row):
                # 点未访问过且权重最小
                if not visit[j] and col != 0 and col < min:
                    min = col
                    v1 = i
                    v2 = j

    return v1, v2, min


def prim(graph):
    n = len(graph)  # 节点个数

    visit = [False for _ in range(n)]  # 记录访问过的点
    visit[0] = True

    res = [[0 for _ in range(n)] for _ in range(n)]

    for i in range(1, n):
        v1, v2, weight = find_min(graph, visit)
        visit[v2] = True
        res[v1][v2] = res[v2][v1] = weight

    return res


# 邻接矩阵
graph = [
    [0, 6, 1, 5, 0, 0],
    [6, 0, 5, 0, 3, 0],
    [1, 5, 0, 5, 6, 4],
    [5, 0, 5, 0, 0, 2],
    [0, 3, 6, 0, 0, 6],
    [0, 0, 4, 2, 6, 0],
]

# [0, 0, 1, 0, 0, 0]
# [0, 0, 5, 0, 3, 0]
# [1, 5, 0, 0, 0, 4]
# [0, 0, 0, 0, 0, 2]
# [0, 3, 0, 0, 0, 0]
# [0, 0, 4, 2, 0, 0]
for i in prim(graph):
    print(i)

正确性证明

$k=1$ , 存在一棵最小生成树包含 $e=(1,i)$ , 其中 $e$ 的权最小

假设 $T$ 是一棵最小生成树且不包含 $(1,i)$ , 那么 $T\cup(1,i)$ 必存在一条回路, 回路中与节点 $1$ 相连的边为 $(1,j)$ , 那么 $T'=(T-\{(1,j)\})\cup\{(1,i)\}$ 也是一棵生成树, 并且 $w(T') \le w(T)$ , $T'$ 是一棵最小的生成树

当执行到第 $k-1$ 步时, 最小生成树 $T_k$ 的边 $e_1, e_2, \cdots, e_{k-1}$ , 这些边的端点组成集合 $S$ , $T_k$ 中包含最小生成树的全部边

当执行到第 $k$ 步时, 选择了点 $i_{k+1}$ , $i_{k+1}$ 到已访问点集 $S$ 的权最小, 对应边 $e_k=(i_{k+1}, i_l)$ , 假设最小生成树不包含 $e_k$ , 那么将 $e_k$ 加入 $T$ 中并删除 $e_k'=(i_{k+1},i_l')$ , 那么 $T_{k+1}$ 是一棵最小生成树的边集

也就是说最小生成树的边集一定包含前 $k$ 个权最小边, 符合贪心原则

Kruskal 算法

原理: 将节点看作独立的连通分支, 边按权重排序, 依次查看, 若边连接的两个节点处于不同的连通分支, 则加入边, 若边连接的两个节点处于同一连通分支, 则跳过

时间复杂度: $O(mlogn)$

当边较多时, 如 $m=\Theta(n^2)$ , Kruskal 的复杂度为 $O(n^2logn)$ , 较 prim 差, 当边数较少时, 如 $m=\Theta(n)$ , Kruskal 的复杂度为 $O(nlogn)$ , 较 prim 优

class UnionFind:
    def __init__(self, n):
        self.parent = list(range(n))
        self.rank = [1] * n

    def find(self, x):
        if self.parent[x] != x:
            # 将路径上的节点的父节点都改成其祖先(根)
            self.parent[x] = self.find(self.parent[x])

        return self.parent[x]

    def union(self, x, y):
        px, py = self.find(x), self.find(y)

        # 祖先相同, 形成回路
        if px == py:
            return False

        # 秩大的做父节点
        if self.rank[px] < self.rank[py]:
            px, py = py, px

        self.parent[py] = px
        self.rank[px] += self.rank[py]

        return True


def kruskal(n, edges):
    uf = UnionFind(n)
    edges.sort(key=lambda x: x[2])  # 边按权重排序
    res = [[0 for _ in range(n)] for _ in range(n)]

    m = 0  # 已选边数

    for u, v, w in edges:
        # 树的边数等于点树减一, 此时已经生成一棵树了
        if m == n - 1:
            break

        if uf.union(u, v):
            m += 1
            res[u][v] = w
            res[v][u] = w

    return res


# 邻接矩阵
graph = [
    [0, 6, 1, 5, 0, 0],
    [6, 0, 5, 0, 3, 0],
    [1, 5, 0, 5, 6, 4],
    [5, 0, 5, 0, 0, 2],
    [0, 3, 6, 0, 0, 6],
    [0, 0, 4, 2, 6, 0],
]

n = len(graph)
edges = []

for i in range(n):
    for j in range(i + 1, n):
        if graph[i][j] != 0:
            edges.append((i, j, graph[i][j]))

# [0, 0, 1, 0, 0, 0]
# [0, 0, 5, 0, 3, 0]
# [1, 5, 0, 0, 0, 4]
# [0, 0, 0, 0, 0, 2]
# [0, 3, 0, 0, 0, 0]
# [0, 0, 4, 2, 0, 0]
for i in kruskal(n, edges):
    print(i)

正确性证明

$n=2$ 时, 只有一条边, 命题成立

当 $n+1$ 个顶点构成图 $G$ 时, 存在最小权边 $e=(i,j)$ , 将 $i$ 和 $j$ 短接, 得到图 $G'$ , 若命题成立, 那么能得到一棵最小生成树 $T'$ , 令 $T=T'\cup\{e\}$ , 那么 $T$ 是 $G$ 的最小生成树

若不是, 说明存在一棵更小的生成树 $T^*$ 使得 $w(T^*) < w(T)$ , $w(T^*-\{e\})=w(T^*)-w(e)<w(T-\{e\})=w(T')$ , 与 $T'$ 是最小生成树相互矛盾

调度问题

多机调度

m 台机器, n 个作业, 每个作业处理时间 $t_i$ , 要求在尽可能短的时间内完成全部作业

思路: 最长处理时间优先

def job(m, t):
    n = len(t)

    if n <= m:
        # 机器数多于作业数, 为每个作业分配机器
        # 完成时间为最大作业时间
        return max(t)

    # 处理时间从大到小排序
    times = sorted(enumerate(t), key=lambda x: x[1], reverse=True)

    consumes = [0 for _ in range(m)]  # 记录每个机器的耗时
    machines = [[] for _ in range(m)]  # 记录机器的分配情况

    for i, t in times:
        # 找到总时间消耗最小的机器
        min_cons = min(consumes)
        idx = consumes.index(min_cons)

        # 将当前作业分配给该机器
        consumes[idx] += t
        machines[idx].append(i + 1)

    return max(consumes), machines


def main():
    times = [2, 14, 4, 16, 6, 5, 3]
    job_num = 3

    # (17, [[4], [2, 7], [5, 6, 3, 1]])
    print(job(job_num, times))


if __name__ == "__main__":
    main()

最小延迟调度

给定客户集合 A， $\forall i \in A$ , $t_i$ 为服务时间, $d_i$ 为完成时间, $t_i$ , $d_i$ 为正整数, 一个调度是函数 $f: A \rightarrow N$ , $f(i)$ 为客户 i 的开始时间, 求最大延迟达到最小的调度

意思是即使不能按时结束服务, 也要尽量使这个延迟减小

\underset{f}{min}\ {\underset{i\in A}{max}\ \{f(i) + t_i - d_i\}}

其中 $\underset{i\in A}{max}\ \{f(i) + t_i - d_i\}$ 指最大延迟

如上图所示, 服务 2 的服务时长为 8, 结束时间为 12, 对于调度 1 来说, 晚结束了 1, 对于调度 2 来说, 晚结束了 15

思路: 按完成时间从早到晚安排任务

def schedule(T, D):
    n = len(D)
    d = sorted(enumerate(D), key=lambda x: x[1])  # 完成时间升序

    f = [0 for _ in range(n)]  # 记录各任务开始时间
    late = [0 for _ in range(n)]  # 记录各任务延时

    pre = d[0][0]  # 第一个任务编号
    s = [pre + 1]  # 记录第一个任务
    
    # 记录第一个任务延时
    late[0] = 0 if T[pre] <= D[pre] else T[pre] - D[pre]

    for id, item in d[1:]:
        # 计算当前任务开始时间
        f[id] = f[pre] + T[pre]
        
        # 当前任务结束时间比预期结束时间多多长时间
        dT = f[id] + T[id] - item
        
        # 如果超时则记录超时时间
        if dT > 0:
            late[id] = dT
        
        # 插入当前作业
        s.append(id + 1)
        pre = id

    return {
        "max_late": max(late),
        "late": late,
        "schedule": s,
        "start_time": f,
    }


def main():
    T = [5, 8, 4, 10, 3]
    D = [10, 12, 15, 11, 20]

    # {
    #   "max_late": 12,
    #   "late": [0, 11, 12, 4, 10],
    #   "schedule": [1, 4, 2, 3, 5],
    #   "start_time": [0, 15, 23, 5, 27],
    # }
    print(schedule(T, D))


if __name__ == "__main__":
    main()

引理一

所有没有逆序、没有空闲时间的调度具有相同的最大延迟

逆序指 $f(i) < f(j)$ 且 $d_i > d_j$ , 即开始的早, 预计结束的又晚

具有相同结束时间 $d$ ( 即没有逆序 )的活动必被连续安排, 那么这些活动中最大延迟必是最后一个被安排的活动

t_0+\sum_{i=0}^kt_i-d

因此这些活动的调度(排序)方式不会影响最大延迟, 因此解是等价的

定理一

在一个没有空闲时间的最优解中, 最大延迟是 $r$ , 如果仅对具有相邻逆序的客户进行交换, 得到的解的最大延迟不会超过 $r$

交换相邻逆序 (i, j) 不影响最优性

交换 $i, j$ 对其他客户的延迟时间没影响

由于 $d_i > d_j$ ( 逆序性质 ), 根据

delay(f, j) = s + t_i + t_j - d_j

delay(f', i) = s + t_j + t_i - d_i

因此

delay(f', i) < delay(f, j)

不会超过原来的延迟, 因此不断交换两个相邻逆序( 实际上是将结束时间早的活动提前 )不会导致最大延迟增加, 符合贪心原则

贪心与最优解判断条件(不考)

定理一

对每个正整数 $k$ , 假设对所有非负整数 $y$ 有 $G_k(y) = F_k(y)$ , 那么

G_{k+1}(y) \le G_k(y) \longleftrightarrow F_{k+1}(y) = G_{k+1}(y)

$G_k(y)$ 指贪心算法的解, $F_k(y)$ 指动态规划的解

定理二

对每个正整数 $k$ , 假设对所有非负整数 $y$ 有 $G_k(y) = F_k(y)$ , 且存在 $p$ 和 $δ$ 满足 $v_{k+1} = pv_k − \delta$ , 其中 $0 \lt \delta < v_k$ , $v_k < v_{k+1}$ , $p$ 为正整数, 则下列命题等价

G\_{k+1}(y) = F\_{k+1}(y)

G\_{k+1}(pv\_k) = F\_{k+1}(pv\_k)

w\_{k+1} + G\_k(\delta) \le pw\_k

$v_1 = 1$ , $v_2 = 5$ , $v_3 = 14$ , $v_4 = 18$ , $w_i = 1$ , $i = 1, 2, 3, 4$

对一切 $y$ 有 $G_1(y)=F_1(y)$ , $G_2(y)=F_2(y)$ , 验证 $G_3(y) = F_3(y)$

取 $p = 3$ , $\delta = 1$ , 有 $v_3 = pv_2 - \delta$

$w_3 + G_2(\delta) = 1 + 1 = 2$

$pw_2 = 3 × 1 = 3$

根据 $w_3 + G_2(\delta) \le pw_2$ 可得 $G_3(y) = F_3(y)$