• 只有有向无环图才有拓扑序
• 时间复杂度O(n + m)，n表示点数，m表示边数

模板

• C++

bool topsort()
{
    int hh = 0, tt = -1;

    // d[i] 存储点i的入度
    for (int i = 1; i <= n; i ++ )
        if (!d[i])
            q[ ++ tt] = i;

    while (hh <= tt)
    {
        int t = q[hh ++ ];

        for (int i = h[t]; i != -1; i = ne[i])
        {
            int j = e[i];
            if (-- d[j] == 0)
                q[ ++ tt] = j;
        }
    }

    // 如果所有点都入队了，说明存在拓扑序列；否则不存在拓扑序列。
    return tt == n - 1;
}

• Java

public static int[] d = new int[N];  //d[i]存储i的入度
public static int[] q = new int[N];  //队列

public static boolean top_sort() {
    int hh = 0, tt = -1;
    
    for (int i = 1; i <= n; i++) {
        if (d[i] == 0) {
            q[++tt] = i;
        }
    }
    
    while (hh <= tt) {
        int t = q[hh++];
        
        for (int i = h[t]; i != -1; i = ne[i]) {
            int j = e[i];
            if (--d[j] == 0) {
                q[++tt] = j;
            }
        }
    }
    
    // 如果所有点都入队了，说明存在拓扑序列；否则不存在拓扑序列
    return tt == n - 1;
}

练习

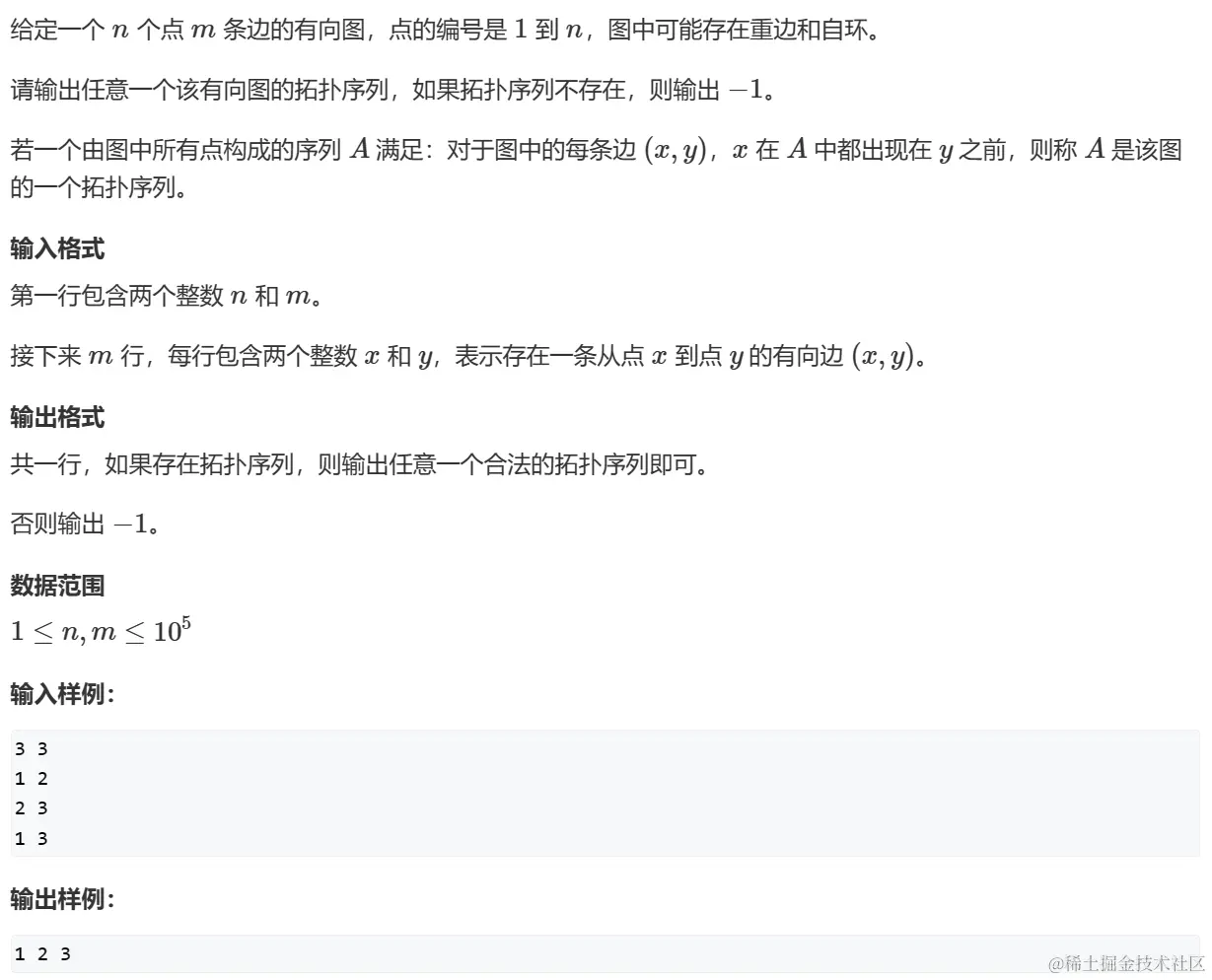
01 有向图的拓扑序列

• 题目

• 题解

import java.io.*;
import java.util.*;

public class Main {
    public static final int N = 100010;
    public static final int M = N * 2;
    public static int[] h = new int[N];
    public static int[] e = new int[M];
    public static int[] ne = new int[M];
    public static int[] d = new int[N];
    public static int[] q = new int[N];
    public static int n, m, idx;

    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        PrintWriter pw = new PrintWriter(new OutputStreamWriter(System.out));
        String[] str1 = br.readLine().split(" ");
        n = Integer.parseInt(str1[0]);
        m = Integer.parseInt(str1[1]);
        idx = 0;
        Arrays.fill(h, -1);
        while (m-- > 0) {
            String[] str2 = br.readLine().split(" ");
            int a = Integer.parseInt(str2[0]);
            int b = Integer.parseInt(str2[1]);
            add(a, b);
        }

        if (top_sort()) {
            //先进队的更小
            for (int i = 0; i < n; i++) {
                pw.print(q[i] + " ");
            }
        } else {
            pw.println(-1);
        }
        br.close();
        pw.close();
    }

    public static void add(int a, int b) {
        e[idx] = b;
        ne[idx] = h[a];
        h[a] = idx++;
        d[b]++;
    }

    public static boolean top_sort() {
        //tt为队尾 hh为队头
        int tt = -1, hh = 0;

        //遍历每一个点，如果该点的入度为0，添加进队
        for (int i = 1; i <= n; i++) {
            if (d[i] == 0) {
                q[++tt] = i;
            }
        }

        while (hh <= tt) {
            //每次获取队头元素
            int t = q[hh++];

            for (int i = h[t]; i != -1; i = ne[i]) {
                int j = e[i];
                //删去 i -> j 的有向边后如果入度为0
                if (--d[j] == 0) {
                    //添加进队
                    q[++tt] = j;
                }
            }
        }
        //如果所有点都添加进队了，说明存在拓扑排序
        return tt == n - 1;
    }
}