-
491递增子序列
- 代码随想录 (programmercarl.com)
-
第一印象
- 因为是要找到数组的递增子序列,所以就不能进行排序了。本题的难点在于如何去重。
-
讲解观后感
- 首先还是要确认本题的去重方式是同层去重而不是同枝去重。然后可以利用map里记录本层已经使用过的元素。
-
解题代码
-
func findSubsequences(nums []int) [][]int {
ans := make([][]int, 0)
if len(nums) <2 {
return ans
}
path := make([]int, 0, len(nums))
var backtrac func(nums []int, idx int)
backtrac = func(nums []int, idx int) {
if len(path)>1 {
tmp := make([]int, len(path))
copy(tmp, path)
ans = append(ans, tmp)
}
used := make(map[int]bool, len(nums))
for i:=idx;i<len(nums);i++ {
if used[nums[i]] {
continue
}
if len(path)==0 || nums[i]>=path[len(path)-1] {
path = append(path, nums[i])
used[nums[i]] = true
backtrac(nums, i+1)
path = path[:len(path)-1]
}
}
}
backtrac(nums, 0)
return ans
}
-
46全排列
- 代码随想录 (programmercarl.com)
-
第一印象
- 排列问题和组合问题的变化,一个是同层的下一次搜索可以从头开始查找,因为不会出现重复数字,所以不需要考虑去重。但是需要记录同树枝使用过的元素,可以使用map记录使用情况,在回溯函数中传参。
-
解题代码
- 使用map记录
-
func permute(nums []int) [][]int {
ans := make([][]int, 0)
path := make([]int, 0, len(nums))
used := make(map[int]bool, len(nums))
var backtrac func(nums []int, used map[int]bool)
backtrac = func(nums []int, used map[int]bool) {
if len(path)==len(nums) {
tmp := make([]int, len(path))
copy(tmp, path)
ans = append(ans, tmp)
return
}
for i:=0;i<len(nums);i++ {
if !used[nums[i]] {
path = append(path, nums[i])
used[nums[i]] = true
backtrac(nums, used)
used[nums[i]] = false
path = path[:len(path)-1]
}
}
}
backtrac(nums, used)
return ans
}
- 使用数组记录
-
var (
res [][]int
path []int
st []bool
)
func permute(nums []int) [][]int {
res, path = make([][]int, 0), make([]int, 0, len(nums))
st = make([]bool, len(nums))
dfs(nums, 0)
return res
}
func dfs(nums []int, cur int) {
if cur == len(nums) {
tmp := make([]int, len(path))
copy(tmp, path)
res = append(res, tmp)
}
for i := 0; i < len(nums); i++ {
if !st[i] {
path = append(path, nums[i])
st[i] = true
dfs(nums, cur + 1)
st[i] = false
path = path[:len(path)-1]
}
}
}
-
47全排列II
- 代码随想录 (programmercarl.com)
-
第一印象
- 在基础的全排列中怎增加了重复的元素,于是就要想办法也在同层之中去重。也许可以多用一个used数组再来记录同层的使用情况。
-
讲解观后感
- 多使用一个used数组的方式是不对的,因为同枝不同层的去重逻辑是只要不重复使用同一个位置的数字。而同层的逻辑是不能使用同样大小的数字。而且在同层内也不能使用mao存储的方式去重,因为每次遍历都是从开头重来的,所以第一次出现的数字会造成后面所有的数字无法获取。
- 所以我们还是使用排序后查看前一个数字的方式。这样能够获取重复的数字。
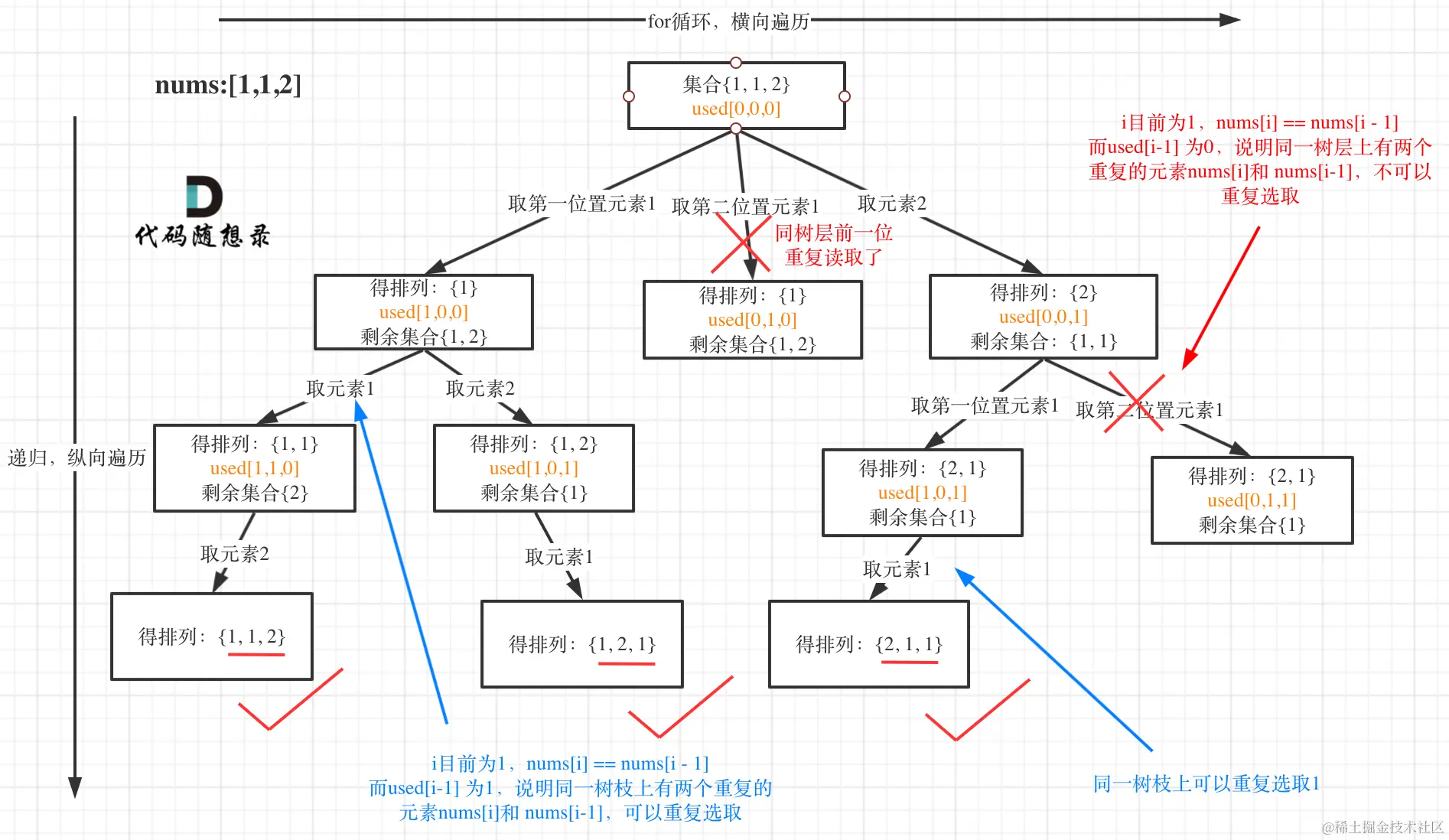
- 同树层去重逻辑的示意图:
-
出现问题