• 将两个集合合并
• 询问两个元素是否在一个集合当中
• 并查集可以在近乎O(1)的时间内完成这两个操作
• 基本原理：每个集合用一棵树来表示，树根的编号就是整个集合的编号，每个节点存储它的父节点，p[x]表示x的父节点
• 如何判断树根？
  • if (p[x] == x)
• 如何求x的集合编号？
  • while (p[x] != x) {x = p[x]};
• 如何合并两个集合？
  • px是x的集合编号，py是y的集合编号，p[x] = y
• 优化：路径压缩
  • 查找时将路径上的每一个节点都指向树根

模板

朴素并查集

• C++

int p[N]; //存储每个点的祖宗节点

    // 返回x的祖宗节点 + 路径压缩
    int find(int x)
    {
        if (p[x] != x) p[x] = find(p[x]);
        return p[x];
    }

    // 初始化，假定节点编号是1~n
    for (int i = 1; i <= n; i ++ ) p[i] = i;

    // 合并a和b所在的两个集合：
    p[find(a)] = find(b);

维护size的并查集

• C++

int p[N], size[N];
    //p[]存储每个点的祖宗节点, size[]只有祖宗节点的有意义，表示祖宗节点所在集合中的点的数量

    // 返回x的祖宗节点
    int find(int x)
    {
        if (p[x] != x) p[x] = find(p[x]);
        return p[x];
    }

    // 初始化，假定节点编号是1~n
    for (int i = 1; i <= n; i ++ )
    {
        p[i] = i;
        size[i] = 1;
    }

    // 合并a和b所在的两个集合：
    size[find(b)] += size[find(a)];
    p[find(a)] = find(b);

维护到祖宗节点距离的并查集

• C++

    int p[N], d[N];
    //p[]存储每个点的祖宗节点, d[x]存储x到p[x]的距离

    // 返回x的祖宗节点
    int find(int x)
    {
        if (p[x] != x)
        {
            int u = find(p[x]);
            d[x] += d[p[x]];
            p[x] = u;
        }
        return p[x];
    }

    // 初始化，假定节点编号是1~n
    for (int i = 1; i <= n; i ++ )
    {
        p[i] = i;
        d[i] = 0;
    }

    // 合并a和b所在的两个集合：
    p[find(a)] = find(b);
    d[find(a)] = distance; // 根据具体问题，初始化find(a)的偏移量

练习

01 集合合并

• 题目

• 题解

import java.io.*;

public class Main {
    public static final int N = 100010;
    public static int[] p = new int[N];
    public static int n, m;

    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        PrintWriter pw = new PrintWriter(new BufferedWriter(new OutputStreamWriter(System.out)));
        String[] str1 = br.readLine().split(" ");
        n = Integer.parseInt(str1[0]);
        m = Integer.parseInt(str1[1]);
        for (int i = 1; i <= n; i++) {
            p[i] = i;
        }

        while (m-- > 0) {
            String[] str2 = br.readLine().split(" ");
            if (str2[0].equals("M")) {
                p[find(Integer.parseInt(str2[1]))] = find(Integer.parseInt(str2[2]));
            } else {
                if (find(Integer.parseInt(str2[1])) == find(Integer.parseInt(str2[2]))) {
                    pw.println("Yes");
                } else {
                    pw.println("No");
                }
            }
        }
        pw.close();
        br.close();
    }

    public static int find(int x) {
        if (p[x] != x) {
            p[x] = find(p[x]);
        }
        return p[x];
    }
}

02 连通块中点的数量

• 题目

• 题解

import java.io.*;

public class Main {
    public static final int N = 100010;
    public static int[] p = new int[N];
    public static int size[] = new int[N];
    public static int n, m;

    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        PrintWriter pw = new PrintWriter(new BufferedWriter(new OutputStreamWriter(System.out)));
        String[] str1 = br.readLine().split(" ");
        n = Integer.parseInt(str1[0]);
        m = Integer.parseInt(str1[1]);
        for (int i = 1; i <= n; i++) {
            p[i] = i;
            size[i] = 1;
        }

        while (m-- > 0) {
            String[] str2 = br.readLine().split(" ");
            if (str2[0].equals("C")) {
                int a = Integer.parseInt(str2[1]);
                int b = Integer.parseInt(str2[2]);
                if (find(a) != find(b)) {
                    size[find(b)] += size[find(a)];
                    p[find(a)] = find(b);
                }
            } else if (str2[0].equals("Q1")) {
                int a = Integer.parseInt(str2[1]);
                int b = Integer.parseInt(str2[2]);
                if (find(a) == find(b)) {
                    pw.println("Yes");
                } else {
                    pw.println("No");
                }
            } else {
                int a = Integer.parseInt(str2[1]);
                pw.println(size[find(a)]);
            }
        }
        pw.close();
        br.close();
    }

    public static int find(int x) {
        if (p[x] != x) {
            p[x] = find(p[x]);
        }
        return p[x];
    }
}

03 食物链

• 题目

• 题解

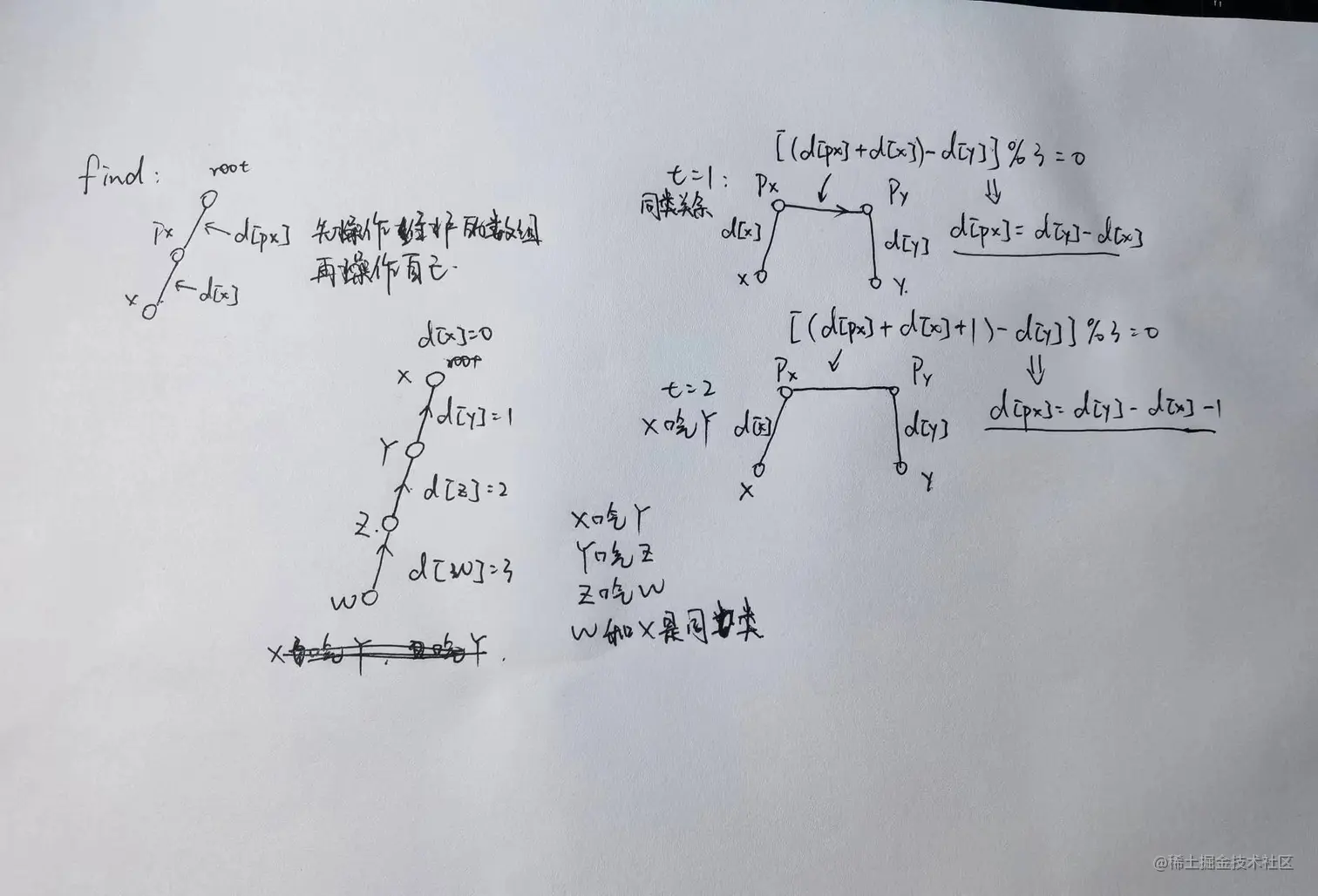
import java.io.*;

public class Main {
    public static final int N = 50010;
    //存储每个动物的父节点
    public static int[] p = new int[N];
    //x到p[x]的距离
    public static int[] d = new int[N];
    public static int n, k;

    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        PrintWriter pw = new PrintWriter(new BufferedWriter(new OutputStreamWriter(System.out)));
        String[] str1 = br.readLine().split(" ");
        n = Integer.parseInt(str1[0]);
        k = Integer.parseInt(str1[1]);
        for (int i = 1; i <= n; i++) {
            p[i] = i;
            d[i] = 0;
        }
        int res = 0;

        while (k-- > 0) {
            String[] str2 = br.readLine().split(" ");
            int t = Integer.parseInt(str2[0]);
            int x = Integer.parseInt(str2[1]);
            int y = Integer.parseInt(str2[2]);
            if (x > n || y > n) {
                res++;
            } else {
                int px = find(x);
                int py = find(y);
                if (t == 1) {
                    //如果在同一棵树里，直接验证是否正确
                    if (px == py && (d[y] - d[x]) % 3 != 0) {
                        res++;
                    } else if (px != py) {  //如果不在同一棵树内，则作为已知条件存入树中
                        //看图解
                        p[px] = p[y];
                        d[px] = d[y] - d[x];
                    }
                } else {
                    //如果在同一棵树里，直接验证是否正确
                    if (px == py && (d[y] - d[x] - 1) % 3 != 0) {
                        res++;
                    } else if (px != py) {  //如果不在同一棵树内，则作为已知条件存入树中
                        //看图解
                        p[px] = p[y];
                        d[px] = d[y] - d[x] - 1;
                    }
                }
            }
        }
        pw.println(res);
        pw.close();
        br.close();
    }

    public static int find(int x) {
        if (p[x] != x) {
            int t = find(p[x]);
            d[x] += d[p[x]];
            p[x] = t;
        }
        return p[x];
    }
}