transformation

Douglas_o
50 阅读9分钟

[[toc]]

1.线性变换

缩放和旋转都能以线性变换的形式来表示，即：

x1=ax0+by0y1=cx0+dy0x_1 = ax_0 + by_0 \\ y_1 = cx_0 + dy_0

以矩阵的形式来表示即：

[x1y1]=[ABCD][x0y0]\begin{bmatrix} x_1 \\ y_1 \end{bmatrix} = \begin{bmatrix} A & B \\ C & D \end{bmatrix} \begin{bmatrix} x_0 \\ y_0 \end{bmatrix}

如果变换可以通过以矩阵M 与点相乘然后得到一个新的点的话，那么这种变换就可以称为是线性变换

下面为常见的线性变换：缩放变换及旋转变换

[1]缩放

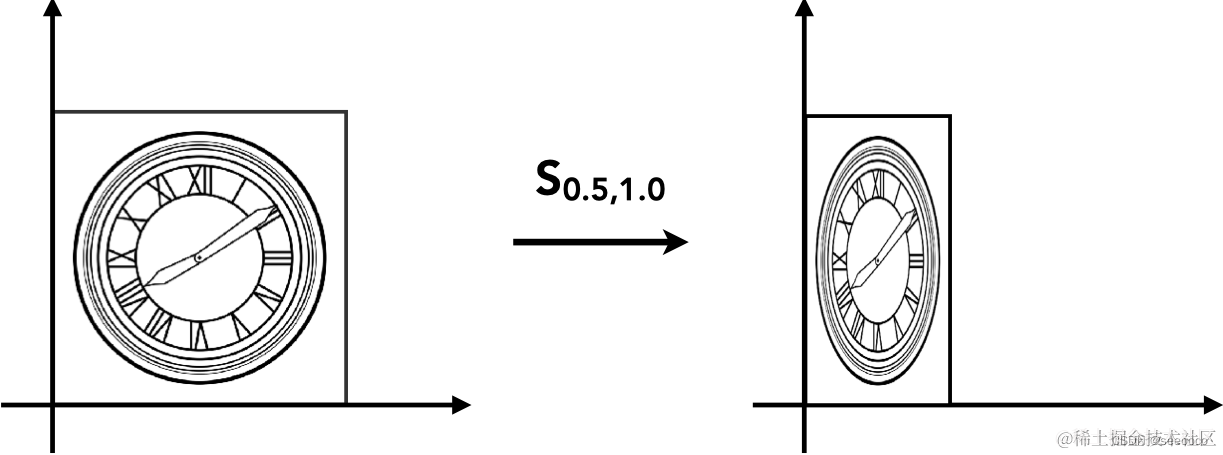
在这里插入图片描述

缩放是指点 (x0,y0)(x_0,y_0) 经过缩放因子 S(x,y)S(x,y) 变换之后形成新的点(x1,y1) (x_1,y_1)，它们间的关系是：

x1=Sx×x0y1=Sy×Y0x_1 = S_x \times x_0 \\ y_1 = S_y \times Y_0

写成矩阵的形式：

[x1y1]=[SX00Sy][x0y0]\begin{bmatrix} x_1 \\ y_1 \\ \end{bmatrix} = \begin{bmatrix} S_X & 0 \\ 0 & S_y \\ \end{bmatrix} \begin{bmatrix} x_0 \\ y_0 \\ \end{bmatrix}

镜像是一个非常常见的缩放变换，只需要把缩放因子变成负数即可实现某个方向的镜像。如当缩放因子是 (−1,1)(−1,1) 时，经过缩放变换之后的图形就是以 Y 轴为对称轴的镜像。

[2]旋转

旋转是指绕一点作为旋转中心，旋转θθ 角度的变换。 如上图所示，该正方形绕原点旋转了 θθ 角度。假设正方形的边长为 1，那么我们很容易可以得到如下的关系

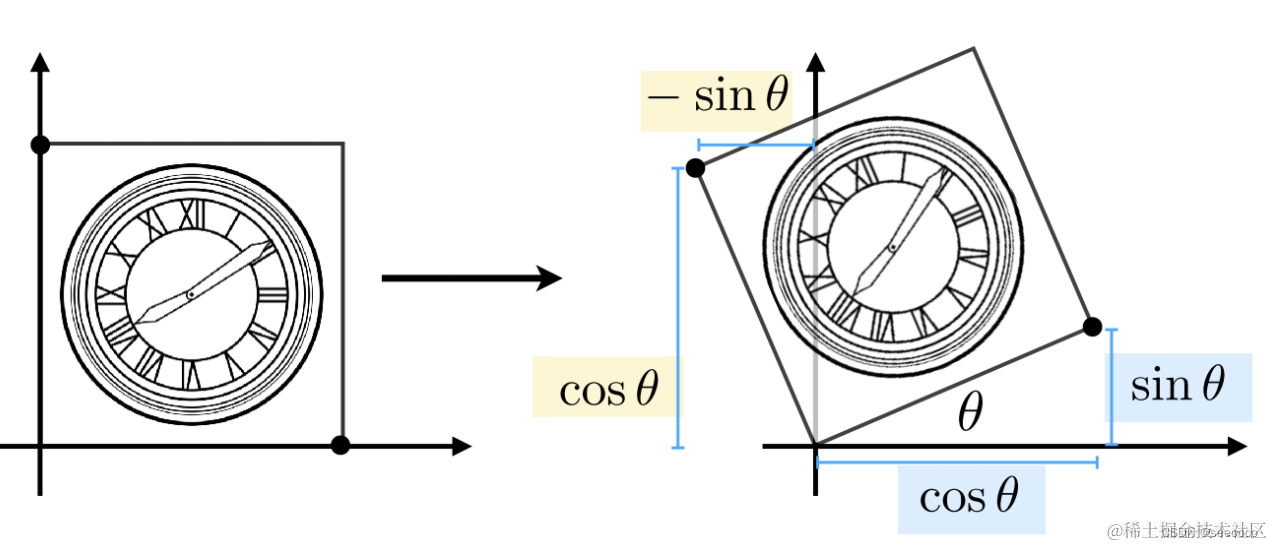
在这里插入图片描述

[x1y1]=[ABCD][x0y0]\begin{bmatrix} x_1 \\ y_1 \end{bmatrix} = \begin{bmatrix} A & B \\ C & D \end{bmatrix} \begin{bmatrix} x_0 \\ y_0 \end{bmatrix}

对于右下角的点，变换前的坐标是 (1,0)，变换后的坐标是 (cosθ,sinθ)， 我们可以得到如下的关系：

[cosθsinθ]=[ABCD][10]\begin{bmatrix} cos \theta \\ sin \theta \end{bmatrix} = \begin{bmatrix} A & B \\ C & D \end{bmatrix} \begin{bmatrix} 1 \\ 0 \end{bmatrix}

同理，对于左上角的点，变换前的坐标为 (0,1)，变换后的坐标为 (−sinθ,cosθ)，我们同样可以得到如下的关系

[−sinθcosθ]=[ABCD][01]\begin{bmatrix} -sin \theta \\ cos \theta \end{bmatrix} = \begin{bmatrix} A & B \\ C & D \end{bmatrix} \begin{bmatrix} 0 \\ 1 \end{bmatrix}

这样我们就得到了旋转矩阵

Rθ=[cosθ−sinθsinθcosθ]R_\theta = \begin{bmatrix} cos \theta & -sin \theta \\ sin \theta & cos \theta \end{bmatrix}

2.非线性变换

[1]平移变换

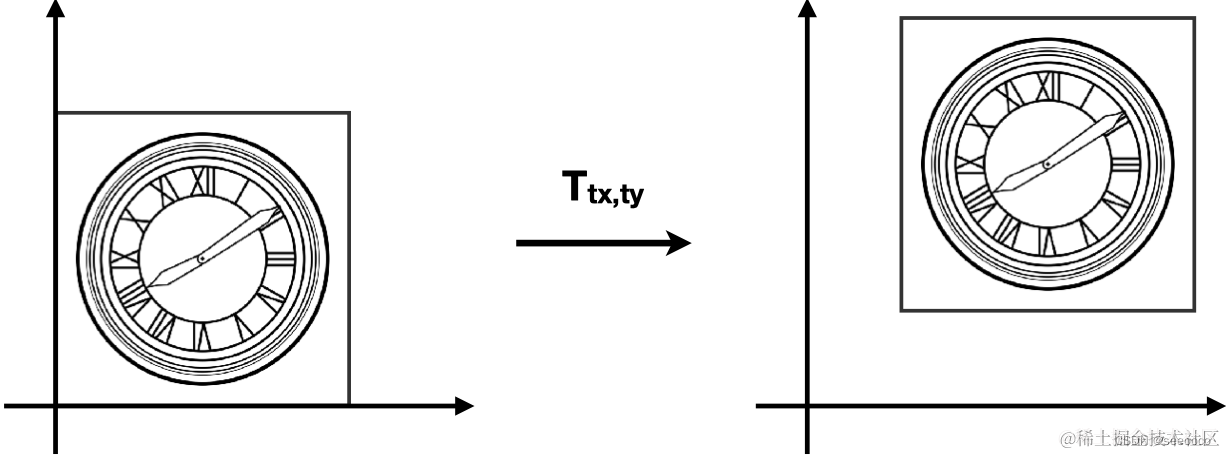
在这里插入图片描述

平移就是把 (x,y) 移动一段距离 (Tx,Ty) 然后得到一个新的坐标，即：

x1=x0+Txy1=y0+Tyx_1 = x_0 + T_x \\ y_1 = y_0 + T_y

因为他的变换不能使用矩阵来表示，所以它不是线性变换

[2]齐次坐标

一些非线性变换（例如下面的平移变换），并不能写成矩阵相乘的形式，只能写成下面的形式

[x1y1]=[ABCD][x0y0]+[TxTy]\begin{bmatrix} x_1 \\ y_1 \end{bmatrix} = \begin{bmatrix} A & B \\ C & D \end{bmatrix} \begin{bmatrix} x_0 \\ y_0 \end{bmatrix} + \begin{bmatrix} T_x \\ T_y \end{bmatrix}

我们希望有一个工具来统一所有变换为矩阵相乘的形式，这个工具就是 —— 齐次坐标。

通过添加多一个坐标来将非线性变换转化为线性变换

齐次坐标是再给点、向量增加一个 w 维度：

  • 2D 点： (x,y,1)(x,y,1)
  • 2D 向量： (x,y,0)(x,y,0)

当点、向量增加一个 w 维度之后，我们就可以把上述带有平移的变换写成如下的形式：

[x1y1w1]=[ABTxCDTy001][x0y0w0]\begin{bmatrix} x_1 \\ y_1 \\ w_1 \end{bmatrix} = \begin{bmatrix} A & B & T_x \\ C & D & T_y \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} x_0 \\ y_0 \\ w_0 \end{bmatrix}

因此，在齐次坐标下，我们就可以用一个矩阵来同时表示平移、旋转、缩放三种变换了。

并且，由于向量具有平移不变性，因此 w 为 0 的时候刚好能保证平移矩阵与向量相乘时，w 分量依然保持 0，如：

[x1y1w1]=[10Tx01Ty001][x0y00]=[x0+Txy0+Ty0]\begin{bmatrix} x_1 \\ y_1 \\ w_1 \end{bmatrix} = \begin{bmatrix} 1 & 0 & T_x \\ 0 & 1 & T_y \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} x_0 \\ y_0 \\ 0 \end{bmatrix} = \begin{bmatrix} x_0 + T_x \\ y_0 + T_y \\ 0 \end{bmatrix}

另外，对于 w 分量，还有些相关的结论：

  • 向量 + 向量 = 向量
    • 因为 w1+w2=0
  • 点 - 点 = 向量
    • 因为 w1−w2=0
  • 点 + 向量 = 点
    • 因为 w1+w2=1
  • 点 + 点 = 这两点的中点
    • 因为 w1+w2=2，在齐次坐标下，点的 w 分量为 1，所以结果要除以 2，得到的结果正是两点的中点位置

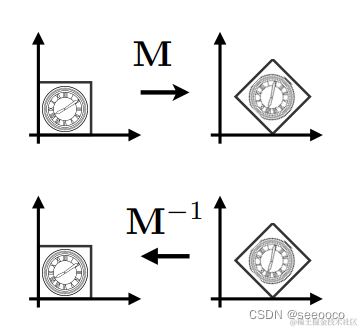
[3]逆变换

逆变换是指把已应用的变换还原的变换，在数学上是指变换矩阵的逆矩阵 M−1M^−1。

在这里插入图片描述

[4]仿射变换

仿射变换=线性变换+平移[x1y1]=[ABCD][x0y0]+[TxTy]仿射变换 = 线性变换 + 平移 \\ \begin{bmatrix} x_1 \\ y_1 \end{bmatrix} = \begin{bmatrix} A & B \\ C & D \end{bmatrix} \begin{bmatrix} x_0 \\ y_0 \end{bmatrix} + \begin{bmatrix} T_x \\ T_y \end{bmatrix}

其对应的齐次坐标的形式为：

[x1y11]=[ABTxCDTy001][x0y01]\begin{bmatrix} x_1 \\ y_1 \\ 1 \end{bmatrix} = \begin{bmatrix} A & B & T_x \\ C & D & T_y \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} x_0 \\ y_0 \\ 1 \end{bmatrix}

相对于仿射变换，齐次坐标有如下优点：

  • 可以用一个矩阵来表示平移、旋转、缩放三种变换。
  • 逆变换可以通过逆矩阵来表示。

我们可以把平移、旋转、缩放三种变换分别以齐次坐标的形式表示：

T(x,y)=[00Tx00Ty001]R(θ)=[cosθ−sinθ0sinθcosθ0001]S(x,y)=[Sx000Sy0001]T_{(x, y)} = \begin{bmatrix} 0 & 0 & T_x \\ 0 & 0 & T_y \\ 0 & 0 & 1 \end{bmatrix}\\ R_{(\theta)} = \begin{bmatrix} cos \theta & -sin \theta & 0 \\ sin \theta & cos \theta & 0 \\ 0 & 0 & 1 \end{bmatrix}\\ S_{(x, y)} = \begin{bmatrix} S_x & 0 & 0 \\ 0 & S_y & 0 \\ 0 & 0 & 1 \end{bmatrix}

在仿射变换下，变换的先后顺序是先进行线性变换，然后再进行平移变换。

3.三维变换

三维变换与二维变换类似，只是多了一个 z 维度。在齐次坐标下，

  • 3D 点表示为(x,y,z,1) (x,y,z,1)
  • 3D 向量表示为(x,y,z,0) (x,y,z,0)

通常，(x,y,z,w) 在 w≠0 时表示为一个 3D 的点，它的坐标为(x/w,y/w,z/w) (x/w,y/w,z/w)。

我们会用一个 4×4 的矩阵来表示三维变换

[x1y1z11]=[ABCTxDEFTyGHITz0001][x0y0z01]\begin{bmatrix} x_1 \\ y_1 \\ z_1 \\ 1 \end{bmatrix} = \begin{bmatrix} A & B & C & T_x \\ D & E & F & T_y \\ G & H & I & T_z \\ 0 & 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} x_0 \\ y_0 \\ z_0 \\ 1 \end{bmatrix}

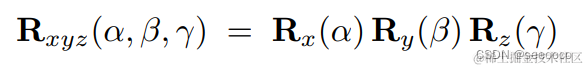
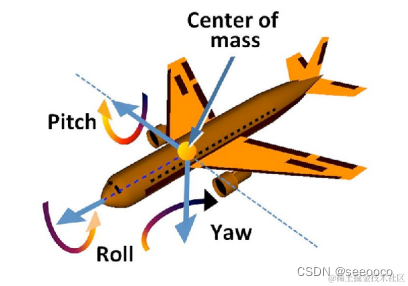
从 Rx、Ry、Rz 组成任何 3D 旋转？ 在这里插入图片描述

在这里插入图片描述

[1]正交矩阵

仔细观察一下旋转矩阵，和它的逆矩阵、转置矩阵，我们会发现一个有趣的现象：

Rθ=[cosθ−sinθsinθcosθ]R−θ=[cosθsinθ−sinθcosθ]RθT=[cosθsinθ−sinθcosθ]R_\theta = \begin{bmatrix} cos \theta & -sin \theta \\ sin \theta & cos \theta \end{bmatrix}\\ R_{-\theta} = \begin{bmatrix} cos \theta & sin \theta \\ -sin \theta & cos \theta \end{bmatrix}\\ {R_\theta}^T = \begin{bmatrix} cos \theta & sin \theta \\ -sin \theta & cos \theta \end{bmatrix}

旋转矩阵的逆矩阵与它的转置矩阵相同。我们可以利用旋转矩阵的这个性质来求它的逆矩阵。

另外，当一个矩阵的逆矩阵等于该矩阵的转置矩阵时，这个矩阵称为正交矩阵，因此旋转矩阵也是一个正交矩阵。

4.观测变换(Viewing transformation)

观测变换是为了把三维空间变换成二维空间（屏幕），它由两部分组成：

  • 视图变换 (View Transformation)
  • 投影变换 (Projection Transformation)
    • 正交投影
    • 透视投影

用一个例子来进入本节

想想如何拍照

  • 找个好地方安排人（模型变换model transformation）
  • 找到一个好的“角度”来放置相机（视图转换view transformation）
  • 茄子！ （投影变换projection transformation）

[1]View (视图) transformation

摄像机与物体的相对距离，会影响最终图像的效果。换句话说，无论是移动物体还是移动摄像机，只要保持两者的相对距离不变，那么我们就能得到相同的图像。

因此，我们可以把摄像机放到原点位置，朝向 -Z 方向，其他物体与摄像机保持相对位置不变，我们就能得到与世界空间下拍摄到的一样的图像了。

视图变换是用来把世界空间变换成摄像机空间。如下图所示：

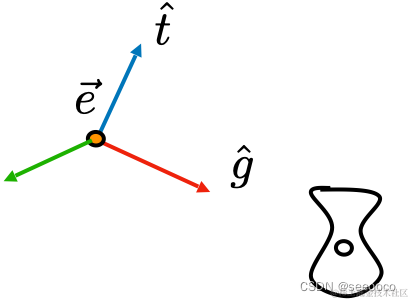
在这里插入图片描述

世界空间

  • e:观察者位置
  • t:视线
  • g:上方向

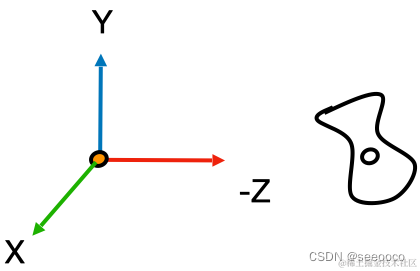
在这里插入图片描述

视觉空间

  • 观察者位置——>原点(0,0,0)(0,0,0)
  • 上方向——>Y
  • 视线——>-z

要确定视图变换，我们需要确定三个变量：

  1. 视线
  2. 视点
  3. 摄像机的上方向

如何将世界空间变换成视图空间呢？我们可以通过以下步骤：

  • Translates e to origin
  • Rotates g to -Z
  • Rotates t to Y
  • Rotates (g x t) To X

这些步骤就是视图变换（View Transformation）了，即：(RviewR_{view}为视点平移变换矩阵，)

Mview=Rview⋅TviewM_{view} = R_{view} \cdot T_{view}

世界空间——>视觉空间在数学上的实现

(1)Translate e to origin

Tview=[100−x 010−y 001−z 0001]T_{view} = \begin{bmatrix} 1 & 0 & 0 & -x \\\ 0 & 1 & 0 & -y \\\ 0 & 0 & 1 & -z \\\ 0 & 0 & 0 & 1 \end{bmatrix}

(2)Rotate g to -Z, t to Y, (g x t) To X

假设摄像机的的上方向为 t，同时往 g方向看，由于 e、t、g是摄像机的本地坐标系，因此三者相互垂直，所有有：

e^=g^×t^\hat e = \hat g \times \hat t

接下来需要求 RviewR_{view}，它是一个把摄像机的本地坐标系旋转成标准直角坐标系的变换，直接计算会比较复杂。

幸运的是，我们可以利用旋转矩阵是正交矩阵的特性，来求 RviewR_{view}

首先求它的逆矩阵：

Rview−1[xg^×t^xtx−g0 yg^×t^yty−g0 zg^×t^ztz−g0 0001]{R_{view}}^{-1} \begin{bmatrix} x_{\hat g \times \hat t} & x_t & x_{-g} & 0 \\\ y_{\hat g \times \hat t} & y_t & y_{-g} & 0 \\\ z_{\hat g \times \hat t} & z_t & z_{-g} & 0 \\\ 0 & 0 & 0 & 1 \end{bmatrix}

然后再进行一次转置操作即可：

Rview=Rview−1T=[xg^×t^yg^×t^zg^×t^0 xtytzt0 x−gy−gz−g0 0001]R_{view} = {{R_{view}}^{-1}}^T = \begin{bmatrix} x_{\hat g \times \hat t} & y_{\hat g \times \hat t} & z_{\hat g \times \hat t} & 0 \\\ x_t & y_t & z_t & 0 \\\ x_{-g} & y_{-g} & z_{-g} & 0 \\\ 0 & 0 & 0 & 1 \end{bmatrix}

最后，我们就可以得到视图矩阵：

Mview=Rview⋅Tview=[xg^×t^yg^×t^zg^×t^−x xtytzt−y x−gy−gz−g−z 0001]M_{view} = R_{view} \cdot T_{view} = \begin{bmatrix} x_{\hat g \times \hat t} & y_{\hat g \times \hat t} & z_{\hat g \times \hat t} & -x \\\ x_t & y_t & z_t & -y \\\ x_{-g} & y_{-g} & z_{-g} & -z \\\ 0 & 0 & 0 & 1 \end{bmatrix}

[2]Projection (投影) transformation

Projection in Computer Graphics

  • 3D to 2D
  • Orthographic projection
  • Perspective projection

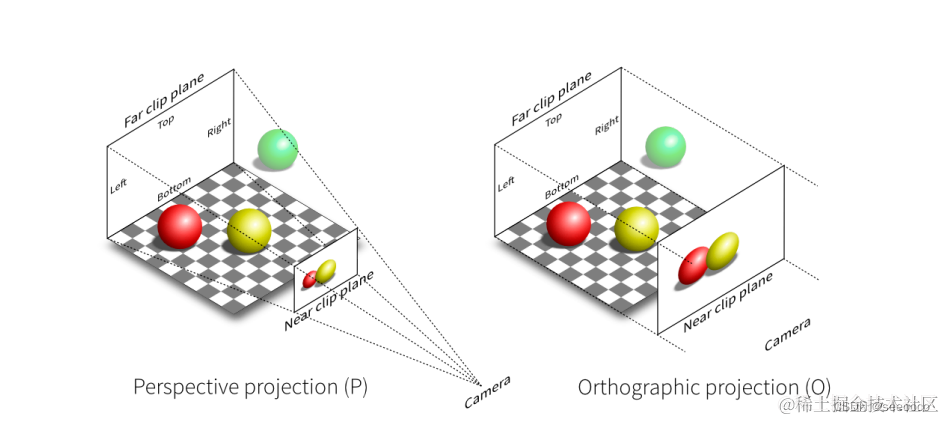
在这里插入图片描述

Orthographic (正交) projection

A simple way of understanding

  • Camera located at origin, looking at -Z, up at Y (looks familiar?)
  • Drop Z coordinate
  • Translate and scale the resulting rectangle to[−1,1]2 [-1, 1]^2(方便之后的计算)

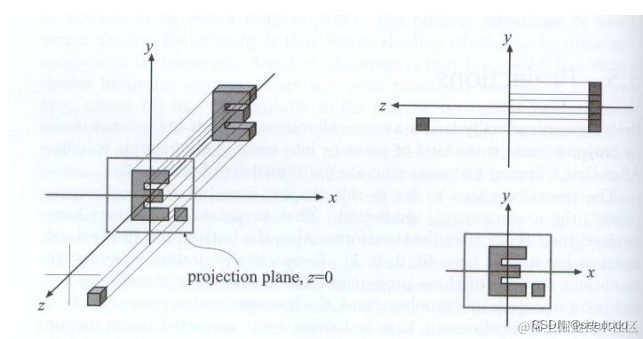
在这里插入图片描述

第二种理解正交投影的形式

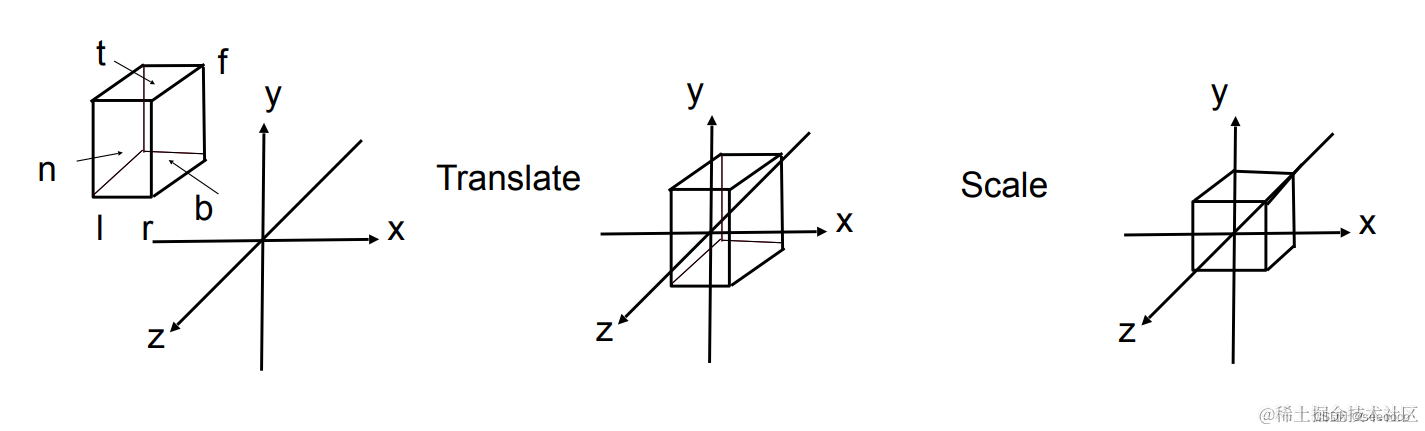
在这里插入图片描述

在图形学中，正交投影是把 [l,r]×[b,t]×[f,n][l,r]×[b,t]×[f,n] 构成的空间压缩成 [−1,1]3[−1,1]^3 的立方体中。

其中：

  • l = left
  • r = right
  • b = bottom
  • t = top
  • f = far
  • n = near

注意：因为摄像机是朝 -Z 方向的，所以 n > f

要确定正交投影矩阵，需要经过以下步骤：

  1. 把空间平移到原点（空间的中心与原点重合）
  2. 把空间压缩成 [−1,1]3[−1,1]^3

即：Mortho=Sortho⋅TorthoM_{ortho} = S_{ortho} \cdot T_{ortho}

由于我们知道空间的六个面，因此这个空间的中心就是：(l+r2,b+t2,f+n2)(\frac {l + r} 2, \frac {b + t} 2, \frac {f + n} 2)，那么就有

Tortho=[100−r+l2 010−t+b2 001−n+f2 0001]T_{ortho} = \begin{bmatrix} 1 & 0 & 0 & -{\frac {r + l} 2} \\\ 0 & 1 & 0 & -{\frac {t + b} 2} \\\ 0 & 0 & 1 & -{\frac {n + f} 2} \\\ 0 & 0 & 0 & 1 \end{bmatrix}

下一步就是压缩空间了，这一步骤相当于进行一次缩放，把当前空间缩放到大小为 2 的立方体。

以空间的 X 方向为例，其长度为 r−l，因此 X 方向的缩放因子就是:

(r−l)×Sx=2Sx=2r−l(r - l) \times S_x = 2 \\ S_x = \frac 2 {r - l}

同理可求出 SySy 和 SzSz，然后得到

Sortho=[2r−l000 02t−b00 002n−f0 0001]S_{ortho} = \begin{bmatrix} \frac 2 {r - l} & 0 & 0 & 0 \\\ 0 & \frac 2 {t - b} & 0 & 0 \\\ 0 & 0 & \frac 2 {n - f} & 0 \\\ 0 & 0 & 0 & 1 \end{bmatrix}

最后，正交投影矩阵为：

Mortho=Sortho⋅Tortho=[2r−l00−r+lr−l 02t−b0−t+bt−b 002n−f−n+fn−f 0001]M_{ortho} = S_{ortho} \cdot T_{ortho} = \begin{bmatrix} \frac 2 {r - l} & 0 & 0 & -{\frac {r + l} {r - l}} \\\ 0 & \frac 2 {t - b} & 0 & -{\frac {t + b} {t - b}} \\\ 0 & 0 & \frac 2 {n - f} & -{\frac {n + f} {n - f}} \\\ 0 & 0 & 0 & 1 \end{bmatrix}

因为正射投影产生的可视空间是个规则的立方体，所以我们只需要知道两个边界的点就可以确定整个可视空间的范围了

Perspective (透视) projection

  • Most common in Computer Graphics, art, visual system
  • Further objects are smaller（近大远小）
  • Parallel lines not parallel; converge to single point

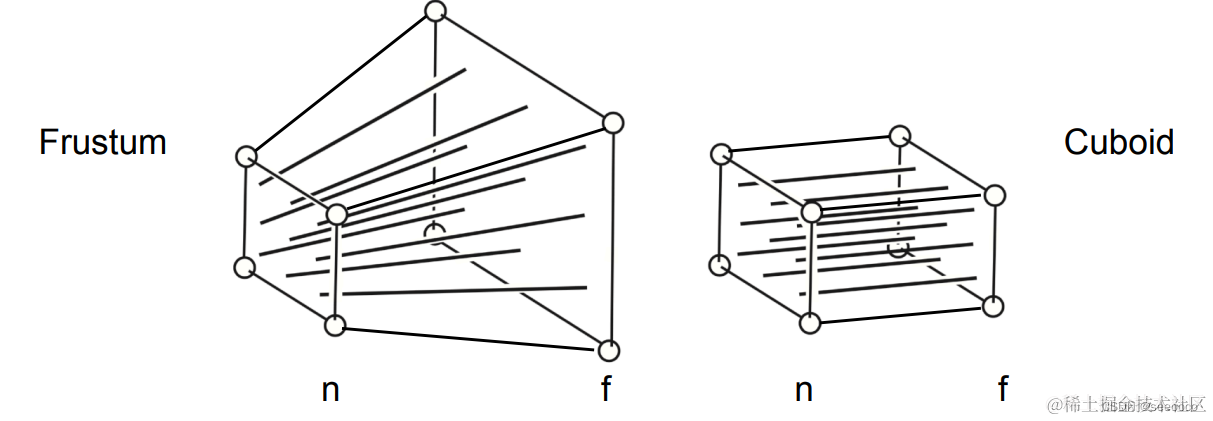
在这里插入图片描述

透视投影与正交投影类似，也是经过类似的步骤：

  1. 把空间平移到原点
  2. 把空间压缩成长方体（近平面不变，压缩远平面）
  3. 把空间压缩成[−1,1]3 [−1,1]^3 的立方体（进行一次正交投影）

相比正交投影，透视投影多了一个步骤，就是把视锥体变换成长方体，这个变换暂且叫做Mp−>oMp−>o。 要计算这个变换，我们需要先知道这个变换过程发生了什么。

下图是 YZ 平面的截面：

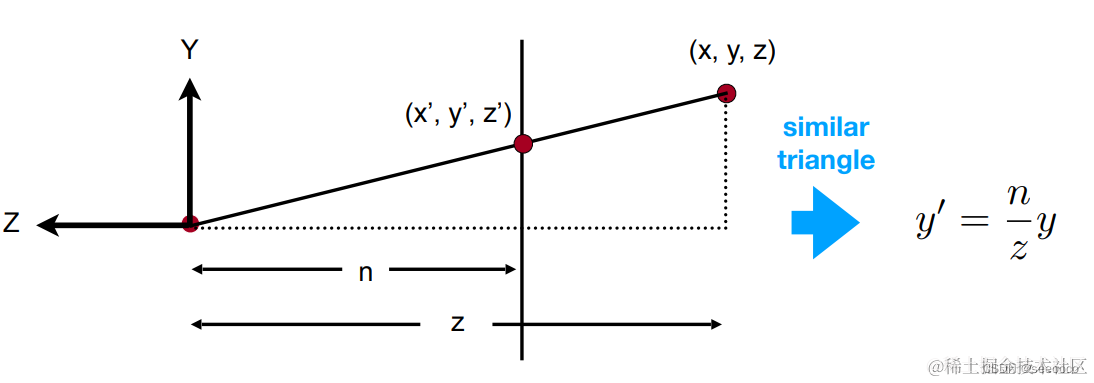
在这里插入图片描述

经过压缩后，对于 y 坐标，空间中的一点(x,y,z)(x,y,z)会变成(x,y′,z) (x,y′,z)，根据相似三角形的性质，我们会得到如下的等式：

nz=y′yy′=nzy\frac n z = \frac {y^{\prime}} y \\ y^{\prime} = \frac n z y

同理，对于 x 坐标，我们也能得到类似的等式：

x′=nzxx^{\prime} = \frac n z x

然后，我们就能得到如下的结果：

Mpersp−>ortho[xyz1]=[nxznyzunknow1]M_{persp -> ortho}\begin{bmatrix} x \\ y \\ z \\ 1\end{bmatrix}=\begin{bmatrix} \frac {nx} z \\ \frac {ny} z \\ unknow \\ 1\end{bmatrix}

再稍微变换一下写法（乘以z），我们能得到：

Mpersp−>ortho[xyz1]=[nxnyunknowz]M_{persp -> ortho}\begin{bmatrix} x \\ y \\ z \\ 1\end{bmatrix}=\begin{bmatrix} nx \\ ny \\ unknow \\ z\end{bmatrix}

计算一下 Mpersp−>orthoMpersp−>ortho，矩阵的第一行，可以得到：

ax+by+cz+d=nxax + by + cz + d = nx

于是有

a=nb=0c=0d=0a = n \\ b = 0 \\ c = 0 \\ d = 0

我们可以用同样的方法去计算矩阵的其它行，于是就能得到矩阵的雏形：

Mpersp−>ortho=[n000 0n00 ???? 0010]M_{persp -> ortho} = \begin{bmatrix} n & 0 & 0 & 0 \\\ 0 & n & 0 & 0 \\\ ? & ? & ? & ? \\\ 0 & 0 & 1 & 0 \end{bmatrix}

矩阵的第三行是表示 z 方向的变换的，而我们知道有两个事实：

  • 任何在近平面的点，都不会发生变化，即：
    [????][xyn1]=[xyn1]=[nxnyn2n] \begin{bmatrix}? & ? & ? & ? \end{bmatrix} \begin{bmatrix} x \\ y \\ n \\ 1\end{bmatrix}= \begin{bmatrix} x \\ y \\ n \\ 1\end{bmatrix}= \begin{bmatrix} nx \\ ny \\ n^2 \\ n\end{bmatrix}

和刚才一样代入计算（因为刚才乘以过 zz，所以右边要用 n2n^2，下面的 f2f^2 同理）：

ax+by+cn+d=n2ax+by+cn+d=n^2

于是得到矩阵第三行的四个元素分别是：

[00AB]\begin{bmatrix} 0 & 0 & A & B \end{bmatrix}
  • 任何在远平面上的店，z 都不会发生变化。我们取远平片中的一个中心点 (0,0,f,1) ，它在空间压缩前后都不会发生变化，那么：
[00AB][00f1]=[00f1]==[00f2f]\begin{bmatrix} 0 & 0 & A & B \end{bmatrix} \begin{bmatrix} 0 \\ 0 \\ f \\ 1 \end{bmatrix}= \begin{bmatrix} 0 \\ 0 \\ f \\ 1\end{bmatrix} == \begin{bmatrix} 0 \\ 0 \\ f^2 \\ f\end{bmatrix}

联立方程组：

An+B=n2Af+B=f2An+B=n^2 \\ Af+B=f^2

解得：

A=n+fB=−nfA=n+f \\ B=−nf

因此，我们要求的矩阵为：

Mpersp−>ortho=[n000 0n00 00n+f−nf 0010]M_{persp -> ortho}= \begin{bmatrix} n & 0 & 0 & 0 \\\ 0 & n & 0 & 0 \\\ 0 & 0 & n + f & -nf \\\ 0 & 0 & 1 & 0 \end{bmatrix}

所以，投影矩阵为：

Mpersp=MorthoMpersp−>orthoMpersp=MorthoMpersp−>ortho

最后的问题就是 MorthoMortho（正交投影） 了。对于这个正交投影，我们只知道 [f,n]，还缺少 [l,r] 和 [b,t]，但我们可以通过其他途径来计算出这些需要的值。

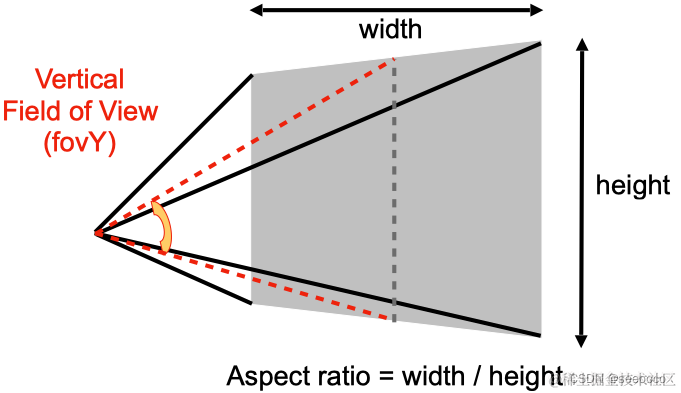
对于透视投影，还有两个重要的概念，那就是 field of view(fov) 和 aspect ratio。 在这里插入图片描述

fov 是指视野范围，分为 fovY 和 fovX，两者可以相互推导。

aspect ratio 是指近平面的宽高比。

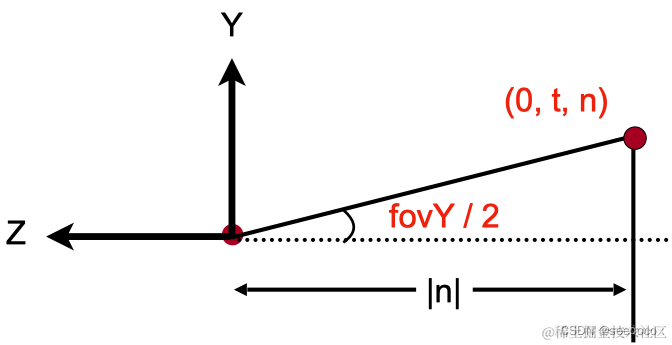
在这里插入图片描述

根据三角函数，我们可以知道：

tanfovY2=t∣n∣tan {\frac {fovY} 2} = \frac t {|n|}

另外，根据宽高比的定义，我们可以得出：

aspect=widthheight=2r2t=rtaspect = \frac {width} {height} = \frac {2r} {2t} = \frac r t

联立方程可得：

t=∣n∣⋅tanfovY2r=aspect⋅tb=−tl=−rt = |n| \cdot tan {\frac {fovY} 2} \\ r = aspect \cdot t\\ b = -t\\ l = -r

这样，我们就把所需要的值都计算出来了，直接带入上面的正交矩阵公式即可

avatar
文章
阅读
粉丝