开启掘金成长之旅!这是我参与「掘金日新计划 · 2 月更文挑战」的第 32 天,点击查看活动详情
(本文是第32篇活动文章)
2. 香农信息量/自信息I
连续型随机变量:
I(x)=−log2p(x)=log2p(x)1
这时香农信息量的单位为比特。(如果非连续型随机变量,则为某一具体随机事件的概率,其他的同上)
香农信息量用于刻画消除随机变量在处的不确定性所需的信息量的大小。
(本节参考香农信息量__寒潭雁影的博客-CSDN博客一文,该文中还有用数据压缩来介绍为何要这么定义,我没咋看懂,但是觉得很有意思,可供参考)
对数以e为底,单位是纳特(nat)
3. 信息熵
用期望评估整体系统的信息量:“事件香农信息量×事件概率”的累加
H(p)=E[I(x)]=E[−log(p(x))]
信息熵公式
(对于连续型随机变量):
H(p)=H(X)=Ex∼p(x)[−logp(x)]=−∫p(x)logp(x)dx
(对于离散型随机变量):
H(p)=H(X)=Ex∼p(x)[−logp(x)]=−i=1∑np(xi)logp(xi)
注意,我们前面在说明的时候log是以2为底的,但是一般情况下在神经网络中,默认以e为底,这样算出来的香农信息量虽然不是最小的可用于完整表示事件的比特数,但对于信息熵的含义来说是区别不大的。其实只要这个底数是大于1的,都能用来表达信息熵的大小。
4. 相对熵/KL散度/信息散度
两个概率分布间差异的非对称性度量。
在信息论中,相对熵等价于两个概率分布的信息熵的差值,若其中一个概率分布为真实分布( p(xi) ),另一个为理论(拟合)分布( q(xi) ),则此时相对熵等于交叉熵与真实分布的信息熵之差,表示使用理论分布拟合真实分布时产生的信息损耗 。
DKL(p∥q)=i=1∑N[p(xi)logp(xi)−p(xi)logq(xi)]
有一种理解是:信息量变成了−log(q),但事件概率还是原先的 p,所以会变成那个公式
假设理论拟合出来的事件概率分布跟真实的一模一样,那么这玩意就等于真实事件的信息熵,这一点显而易见。
假设拟合的不是特别好,那么这个玩意会比真实事件的信息熵大(这个在相对熵(KL散度)__寒潭雁影的博客-CSDN博客_kl三都一文中有证明,感觉还是比较好证的)。
也就是在理论拟合出来的事件概率分布跟真实的一模一样的时候,相对熵等于0。而拟合出来不太一样的时候,相对熵大于0。这个性质很关键,因为它正是深度学习梯度下降法需要的特性。假设神经网络拟合完美了,那么它就不再梯度下降,而不完美则因为它大于0而继续下降。

(相对熵(KL散度)__寒潭雁影的博客-CSDN博客_kl三都一文中还介绍了为什么用相对熵衍生出的交叉熵而不是均方差作为损失函数来训练神经网络,主要是关心梯度消失问题。相关的分析博文还可以参考,我只浏览过一遍还没有细看:1. 深度学习1---最简单的全连接神经网络__寒潭雁影的博客-CSDN博客_全连接神经网络实例 2. 一文弄懂神经网络中的反向传播法——BackPropagation - Charlotte77 - 博客园 3. 神经网络中w,b参数的作用(为何需要偏置b的解释)_AI_盲的博客-CSDN博客_神经元 为什么要有偏置)
交叉熵:
Hq(p)=∑xp(x)logq(x)1
KL散度=交叉熵-信息熵
D_{KL}(p∥q)&=H_q(p)-H(p)\\
&=\sum_xp(x)\log\frac{1}{q(x)}-\bigg(-\sum_xp(x)\log p(x)\bigg)\\
&=\displaystyle\sum\limits_{i=1}^N\Big[p(x_i)\log p(x_i)−p(x_i)\log q(x_i)\Big]
\end{aligned}$$
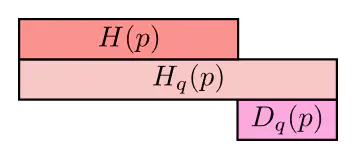
第一行表示p所含的信息量/平均编码长度$H(p)$;
第二行是cross-entropy,即用q来编码p所含的信息量/平均编码长度|或者称之为q对p的cross-entropy;
第三行是上面两者之间的差值,即q对p的KL距离,KL距离越大说明差值越大,说明两个分布的差异越大。
(注意这三者都是非负的。上面说的KL和cross-entropy是两个不同分布之间的距离度量,因此用$H(p)$来表示熵。如果是测量同一分布中两个变量相互影响的关系,则一般用$H(X)$来表示熵,如[联合信息熵和条件信息熵 - 简书](https://www.jianshu.com/p/f853fa7344b5)(我还没看))
这一部分我还没看的参考资料:1. [【机器学习】信息量,信息熵,交叉熵,KL散度和互信息(信息增益)_哈乐笑的博客-CSDN博客](https://blog.csdn.net/haolexiao/article/details/70142571)(这一篇公式符号似乎有问题) 2. [熵 (信息论) - 维基百科,自由的百科全书](https://zh.wikipedia.org/wiki/%E7%86%B5_(%E4%BF%A1%E6%81%AF%E8%AE%BA))