一、概述

粒子滤波（Particle Filter）是动态模型的非线性，非高斯的版本，也就是说$z_t$和$z_{t-1}$、$x_t$和$z_t$的关系是非线性的，其噪声也是非高斯的：

$$z_{t}=g(z_{t-1},\mu ,\varepsilon )\\ x_{t}=h(z_{t},\mu ,\delta )$$

卡尔曼滤波的概率分布可以直接通过高斯分布的性质解得，然而，对于粒子滤波，由于其状态转移概率和发射概率是任意的，我们无法直接得到其概率分布。因此，我们需要采用采样的方法进行估计。在实际应用中，我们通常更关注的是概率分布关于某函数的期望，而非概率分布本身。因此，本文将主要介绍如何通过采样的方法来求某个函数依概率分布的期望。

二、序列重要性采样

对于分布$p(z)$，要求期望$E_{p(z)}[f(z)]$，重要性采样（Importance Sampling）的方法是引入一个新的分布$q(z)$，然后对$q(z)$进行采样，其做法如下：

$$E_{p(z)}[f(z)]=\int f(z)\cdot p(z)\mathrm{d}z\\ =\int f(z)\cdot \frac{p(z)}{q(z)}\cdot q(z)\mathrm{d}z\\ \approx \frac{1}{N}\sum_{i=1}^{N}f(z_{i})\cdot \underset{权重}{\underbrace{\frac{p(z_{i})}{q(z_{i})}}}\\ z_{i}\sim q(z),i=1,2,\cdots ,N$$

在滤波问题中，关心的概率分布是$p(z_{t}|x_{1:t})$，权重就是：

$$w_{t}^{(i)}=\frac{p(z_{t}^{(i)}|x_{1:t})}{q(z_{t}^{(i)}|x_{1:t})},i=1,2,\cdots ,N$$

使用重要性采样的一个挑战是计算量过大。在每个时刻，我们都需要进行$N$次采样，而权重的分子这一项的计算是非常复杂的。因此，我们希望找到一个$w_{t}^{(i)}$与$w_{t-1}^{(i)}$之间的递推关系来简化这个过程。这就引出了序列重要性采样（Sequential Importance Sampling，SIS) 的概念。

在SIS中，我们并不直接使用$p(z_{t}^{(i)}|x_{1:t})$进行采样，而是使用$p(z_{1:t}^{(i)}|x_{1:t})$。这样做的目的是为了简化计算。我们可以使用$p(z_{1:t}^{(i)}|x_{1:t})$进行采样，是因为它满足一定的条件：

$$w_{t}^{(i)}\propto \frac{p(z_{1:t}^{(i)}|x_{1:t})}{q(z_{1:t}^{(i)}|x_{1:t})}$$

现在我们首先要找到$p(z_{1:t}|x_{1:t})$与$p(z_{1:t-1}|x_{1:t-1})$之间的递推关系：

$${\color{Red}{p(z_{1:t}|x_{1:t})}}=\frac{p(z_{1:t},x_{1:t})}{p(x_{1:t})}\\ =\frac{1}{C}p(z_{1:t},x_{1:t})\\ =\frac{1}{C}p(x_{t}|z_{1:t},x_{1:t-1})\cdot p(z_{1:t},x_{1:t-1})\\ =\frac{1}{C}p(x_{t}|z_{t})\cdot p(z_{t}|z_{1:t-1},x_{1:t-1})\cdot p(z_{1:t-1},x_{1:t-1})\\ =\frac{1}{C}p(x_{t}|z_{t})\cdot p(z_{t}|z_{t-1})\cdot p(z_{1:t-1}|x_{1:t-1})\cdot \underset{D}{\underbrace{p(x_{1:t-1})}}\\ =\frac{D}{C}p(x_{t}|z_{t})\cdot p(z_{t}|z_{t-1})\cdot {\color{Red}{p(z_{1:t-1}|x_{1:t-1})}}$$

由于$q(z_{1:t}|x_{1:t})$是我们指定的，因此可以指定：

$${\color{Red}{q(z_{1:t}|x_{1:t})}}=q(z_{t}|z_{1:t-1},x_{1:t})\cdot {\color{Red}{q(z_{1:t-1}|x_{1:t-1})}}$$

所以有：

$$w_{t}^{(i)}\propto \frac{p(z_{1:t}^{(i)}|x_{1:t})}{q(z_{1:t}^{(i)}|x_{1:t})}\propto \frac{p(x_{t}|z_{t}^{(i)})\cdot p(z_{t}^{(i)}|z_{t-1}^{(i)})\cdot {\color{Red}{p(z_{1:t-1}^{(i)}|x_{1:t-1})}}}{q(z_{t}^{(i)}|z_{1:t-1}^{(i)},x_{1:t})\cdot {\color{Red}{q(z_{1:t-1}^{(i)}|x_{1:t-1})}}}=\frac{p(x_{t}|z_{t}^{(i)})\cdot p(z_{t}^{(i)}|z_{t-1}^{(i)})}{q(z_{t}^{(i)}|z_{1:t-1}^{(i)},x_{1:t})}\cdot w_{t-1}^{(i)}$$

总结一下，SIS的迭代过程如下：

前提：

$t-1$时刻完成采样并计算得到权重

$t$时刻：$for\;\; i = 1, ... , N$

①根据$q(z_{t}|z_{1:t-1}^{(i)},x_{1:t})$完成采样得到$z_{t}^{(i)}$，并且计算权重$w_{t}^{(i)}$；

②对权重进行归一化，$w_{t}^{(i)}\rightarrow \hat{w}_{t}^{(i)},\sum_{i=1}^{N}\hat{w}_{t}^{(i)}=1$。

三、重要性重采样

为了解决权值退化的问题，我们引入了重要性重采样(Sampling Importance Resampling,SIR)算法。这是在SIS的基础上进行改进的算法，它增加了两个部分：一个是重采样，另一个是特定的$q(z_{t}|z_{1:t-1},x_{1:t})$概率分布。

1. 重采样

SIS算法可能会出现权值退化的现象，即在一段时间后，大部分权重都接近于$0$。这主要是由于维度灾难的问题，在高维空间中需要大量的样本。通过使用重采样，我们可以缓解这一现象。

下面我们以$N=3$为例来解释重采样的过程。在下表中，我们展示了3个采样粒子的权重（归一化后的权重可以理解为pdf)，并且计算了pdf的cdf：

	$z^{(1)}$	$z^{(2)}$	$z^{(3)}$
pdf	0.1	0.1	0.8
cdf	0.1	0.2	1

画出例子的cdf图像如下：

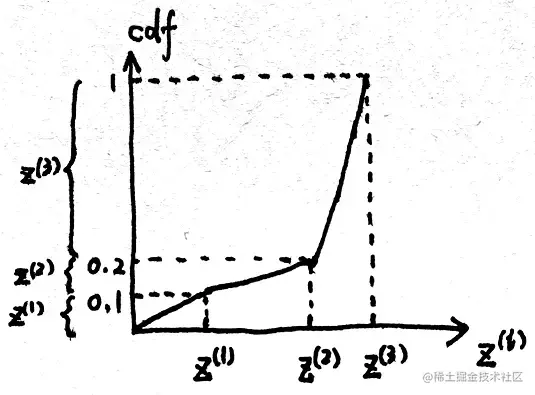
重采样是指在均匀分布$u\sim U(0,1)$上进行采样，然后依照cdf找到对应的新的粒子$z^{(i)}$，意味着将原有的概率值重新变为等面积的样本点，另外，重采样以后的新的权重$\hat{\hat{w}}=\frac{1}{N}$。

在SIS的基础上加上重采样，就是基本的粒子滤波算法（Basic Particle Filter）。

2. 选择合适的提议分布

选择恰当的提议分布也是一种解决权重衰减的方法。这里一个常用的选择就是：

$$q(z_{t}|z_{1:t-1},x_{1:t})=p(z_{t}|z_{t-1})$$

则此时的权重$w_{t}^{(i)}$的计算公式就变为了：

$$w_{t}^{(i)}=\frac{p(x_{t}|z_{t}^{(i)})\cdot p(z_{t}^{(i)}|z_{t-1}^{(i)})}{q(z_{t}^{(i)}|z_{1:t-1}^{(i)},x_{1:t})}\cdot w_{t-1}^{(i)}=\frac{p(x_{t}|z_{t}^{(i)})\cdot {\color{Red}{p(z_{t}^{(i)}|z_{t-1}^{(i)})}}}{{\color{Red}{p(z_{t}^{(i)}|z_{t-1}^{(i)})}}}\cdot w_{t-1}^{(i)}=p(x_{t}|z_{t}^{(i)})\cdot w_{t-1}^{(i)}$$

这个策略被称为生成与测试策略。在生成阶段，我们通过 $p\left(z_t \mid z_{t-1}^{(i)}\right)$ 产生一个 $p\left(x_t \mid z_t^{(i)}\right)$，然后将它们相乘以计算新的权重 $w_t^{(i)}$。随后，在测试阶段，如果生成的样本 $z^{(i)}$ 对应的 $p\left(x_t \mid z_t^{(i)}\right)$ 较大，那么新的权重 $w_t^{(i)}$ 也会相应增大，这表明样本 $z^{(i)}$ 是一个较好的选择。

3. 算法

在SIS的基础上加上重采样和上述特定的提议分布就得到了SIR算法，其迭代的流程是这样的：

前提：$t-1$时刻完成采样并计算得到权重 $t$时刻：

①根据$q(z_{t}|z_{1:t-1}^{(i)},x_{1:t})=p(z_{t}|z_{t-1}^{(i)})$完成采样得到$z_{t}^{(i)}$，并且计算权重$w_{t}^{(i)}=p(x_{t}|z_{t}^{(i)})\cdot w_{t-1}^{(i)}$；

②对权重进行归一化，$w_{t}^{(i)}\rightarrow \hat{w}_{t}^{(i)},\sum_{i=1}^{N}\hat{w}_{t}^{(i)}=1$。

③重采样

“开启掘金成长之旅！这是我参与「掘金日新计划 · 2 月更文挑战」的第 15 天，点击查看活动详情”