1. 琴生不等式

在这里插入图片描述

证明加权形式（令 $a_{1}=a_{2}=\cdots=a_{n}=\dfrac{1}{n}$ 即为一般形式）：

首先证明 $a_1x_1+a_2x_2+\dots+a_nx_n$ 仍然在 $[a,b]$ 内（另一种证明思路见百度百科，即参考资料链接1）：不妨设 $x_1\geq x_2\geq\dots\geq x_n$ $a_1x_1+a_2x_2+\dots+a_nx_n=a_1(x_1-x_2)+(a_1+a_2)(x_2-x_3)+\dots+(a_1+a_2+\dots+a_{n-1})(x_{n-1}-x_n)+(a_1+a_2+\dots+a_n)x_n$ （这个我自己想是想不出来的，但是我可以理解。大概展开是这样的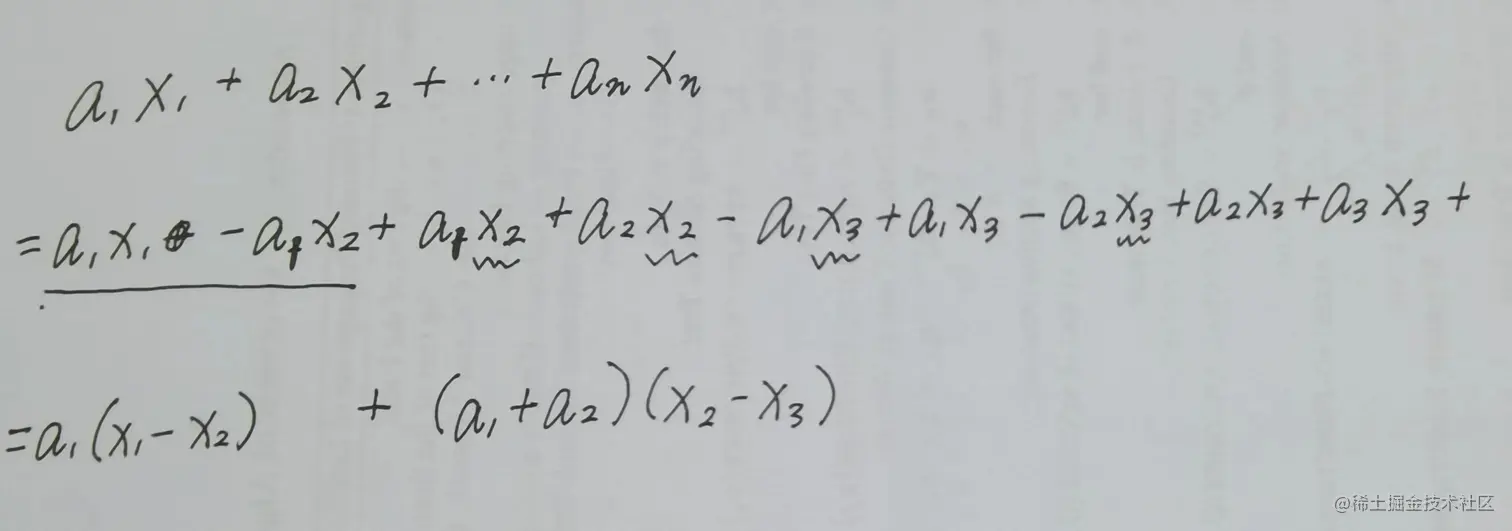：）在这里插入图片描述每一项的值都是 $[0,x_i-x_{i+1}]$ ，最后一项是 $x_n$ ，所以整个多项式的取值范围是 $[x_n,x_1]$ （右界一般情况下能不能取到我还没琢磨明白，反正 $a_1=1$ 时肯定可以，别的情况我还没想到），显然是在 $[a,b]$ 范围内的

用数学归纳法证明不等式： ①当 $n=1$ 时 $f(x)\leq f(x)$ 显然成立 ②当 $n=2$ 时：设 $x_1\leq x_2$ 函数曲线在 $(x_1,f(x_1)),(x_2,f(x_2))$ 所构成的直线之下，设这条直线为 $g(x)=mx+n$ 则 $a_1f(x_1)+a_2f(x_2)=a_1(mx_1+n)+a_2(mx_2+n)=m(a_1x_1+a_2x_2)+n=g(a_1x_1+a_2x_2)$ 所以 $a_1f(x_1)+a_2f(x_2)=g(a_1x_1+a_2x_2)\geq f(a_1x_1+a_2x_2)$ 得证 ③假设对任意 $n\geq2$ 不等式都成立，即 $f(a_1x_1+a_2x_2+a_3x_3+\dots+a_nx_n)\leq a_1f(x_1)+a_2f(x_2)+\dots+a_nf(x_n)$ 则当 $n=n+1$ 时：

\begin{aligned} f(a_1x_1+a_2x_2+a_3x_1+\dots+a_nx_n+a_{n+1}x_{n+1})&=f\Big((a_1+a_2+\cdots+a_n)\frac{a_1x_1+a_2x_2+a_3x_1+\dots+a_nx_n}{a_1+a_2+\cdots+a_n}+a_{n+1}x_{n+1}\Big)\\ &\leq(a_1+a_2+\cdots+a_n)f\big(\frac{a_1x_1+a_2x_2+a_3x_1+\dots+a_nx_n}{a_1+a_2+\cdots+a_n}\big)+a_{n+1}f(x_{n+1})\\ &=(a_1+a_2+\cdots+a_n)f\big(\frac{a_1x_1}{a_1+a_2+\cdots+a_n}+\frac{a_2x_2}{a_1+a_2+\cdots+a_n}+\dots+\frac{a_nx_n}{a_1+a_2+\cdots+a_n}\big)+a_{n+1}f(x_{n+1})\\ &\leq(a_1+a_2+\cdots+a_n)\Big[\frac{a_1f(x_1)}{a_1+a_2+\cdots+a_n}+\frac{a_2f(x_2)}{a_1+a_2+\cdots+a_n}+\dots+\frac{a_nf(x_n)}{a_1+a_2+\cdots+a_n}\Big]+a_{n+1}f(x_{n+1})\\ &=a_1f(x_1)+a_2f(x_2)+\dots+a_nf(x_n)+a_{n+1}f(x_{n+1}) \end{aligned}

不等式得证

变分推断（variational inference）/variational EM (1)

1. 琴生不等式