开启掘金成长之旅！这是我参与「掘金日新计划 · 2 月更文挑战」的第 30 天，点击查看活动详情

3. HMM参数介绍和求解方法

观测序列：观测概率矩阵B（状态生成观测的概率） 未观测的状态序列：初始状态概率向量$\pi$（处于状态的概率） + 状态转移概率矩阵A

$\lambda=(A,B,\pi)$

HMM：$P(O|\lambda)=\sum\limits_IP(O,I|\lambda)=\sum\limits_IP(O|I,\lambda)P(I|\lambda)$（其中I为标注序列）

1. 训练，已知$O$求$\lambda$：其中I为标注序列，在公式中是隐变量，因此可用EM算法¹求解上式的模型参数$\lambda$。具体步骤：
   1. 初始化$\overline\lambda$
   2. 观测变量和隐变量的对数似然函数：$\log P(O,I|\lambda)=\pi_{i_1}b_{i_1}(o_1)a_{i_1i_2}b_{i_2}(o_2)\cdots a_{i_{T-1}i_T}b_{i_T}(o_T)$（初始状态×生成观测的概率×状态转移概率×生成观测的概率…）
   3. E：对隐变量求期望 $Q(\lambda,\overline\lambda)=\sum\limits_I\log P(O,I|\lambda)P(O,I|\overline\lambda)=\sum\limits_I\log\pi_{i_1}P(O,I|\overline\lambda)+\sum\limits_I(\sum\limits_{t=1}^{T-1}\log a_{i_ti_{t+1}})P(O,I|\overline\lambda)+\sum\limits_I(\sum\limits_{t=1}^T\log b_{i_t}(o_t))P(O,I|\overline\lambda)$
   4. M：求使$Q$取极大值的$\lambda=(A,B,\pi)$ 求偏导数并使其等于0，有：$\dfrac{\partial Q(\lambda,\overline\lambda)}{\partial\pi_i}=\dfrac{\partial Q(\lambda,\overline\lambda)}{\partial a_{ij}}=\dfrac{\partial Q(\lambda,\overline\lambda)}{\partial b_j(k)}0$ 约束条件为初始状态概率分布的和等于1，即：$\sum\limits_{i=1}^N\pi_i=1$ 状态已知的情况下，观测概率分布的和等于1，即：$\sum\limits_{k=1}^Mb_j(k)=1$ 得到$\pi_i,a_{ij},b_j(k)$的值，即更新$\lambda$
   5. 重复步骤3、4
2. 计算观测序列出现的概率（N是总的状态数）
   1. 枚举法：$O(TN^T)$
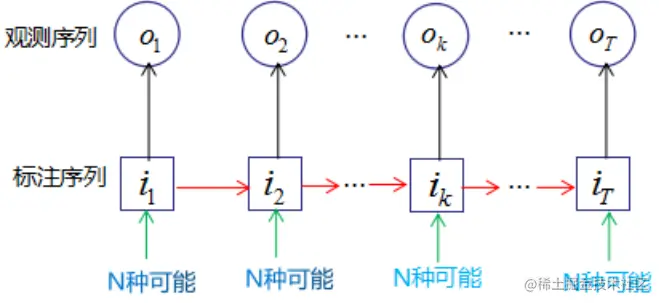
   2. 递推法：$O(TN^2)$ 状态为$q_i$的前向概率$\alpha_t(i)$（生成给定长度为t的观测序列，且t状态是$q_i$的概率）：$\alpha_t(i)=P(o_1,o_2,\dots,o_t,i_t=q_i|\lambda)$
      t=1时：$\alpha_1(i)=\pi_ib_i(o_1),i=1,2,\dots,N$（初始得到该状态×该状态生出该观测） $P(o_1|\lambda)=\sum\limits^N_{i=1}\alpha_{1}(i)$（在所有状态下生成该观测的概率加总）
      递推，对于$t=1,2,\dots,T-1$ $\alpha_{t+1}(i)=\Bigg[\sum\limits_{j=1}^N\alpha_t(j)a_{ji}\Bigg]b_i(o_{t+1}),i=1,2,\dots,N$（上一次生成状态j，状态j转移为状态i，状态i生成观测的概率） $P(o_1,o_2,\dots,o_{t+1}|\lambda)=\sum\limits_{i=1}^N\alpha_{t+1}(i)$
      当t=T时： $P(O|\lambda)=\sum\limits_{i=1}^N\alpha_T(i)$
      算法复杂度（感觉图把i写成j了）：
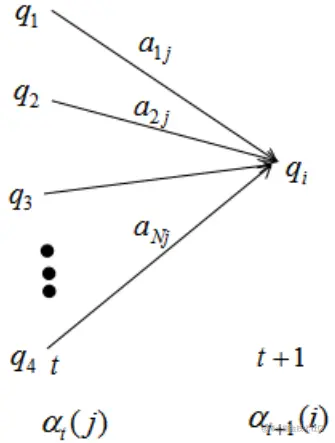
      $\alpha_{t+1}(i)=\sum\limits_{j=1}^N\alpha_t(j)a_{ji}$（a是状态转移概率） 因此从t到t+1时刻的计算量为$O(N^2)$ 对于观测序列长度为T：$O(TN^2)$
3. 模式匹配中的维特比算法（动态规划） 给定$\lambda$（模型参数）和$O$（观测序列），预测最有可能的状态序列 算法思想：若 t 时刻最有可能的状态序列$I=(i_1,i_2,\dots,i_t^*)$通过$i_t^*$，则从t时刻到T时刻的最优路径一定包括$i_t^*$。我们利用这一思想确定了最优状态序列的最后一个时刻的状态$i_T$，然后利用该状态回溯时刻$t=1,2,\dots,T-1$的最优状态
   示例： 已知模型$\lambda=(A,B,\pi)$，观测集合$V=\{O_1,O_2\}$，状态集合$Q=\{1,2,3\}$ $A=\begin{bmatrix} 0.5,0.2,0.3 \\ 0.3,0.5,0.2 \\ 0.2,0.3,0.5 \end{bmatrix},B=\begin{bmatrix} 0.5,0.5\\ 0.4,0.6\\ 0.7,0.3 \end{bmatrix},\pi=(0.2,0.4,0.2)^T$ 若观测序列$O=(O_1,O_2,O_1)$，求最优状态序列$I=(i_1^*,i_2^*,i_3^*)$
   

解： 定义$\delta_t(i)$是所有长度为t、最终状态为i的、能得到指定观测序列的路径中，概率最大的路径的概率。 定义$\Psi_t(i)$是所有长度为t、最终状态为i的、能得到指定观测序列的路径中，最有可能的倒数第二个节点（倒数第二个时间点概率最大的状态）：$\Psi_t(i)=\argmax\limits_{i\le j\le N}\big[\delta_{t-1}(j)a_{ji}\big]$
根据维特比算法的核心思想，我们计算观测序列下的最优路径： 1. t=1时，$\delta_1(i)$是观测为$o_1$、状态为i的概率： $\delta_1(i)=\pi_ib_i(O_1),\ i=1,2,3$ 得$\delta_1(1)=0.2*0.5=0.1,\delta_1(2)=0.16,\delta_1(3)=0.28$ 记$\Psi_1(i)=0,\ i=1,2,3$ 2. t=2时： $\delta_2(i)=\max\limits_{1\le j\le3}\big[\delta_1(j)a_{ji}\big]b_i(o_2)$ $\Psi_2(i)=\argmax\limits_{1\le j\le3}\big[\delta_1(j)a_{ji}\big],i=1,2,3$ $\delta_2(1)=\max\limits_j\{0.1*0.5,0.16*0.3,0.28*0.2\},\Psi_2(1)=3$ 类似：$\delta_2(2)=0.0504,\Psi_2(2)=3,\delta_2(3)=0.042,\Psi_2(3)=3$ 3. t=3时： $\delta_3(i)=\max\limits_{1\le j\le3}\big[\delta_2(j)a_{ji}\big]b_i(o_3)$ $\Psi_3(i)=\argmax\limits_{1\le j\le3}\big[\delta_2(j)a_{ji}\big],i=1,2,3$ $\delta_3(1)=0.00756,\Psi_3(1)=2,\delta_3(2)=0.01008,\Psi_3(2)=2,\delta_3(3)=0.0147,\Psi_3(3)=3$ 最有可能的路径以$i_3^*=\argmax_i\big[\delta_3(i)\big]$为最终状态 4. 回溯其他时刻的最优节点： t=2时，$i_2^*=\Psi_3(i_3^*)=\Psi_3(3)=3$ t=1时，$i_1^*=\Psi_2(i_2^*)=\Psi_2(3)=3$ 因此最优状态序列是：$I=(i_1^*,i_2^*,i_3^*)=(3,3,3)$

4. HMM用法

1. 标注学习/序列标注 sequence tagging：对已观测到的数据序列O进行标注，标注序列I相当于隐变量

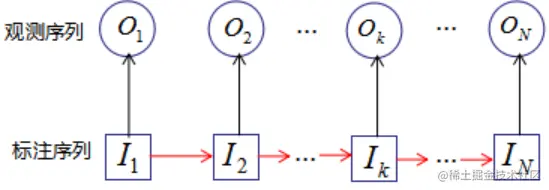
2. 语音识别：waveform是输出序列，匹配音素（状态）序列

3. 词性标注

4. 文本分析

5. 其他正文及脚注未提及的参考资料

1. Natural language processing: an introduction
2. 初学者也能看懂的隐马尔科夫模型介绍

Footnotes

1. 可参考我撰写的博文：变分推断（variational inference）/variational EM_诸神缄默不语的博客-CSDN博客 ↩