一、概述

1. 介绍

动态模型可以类比高斯混合模型这种静态模型，高斯混合模型的特点是“混合”，动态模型的特点是在“混合”的基础上加入了“时间”。动态模型包括多种模型：

$$Dynamic\; Model\left\{\begin{matrix} HMM \\ Kalman\; Filter\\ Particle\; Filter \end{matrix}\right.$$

隐马尔可夫模型是动态模型的一种，它的状态空间是离散的，而另外两种动态模型的状态空间是连续的。

2. 模型

隐马尔可夫模型的概率图模型如下：

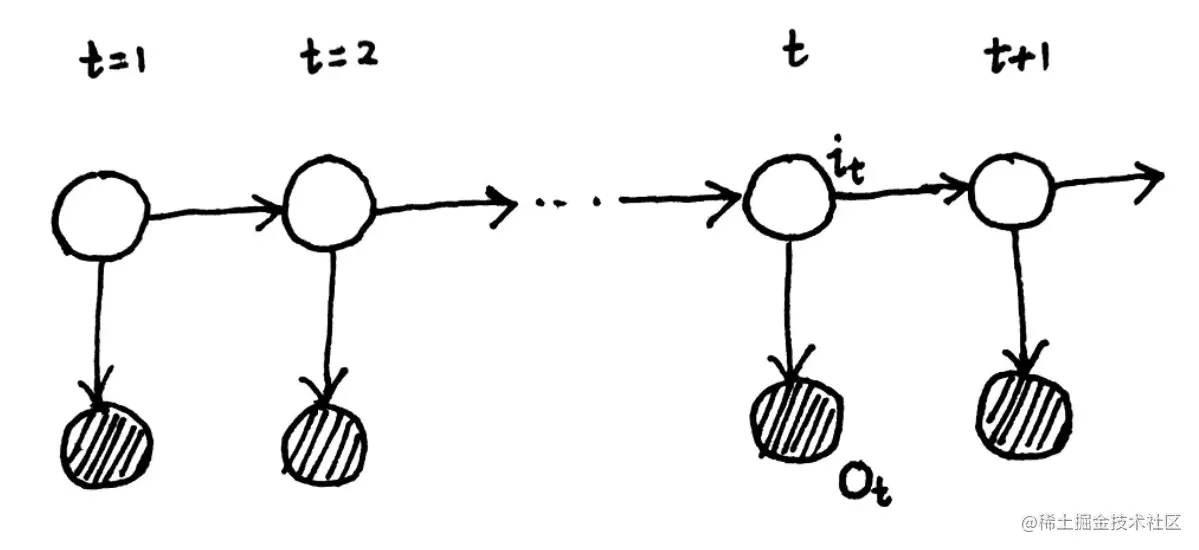
概率图模型

上图中$t$代表时刻，阴影部分为观测变量序列$O$，非阴影部分为状态变量序列$I$，另外我们定义观测变量取值的集合为$V$，状态变量取值的集合为$Q$：

$$O=o_{1},o_{2},\cdots ,o_{t}\rightarrow V=\left \{v_{1},v_{2},\cdots ,v_{m}\right \}\\ I=i_{1},i_{2},\cdots ,i_{t}\rightarrow Q=\left \{q_{1},q_{2},\cdots ,q_{n}\right \}$$

隐马尔可夫模型的参数用$\lambda$表达：

$$\lambda =(\pi ,A,B)$$

其中$\pi$为初始概率分布，是一个多维向量；$A$为状态转移矩阵；$B$为发射矩阵：

$$\pi =(\pi _{1},\pi _{2},\cdots ,\pi _{N}),\sum_{i=1}^{N}\pi _{i}=1\\ A=[a_{ij}],a_{ij}=P(i_{t+1}=q_{j}|i_{t}=q_{i})\\ B=[b_{j}(k)],b_{j}(k)=P(o_{t}=v_{k}|i_{t}=q_{j})$$

3. 两个假设

• 齐次马尔可夫假设

任意时刻的状态只依赖于前一时刻的状态，即：

$$P(i_{t+1}|i_{t},i_{t-1},\cdots ,i_{1},o_{t},o_{t-1},\cdots ,o_{1})=P(i_{t+1}|i_{t})$$

• 观测独立假设

任意时刻的观测只依赖于当前时刻的状态，即：

$$P(o_{t}|i_{t},i_{t-1},\cdots ,i_{1},o_{t-1},\cdots ,o_{1})=P(o_{t}|i_{t})$$

4. 三个问题

• Evaluation

已知模型的参数$\lambda =(\pi ,A,B)$，计算某个观测序列发生的概率，即求：

$$P(O|\lambda )$$

• Learning

已知观测序列，使用EM算法求参数$\lambda$：

$$\lambda _{MLE}=\underset{\lambda }{argmax}\; P(O|\lambda )$$

• Decoding

已知观测序列$O$和参数$\lambda$，求使概率$P(I|O)$最大的状态序列$I$，即：

$$\hat{I}=\underset{I}{argmax}\; P(I|O)$$

二、Evaluation问题

对于下图中的隐马尔可夫模型，Evaluation问题是在已知参数$\lambda$的情况下，求解$P(O|\lambda )$：

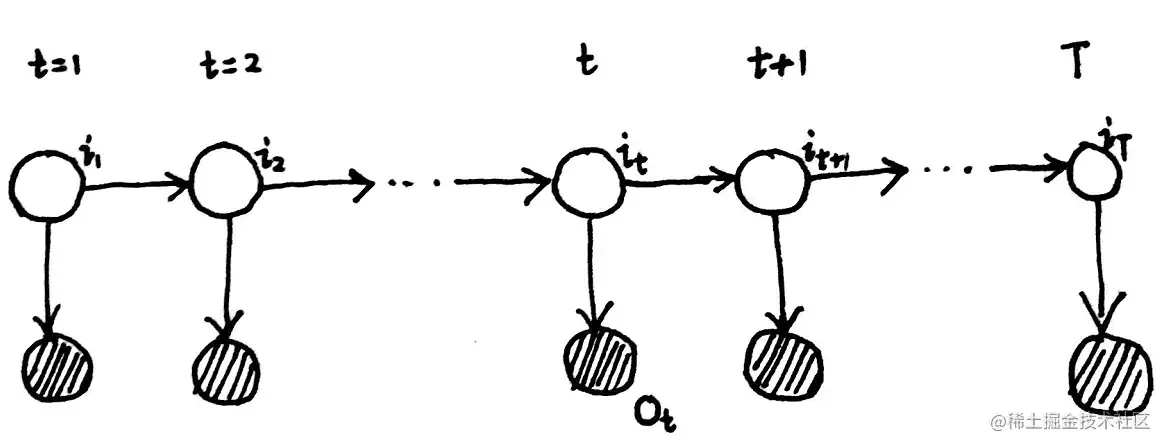
1. 前向算法

首先我们有：

$$P(O|\lambda )=\sum _{I}P(I,O|\lambda )=\sum _{I}P(O|I,\lambda )P(I|\lambda )$$

对于上式中的$P(I|\lambda )$，有：

$$P(I|\lambda )=P(i_{1},i_{2},\cdots ,i_{T}|\lambda )=P(i_{T}|i_{1},i_{2},\cdots ,i_{T-1},\lambda )\cdot P(i_{1},i_{2},\cdots ,i_{T-1}|\lambda )\\ 根据齐次Markov假设：\\ P(i_{t}|i_{1},i_{2},\cdots ,i_{t-1},\lambda )=P(i_{t}|i_{t-1})=a_{i_{t-1}i_{t}}\\ 所以：\\P(I|\lambda )=\pi (i_{1})\prod_{t=2}^{T}a_{i_{t-1}i_{t}}$$

对于上式中的$P(O|I,\lambda )$，有：

$$P(O|I,\lambda )=\prod_{t=1}^{T}b_{i_{t}}(o_{t})$$

因此可得：

$$P(O|\lambda )=\sum _{I}\pi (i_{1})\prod_{t=2}^{T}a_{i_{t-1}i_{t}}\prod_{t=1}^{T}b_{i_{t}}(o_{t})=\underset{复杂度:O(N^{T})}{\underbrace{\sum _{i_{1}}\sum _{i_{2}}\cdots \sum _{i_{T}}\pi (i_{1})\prod_{t=2}^{T}a_{i_{t-1}i_{t}}\prod_{t=1}^{T}b_{i_{t}}(o_{t})}}$$

上面的求和是对所有的观测变量求和，所以复杂度为$O(N^{T})$

下面记：

$$\alpha _{t}(i)=P(o_{1},o_{2},\cdots ,o_{t},i_{t}=q_{i}|\lambda )$$

所以：

$$\alpha _{T}(i)=P(O,i_{T}=q_{i}|\lambda )$$

所以可以得到：

$$P(O|\lambda )=\sum_{i=1}^{N}P(O,i_{t}=q_{i}|\lambda )=\sum_{i=1}^{N}\alpha _{T}(i)$$

对于$\alpha _{t+1}(j)$：

$$\alpha _{t+1}(j)=P(o_{1},\cdots ,o_{t},o_{t+1},i_{t+1}=q_{j}|\lambda )\\ =\sum_{i=1}^{N}P(o_{1},\cdots ,o_{t},o_{t+1},i_{t+1}=q_{j},i_{t}=q_{i}|\lambda )\\ =\sum_{i=1}^{N}{\color{Red}{P(o_{t+1}|o_{1},\cdots ,o_{t},i_{t}=q_{i},i_{t+1}=q_{j},\lambda )}}P(o_{1},\cdots ,o_{t},i_{t}=q_{i},i_{t+1}=q_{j}|\lambda )\\ =\sum_{i=1}^{N}{\color{Red}{P(o_{t+1}|i_{t+1}=q_{j},\lambda )}}P(o_{1},\cdots ,o_{t},i_{t}=q_{i},i_{t+1}=q_{j}|\lambda )\\ =\sum_{i=1}^{N}{\color{Red}{b_{j}(o_{t+1})}}{\color{Blue}{P(i_{t+1}=q_{j}|o_{1},\cdots ,o_{t},i_{t}=q_{i},\lambda )}}{\color{DarkOrange}{P(o_{1},\cdots ,o_{t},i_{t}=q_{i}|\lambda )}}\\ =\sum_{i=1}^{N}{\color{Red}{b_{j}(o_{t+1})}}{\color{Blue}{P(i_{t+1}=q_{j}|i_{t}=q_{i},\lambda )}}{\color{Orange}{\alpha _{t}(i)}}\\ =\sum_{i=1}^{N}{\color{Red}{b_{j}(o_{t+1})}}{\color{Blue}{a_{ij}}}{\color{Orange}{\alpha _{t}(i)}}$$

上式利用两个假设得到了一个递推公式，这个算法叫做前向算法，其复杂度为$O(TN^{2})$。

2. 后向算法

定义：

$$\beta _{t}(i)=P(o_{t+1},\cdots ,o_{T}|i_{t}=q_{i},\lambda )$$

所以：

$$P(O|\lambda )=P(o_{1},\cdots ,o_{T}|\lambda )\\ =\sum_{i=1}^{N}P(o_{1},\cdots ,o_{T},i_{1}=q_{i}|\lambda )\\ =\sum_{i=1}^{N}P(o_{1},\cdots ,o_{T}|i_{1}=q_{i},\lambda )\underset{\pi _{i}}{\underbrace{P(i_{1}=q_{i}|\lambda )}}\\ =\sum_{i=1}^{N}P(o_{1}|o_{2},\cdots ,o_{T},i_{1}=q_{i},\lambda )\underset{\beta _{1}(i)}{\underbrace{P(o_{2},\cdots ,o_{T}|i_{1}=q_{i},\lambda )}}\pi _{i}\\ =\sum_{i=1}^{N}P(o_{1}|i_{1}=q_{i},\lambda )\beta _{1}(i)\pi _{i}\\ =\sum_{i=1}^{N}b_{i}(o_{1})\beta _{1}(i)\pi _{i}$$

因此如果我们能找到$\beta _{t}(i)$到$\beta _{t+1}(j)$的递推式，就可以由通过递推得到$\beta _{1}(i)$，从而计算$P(O|\lambda )$：

$$\beta _{t}(i)=P(o_{t+1},\cdots ,o_{T}|i_{t}=q_{i},\lambda )\\ =\sum_{j=1}^{N}P(o_{t+1},\cdots ,o_{T},i_{t+1}=q_{j}|i_{t}=q_{i},\lambda )\\ =\sum_{j=1}^{N}{\color{Red}{P(o_{t+1},\cdots ,o_{T}|i_{t+1}=q_{j},i_{t}=q_{i},\lambda)}}{\color{Blue}{P(i_{t+1}=q_{j}|i_{t}=q_{i},\lambda )}}\\ =\sum_{j=1}^{N}{\color{Red}{P(o_{t+1},\cdots ,o_{T}|i_{t+1}=q_{j},\lambda)}}{\color{Blue}{a_{ij}}}\\ =\sum_{j=1}^{N}{\color{Orange}{P(o_{t+1}|o_{t+2},\cdots ,o_{T},i_{t+1}=q_{j},\lambda)}}{\color{Orchid}{P(o_{t+2},\cdots ,o_{T}|i_{t+1}=q_{j},\lambda)}}{\color{Blue}{a_{ij}}}\\ =\sum_{j=1}^{N}{\color{Orange}{P(o_{t+1}|i_{t+1}=q_{j},\lambda)}}{\color{Orchid}{\beta _{t+1}(j)}}{\color{Blue}{a_{ij}}}\\ =\sum_{j=1}^{N}{\color{Orange}{b_{j}(o_{t+1})}}{\color{Blue}{a_{ij}}}{\color{Orchid}{\beta _{t+1}(j)}}$$

上式中红色的一步变换利用了概率图模型中有向图head to tail结构的性质：

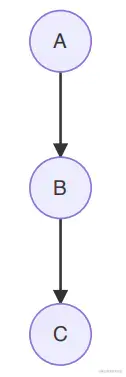
这种结构满足：

$$A\perp C|B\Leftrightarrow 若B被观测，则路径被阻塞。$$

到此为止便得到了递推式。这就是后向算法，其复杂度也为$O(TN^{2})$。

三、Learning问题

Learning问题的目标是求解参数$\lambda$，使用的是Baum Welch算法（也就是EM算法）。

EM算法的迭代公式如下：

$$\theta ^{(t+1)}=\underset{\theta }{argmax}\int _{Z}log\; P(X,Z|\theta )\cdot P(Z|X,\theta ^{(t)})\mathrm{d}Z$$

在隐马尔可夫模型中，隐变量$Z$即为$I$，观测变量$X$即为$O$，参数$\theta$即为$\lambda$，因此隐马尔可夫模型的EM算法迭代公式可以写为：

$$\lambda ^{(t+1)}=\underset{\lambda}{argmax}\sum _{I}log\; P(O,I|\lambda )\cdot P(I|O,\lambda ^{(t)})$$

上式中$P(I|O,\lambda ^{(t)})=\frac{P(O,I|\lambda ^{(t)})}{P(O|\lambda ^{(t)})}$，由于在Learning问题中，观测序列$O$是已知的，所以$P(O|\lambda ^{(t)})$是个常数，迭代公式可以写为：

$$\lambda ^{(t+1)}=\underset{\lambda}{argmax}\sum _{I}log\; P(O,I|\lambda )\cdot P(O,I|\lambda ^{(t)})$$

根据之前的计算对$Q$函数进行整理：

$$Q(\lambda ,\lambda ^{(t)})=\sum _{I}log\; P(O,I|\lambda )\cdot P(O,I|\lambda ^{(t)})\\ =\sum _{I}[log\pi (i_{1})\prod_{t=2}^{T}a_{i_{t-1}i_{t}}\prod_{t=1}^{T}b_{i_{t}}(o_{t})\cdot P(O,I|\lambda ^{(t)})]\\ =\sum _{I}[(log\pi (i_{1})+\sum_{t=2}^{T}log\; a_{i_{t-1}i_{t}}+\sum_{t=1}^{T}log\; b_{i_{t}}(o_{t}))\cdot P(O,I|\lambda ^{(t)})$$

接下来以求解$\pi ^{(t+1)}$为例展示迭代的过程：

$$\pi ^{(t+1)}=\underset{\pi }{argmax}\; Q(\lambda ,\lambda ^{(t)})\\ =\underset{\pi }{argmax}\sum _{I}log\; \pi (i_{1})\cdot P(O,I|\lambda ^{(t)})\\ =\underset{\pi }{argmax}\sum _{i_{1}}\sum _{i_{2}}\cdots \sum _{i_{T}}log\; \pi (i_{1})\cdot P(O,i_{1},i_{2},\cdots ,i_{T}|\lambda ^{(t)})\\ =\underset{\pi }{argmax}\sum _{i_{1}}log\; \pi (i_{1})\cdot P(O,i_{1}|\lambda ^{(t)})\\ =\underset{\pi }{argmax}\sum _{i=1}^{N}log\; \pi _{i}\cdot P(O,i_{1}=q_{i}|\lambda ^{(t)})$$

结合对$\pi$的约束$\sum_{i=1}^{N}\pi _{i}=1$，构建拉格朗日函数：

$$L(\pi ,\eta )=\sum _{i=1}^{N}log\; \pi _{i}\cdot P(O,i_{1}=q_{i}|\lambda ^{(t)})+\eta (\sum_{i=1}^{N}\pi _{i}-1)$$

然后对$\pi _{i}$求导：

$$\frac{\partial L}{\partial \pi _{i}}=\frac{1}{\pi _{i}}P(O,i_{1}=q_{i}|\lambda ^{(t)})+\eta =0 \\ \Rightarrow P(O,i_{1}=q_{i}|\lambda ^{(t)})+\pi _{i}\eta =0\\ \Rightarrow \sum_{i=1}^{N}[P(O,i_{1}=q_{i}|\lambda ^{(t)})+\pi _{i}\eta ]=0\\ \Rightarrow P(O|\lambda ^{(t)})+\eta =0\\ \Rightarrow \eta =-P(O|\lambda ^{(t)})\\ 代入P(O,i_{1}=q_{i}|\lambda ^{(t)})+\pi _{i}\eta =0\\ \Rightarrow \pi ^{(t+1)}_{i}=\frac{P(O,i_{1}=q_{i}|\lambda ^{(t)})}{P(O|\lambda ^{(t)})}$$

同样地，$A^{(t+1)}$和$B^{(t+1)}$都以同样的方法求出，然后不断迭代直至收敛，最终求得模型的参数。

四、Decoding问题

Decoding问题是指已知观测序列$O$和参数$\lambda$，求使概率$P(I|O)$最大的状态序列$I$，即：

$$\hat{I}=\underset{I}{argmax}\; P(I|O)$$

我们采用动态规划的思想来求解这个问题(Viterbi)，首先定义：

$$\delta _{t}(i)={\color{Red}{\underset{i_{1},i_{2},\cdots ,i_{t-1}}{max}}}P(o_{1},o_{2},\cdots ,o_{t},i_{1},i_{2},\cdots ,i_{t-1},i_{t}=q_{i})$$

由于参数$\lambda$是已知的，为简便起见省略了$\lambda$，接下来我们需要找到$\delta _{t+1}(j)$和$\delta _{t}(i)$之间的递推式：

$$\delta _{t+1}(j)=\underset{i_{1},i_{2},\cdots ,i_{t}}{max}P(o_{1},o_{2},\cdots ,o_{t+1},i_{1},i_{2},\cdots ,i_{t},i_{t+1}=q_{j})\\ ={\color{Red}{\underset{1\leq i\leq N}{max}}}\delta _{t}(i)a_{ij}b_{j}(o_{t+1})$$

由此我们就找到了动态规划的递推式，同时我们还需要记录路径（因为全局最优唯一，但最优路径不一定唯一），因此定义：

$$\psi _{t+1}(j)={\color{Red}{\underset{1\leq i\leq N}{argmax}}}\; \delta _{t}(i)a_{ij}$$

因此：

$$max\; P(I|O)=max\; \delta _{t}(i)$$

使$P(I|O)$最大的$\delta _{t}(i)$指$t$时刻$i_t=q_i$，然后由$\psi _{t}(i)$得到$t-1$时刻$i_{t-1}$的取值，然后继续得到前一时刻的$i_{t-2}$时刻的取值，最终得到整个序列$I$。

五、总结

HMM 是⼀种动态模型（Dynamic Model），是由混合树形模型和时序结合起来的⼀种模型（类似 GMM + Time）。对于类似 HMM 的这种状态空间模型（State Space Model），普遍的除了学习任务（采⽤ EM ）外，还有推断任务。

使用$X$代表观测序列，$Z$代表隐变量序列，$\lambda$代表参数。这一类模型需要求解的问题的大体框架为：

接下来对Filtering&Smoothing&Prediction问题做一些说明，下面使用$x_{1:t}$代表$x_{1},x_{2},\cdots ,x_{t}$，同时也省略已知参数$\lambda$。

1. Filtering问题

$$P(z_{t}|x_{1:t})=\frac{P(x_{1:t},z_{t})}{P(x_{1:t})}=\frac{P(x_{1:t},z_{t})}{\sum _{z_{t}}P(x_{1:t},z_{t})} \propto P(x_{1:t},z_{t})=\alpha _{t}$$

因此使用Forward Algorithm来解决Filtering问题。

Filtering问题通常出现在online learning中，当新进入一个数据，可以计算概率$P(z_{t}|x_{1:t})$。

2. Smoothing问题

$$P(z_{t}|x_{1:T})=\frac{P(x_{1:T},z_{t})}{P(x_{1:T})}=\frac{P(x_{1:T},z_{t})}{\sum _{z_{t}}P(x_{1:T},z_{t})}$$

其中：

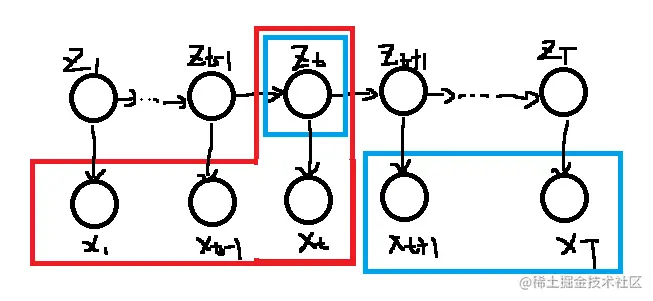
$$P(x_{1:T},z_{t})=P(x_{1:t},x_{t+1:T},z_{t})\\ ={\color{Red}{P(x_{t+1:T}|x_{1:t},z_{t})}}\cdot \underset{\alpha _{t}}{\underbrace{P(x_{1:t},z_{t})}}\\ =\underset{\beta _{t}}{\underbrace{{\color{Red}{P(x_{t+1:T}|z_{t})}}}}\cdot \alpha _{t}\\ =\alpha _{t}\beta _{t}$$

红色这一步是使用了有向图的D划分的方法，有关讲解参照9.概率图模型。这里我们定义A集合为$x_{1:t}$，B集合为$x_{t+1:T}$，C集合为$z_t$，通过D划分的方法我们可以知道$x_{A}\perp x_{B}|x_{C}$，即$x_{t+1:T}$与$x_{1:t}$是相互独立的。

由上面的式子我们可以得出：

$$P(z_{t}|x_{1:T})\propto P(x_{1:T},z_{t})=\alpha _{t}\beta _{t}$$

因此解决Smoothing问题的算法叫做Forward-Backward Algorithm。

Smoothing问题通常出现在offline learning中，当知道全部观测数据时，来计算概率$P(z_{t}|x_{1:T})$。

3. Prediction问题

$$P(z_{t+1}|x_{1:t})=\sum _{z_{t}}P(z_{t+1},z_{t}|x_{1:t})\\ =\sum _{z_{t}}P(z_{t+1}|z_{t},x_{1:t})\cdot P(z_{t}|x_{1:t})\\ =\sum _{z_{t}}P(z_{t+1}|z_{t})\cdot \underset{Filtering}{\underbrace{P(z_{t}|x_{1:t})}}$$

上式应用了齐次马尔可夫假设将预测$P(z_{t+1}|x_{1:t})$的问题进行了转化，使用转移概率和求解Filtering问题的方法就可以计算这个概率。

$$P(x_{t+1}|x_{1:t})=\sum _{z_{t+1}}P(x_{t+1},z_{t+1}|x_{1:t})\\ =\sum _{z_{t+1}}P(x_{t+1}|z_{t+1},x_{1:t})\cdot P(z_{t+1}|x_{1:t})\\ =\sum _{z_{t+1}}P(x_{t+1}|z_{t+1})\cdot \underset{Precition}{\underbrace{P(z_{t+1}|x_{1:t})}}$$

上式应用了观测独立假设将预测$P(x_{t+1}|x_{1:t})$的问题进行了转化，使用发射概率和求解上一个Prediction问题的方法就可以计算这个概率。

“开启掘金成长之旅！这是我参与「掘金日新计划 · 2 月更文挑战」的第 13 天，点击查看活动详情”