C++实现二叉树的定义与操作

homeskating
130 阅读4分钟
头文件及常量定义
#include<stdio.h>
#include<stdlib.h>
#include<stdarg.h>
#include<iostream>
#include<iterator>
using namespace std;
#define TElemType char
#define Status int
#define SUCCESS 1
#define ERROR -1
#define OVERFLOW -2
结构体
//二叉树的二叉链表存储表示
typedef struct BitNode
{
	TElemType data;
	struct BitNode* lchild, * rchild;
}BiTNode, * BiTree;
构造空二叉树
//构造空二叉树
Status InitBiTree(BiTree& T) {
	T = nullptr;
	return SUCCESS;
}
销毁二叉树
/*
销毁二叉树T
*/
Status DestroyBiTree(BiTree& T) {
	if ((T)->lchild)
		DestroyBiTree(T->lchild);
	if ((T)->rchild)
		DestroyBiTree(T->rchild);
	free(T);
	T = NULL;
	return SUCCESS;
}
先序队列创建二叉树
/*
* 先序队列创建二叉树
*/
Status CreateBiTree(BiTree& S) {
	TElemType ch;
	scanf("%c", &ch);
	if (ch == ' ') {
		S = nullptr;
	}
	else
	{
		S = (BiTree)malloc(sizeof(BiTNode));
		if (!S)
			exit(OVERFLOW);
		S->data = ch;
		CreateBiTree(S->lchild);
		CreateBiTree(S->rchild);
	}
	return SUCCESS;
}
清空二叉树
void ClearBiTree(BiTree& T) {
	if (T)
	{
		if (T->lchild) {
			ClearBiTree(T->lchild);
		}
		if (T->rchild)
		{
			ClearBiTree(T->rchild);
		}
		free(T);
		T = NULL;
	}
}
判断二叉树是否为空
const char* BiTreeEmpty(BiTree T) {
	const char* emptyMessage = "树为空！";
	const char* haveMessage = "树不为空";
	if (T)
	{
		return haveMessage;
	}
	else {
		return emptyMessage;
	}
}
返回二叉树深度
/*
返回二叉树的深度
*/
int BiTreeDepth(BiTree T) {
	int i, j;
	if (!T)
	{
		return 0;
	}
	if (T->lchild)
	{
		i = BiTreeDepth(T->lchild);
	}
	else {
		i = 0;
	}
	if (T->rchild)
	{
		j = BiTreeDepth(T->rchild);
	}
	else
	{
		j = 0;
	}
	return i > j ? i + 1 : j + 1;
}
打印二叉树的根元素
/*
打印二叉树T的根元素
*/
Status Root(BiTree T) {
	cout << T->data << endl;
	//printf("根元素为：%s\n", cout);
	return SUCCESS;
}
判断二叉树是否有元素e
/*
判断树是否有e元素
*/
Status Value(BiTree T, TElemType e) {
	if (T->data == e)
	{
		return SUCCESS;
	}
	else
	{
		int i = 0, j = 0;
		if (T->lchild)
		{
			i = Value(T->lchild, e);
		}
		if (T->rchild)
		{
			j = Value(T->rchild, e);
		}
		if (i || j) {
			return SUCCESS;
		}
		else {
			return ERROR;
		}
		return ERROR;
	}
}
将结点e的值赋为value
/*
将结点e的值赋为value
*/
Status Assign(BiTree& T, TElemType e, TElemType value) {
	if (T->data == e)
	{
		T->data = value;
		return SUCCESS;
	}
	else
	{
		int i = 0, j = 0;
		if (T->lchild)
		{
			i = Assign(T->lchild, e, value);
		}if (T->rchild)
		{
			j = Assign(T->rchild, e, value);
		}if (i || j)
		{
			return SUCCESS;
		}
		else {
			return ERROR;
		}
		return ERROR;
	}
}
打印结点e的双亲，否则返回错误
Status Parent(BiTree T, TElemType e) {
	if (T->lchild && T->lchild->data == e)
	{
		printf("双亲结点为：%c\n", T->data);
		return SUCCESS;
	}
	else if (T->rchild && T->rchild->data == e)
	{
		printf("双亲结点为：%c\n", T->data);
		return SUCCESS;
	}
	else
	{
		if (T->lchild)
		{
			Parent(T->lchild, e);
		}
		if (T->rchild)
		{
			Parent(T->rchild, e);
		}
	}
	return 0;
}
打印结点e的左孩子
/*
打印结点e的左孩子，若e无左孩子，则返回错误
*/
Status LeftChild(BiTree T, TElemType e) {
	if (T->data == e && T->lchild)
	{
		printf("左孩子结点为：%c\n", T->lchild->data);
		return SUCCESS;
	}
	else
	{
		if (T->lchild)
		{
			LeftChild(T->lchild, e);
		}
		if (T->rchild)
		{
			LeftChild(T->rchild, e);
		}
	}
}
打印结点e的右孩子
Status RightChild(BiTree T, TElemType e) {
	if (T->data == e && T->rchild)
	{
		printf("右孩子结点为:%c\n", T->rchild->data);
		return SUCCESS;
	}
	else
	{
		if (T->lchild)
		{
			RightChild(T->lchild, e);
		}
		if (T->rchild)
		{
			RightChild(T->rchild, e);
		}
	}
}
打印e的左兄弟
Status LeftSibling(BiTree T, TElemType e) {
	if (T->rchild != NULL)
	{
		if (T->lchild && T->rchild->data == e)
		{
			printf("左兄弟结点为:%c\n", T->lchild->data);
			return SUCCESS;
		}
		else
		{
			if (T->lchild)
			{
				LeftSibling(T->lchild, e);
			}
			if (T->rchild)
			{
				LeftSibling(T->rchild, e);
			}
		}
	}
	else
	{
		if (T->lchild)
		{
			LeftSibling(T->lchild, e);
		}
		if (T->rchild)
		{
			LeftSibling(T->rchild, e);
		}
	}

	return ERROR;
}
打印e的右兄弟
Status RightSibling(BiTree T, TElemType e) {
	if (T->lchild != NULL)
	{
		if (T->rchild && T->lchild->data == e)
		{
			printf("右兄弟结点为：%c\n", T->rchild->data);
			return SUCCESS;
		}
		else
		{
			if (T->lchild)
			{
				RightSibling(T->lchild, e);
			}
			if (T->rchild)
			{
				RightSibling(T->rchild, e);
			}
		}
	}
	else
	{
		if (T->lchild)
		{
			RightSibling(T->lchild, e);
		}
		if (T->rchild)
		{
			RightSibling(T->rchild, e);
		}
	}
	return ERROR;
}
插入孩子结点
/*
插入孩子结点
*/
Status InsertChild(BiTree p, int LR, BiTree c) {
	if (LR == 0)
	{
		/*
		若c的右子树为空，c成为p的左子树，
		p的原左子树变成c的右子树
		*/
		c->rchild = p->lchild;
		p->lchild = c;
	}
	else
	{
		/*
		若c的右子树为空，c的右子树变成p的右子树，
		p的原右子树变成c的右子树。
		*/
		c->rchild = p->rchild;
		p->rchild = c;
	}
	return SUCCESS;
}
删除结点的左或右子树
/*
根据LR为0或1，删除T中p所指结点的左或右子树
*/
Status DeleteChild(BiTree T, BiTree p, int LR) {
	if (LR == 0)
	{
		//删除p的左子树
		DestroyBiTree(p->lchild);
	}
	else
	{
		//删除p的右子树
		DestroyBiTree(p->rchild);
	}
	return SUCCESS;
}
main方法调用
int main(void) {
	//测试数据：ABC  DE G  F
	BiTree biTree = nullptr, insertBiTree = nullptr;
	int initResult = InitBiTree(biTree);
	printf("initResult=%d\n", initResult);
	int createBiTree = CreateBiTree(biTree);
	printf("createBiTree=%d\n", createBiTree);
	fseek(stdin, 0, SEEK_SET);
	const char* emptyMessage = BiTreeEmpty(biTree);
	printf("emptyMessage=%s\n", emptyMessage);
	int depthNum = BiTreeDepth(biTree);
	printf("depthNum=%d\n", depthNum);
	int rootResult = Root(biTree);
	printf("rootResult=%d\n", rootResult);
	int valueResult = Value(biTree, 'A');
	printf("valueResult=%d\n", valueResult);
	int assignResult = Assign(biTree, 'F', 'H');
	printf("assignResult=%d\n", assignResult);
	Parent(biTree, 'C');
	LeftChild(biTree, 'E');
	RightChild(biTree, 'B');
	LeftSibling(biTree, 'D');
	RightSibling(biTree, 'E');
	//printf("insertInitBiTree=%d\n", InitBiTree(insertBiTree));
	int insertCreateResult = CreateBiTree(insertBiTree);
	printf("insertCreateBiTree=%d\n", insertCreateResult);
	int insertChildResult = InsertChild(biTree, 0, insertBiTree);
	printf("insertChildResult=%d\n", insertChildResult);
	int deleteChildResult = DeleteChild(biTree, insertBiTree, 0);
	printf("deleteChildResult=%d\n", deleteChildResult);
	int destoryBiTree = DestroyBiTree(biTree);
	printf("destoryBiTree=%d\n", destoryBiTree);
}
运行截图

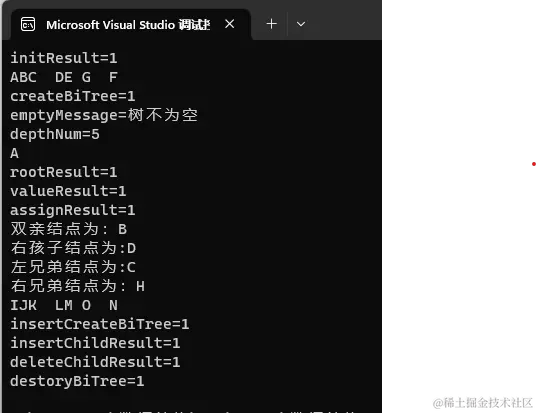
二叉树的定义与操作运行图.png

编写代码中遇到的问题与解决方案
  1. 在代码中使用了scanf("%c",&ch),该函数会把所有输入的字符获得。换行符也会被传入，初始化第二棵树时就会因为结点不足，而无法初始化第二棵二叉树。
  2. 二叉树的操作大多是使用递归来查找双亲，左右子，左右兄弟结点等。
avatar
文章
阅读
粉丝