“开启掘金成长之旅！这是我参与「掘金日新计划 · 2 月更文挑战」的第 3 天，点击查看活动详情”

机器学习的三个基本因素

机器学习是从有限的观测数据中学习（或“猜测”）出具有一般性的规律，并可以将总结出来的规律推广应用到未观测样本上。

机器学习方法可以粗略地分为三个基本要素：模型、学习准则、优化算法。

模型

对于一个机器学习任务，首先要确定其输入空间 $x$ 和输出空间 $y$ ，不同机器学习任务的主要区别在于输出空间不同。在二分类问题中 $y ={+1,-1}$ ，在C分类问题中 $y={1,2,...,C}$ ,而在回归问题中 $y=R$ .

输入空间 $x$ 和输出空间 $y$ 构成了一个样本空间，对于样本空间中的样本 $(x,y)\in x \times y$ ，假定 $x$ 和 $y$ 之间的关系可以通过一个未知的真实映射函数 $y =g(x)$ 或真实条件概率分布 $p_r(y/x)$ 来描述。机器学习的目标是找到一个模型来近似真实映射函数 $g(x)$ 或真实条件概率分布 $p_r(y/x)$ 。

由于我们不知道真实的映射函数 $g(x)$ 或条件概率分布 $p_r(y/x)$ 的具体形式因而只能根据经验来假设一个函数集合 $\mathcal F$ ,称为假设空间( Hypothesis Space)，然后通过观测其在训练集 $D$ 上的特性从中选择一个理想的假设(Hypothesis ) $f^*\in \mathcal F$ 。

假设空间 $F$ 通常为一个参数化的函数族

\mathcal F=\{f(\mathbf x;\theta)|\theta\in\mathbb R^D\}

其中 $f(\mathbf x;\theta)$ 是参数为 $\theta$ 的函数，也称为模型(Model),D为参数的数量。

常见的假设空间可以分为线性和非线性两种，对应的模型 $f$ 也分别称为线性模型和非线性模型.

线性模型

线性模型的假设空间为一个参数化的线性函数族,即

\quad f(\mathbf{x};\theta)=\mathbf{w}^{\intercal}\mathbf{x}+b,

其中参数 $\theta$ 包含了权重向量 $w$ 和偏置 $b$ .

非线性模型

广义的非线性模型可以写为多个非线性基函数 $\phi(x)$ 的线性组合

f(\boldsymbol{x};\theta)=\boldsymbol{w}^{\top}\phi(\boldsymbol{x})+b

其中 $\phi(\mathbf{x})=[\phi_{1}(\mathbf{x}),\phi_{2}(\mathbf{x}),\cdots,\phi_{K}(\mathbf{x})]^{\intercal}$ 为K个非线性基函数组成的向量，参数 $\theta$ 包含了权重向量 $w$ 和偏置 $b$ 。

如果 $\phi(x)$ 本身为可学习的基函数，比如

\phi_{k}(\boldsymbol{x})=h(\boldsymbol{w}_{k}^{\intercal}\phi^{\prime}(\boldsymbol{x})+b_{k}),\forall1\leq k\leq K

其中 $h(\cdot)$ 为非线性函数， $\phi'(x)$ 为另一组基函数， $w_k$ 和 $b_k$ 为可学习的参数，则 $f(\mathbf{x};\theta)$ 就等价于神经网络模型。

学习准则

令训练集 ${\cal D}=\{(x^{(n)},y^{(n)})\}_{n=1}^{N}$ 是由N个独立同分布的(Independent and dentically Distributed,IID)样本组成,即每个样本 $(x,y)\in x \times y$ 是从 $x$ 和 $y$ 的联合空间中按照某个未知分布 $p_r(x,y)$ 独立地随机产生的。这里要求样本分布 $p_r(x,y)$ 必须是固定的(虽然可以是未知的),不会随时间而变化。如果 $p_r(x,y)$ 本身可变的话,就无法通过这些数据进行学习.

一个好的模型 $f(\mathbf{x},\theta^{*})$ 应该在所有 $(x,y)$ 的可能取值上都与真实映射函数 $y = g(x)$ 一致,即

|f(\boldsymbol{x},\theta^*)-y|<\varepsilon,\quad\forall(\boldsymbol{x},y)\in\boldsymbol{x}\times y,

或与真实条件概率分布 $p_r(y/x)$ 一致,即

|f_y(\mathbf x,\theta^*)-p_r(y|\mathbf x)|<\epsilon,\quad\forall(\mathbf x,y)\in\mathbf x\times y,

其中 $\epsilon$ 是一个很小的正数, $f_y(x,\theta^*)$ 为模型预测的条件概率分布中 $y$ 对应的概率。

模型 $f(x;\theta)$ 的好坏可以通过期望风险( Expected Risk ) $R(\theta)$ 来衡量,其定义为

\mathcal{R}(\theta)=\mathbb{E}_{(x,y)-p_r(x,y)}[\mathcal{L}\big(y,f(\mathbf{x};\theta)\big)]

其中 $p_r(x,y)$ 为真实的数据分布, $\mathcal{L}(y,f(x;\theta))$ 为损失函数,用来量化两个变量之间的差异.

损失函数

损失函数是一个非负实数函数,用来量化模型预测和真实标签之间的差异下面介绍几种常用的损失函数.

0-1损失函数 最直观的损失函数是模型在训练集上的错误率，即0-1 损失函数( 0-1 Loss Function ) :

\mathcal{L}\big(y,f(\mathbf{x};\theta)\big)=\left\{\begin{array}{c}0&\textrm{if}y=f(\mathbf{x};\theta)\\ 1&\textrm{if}y\neq f(\mathbf{x};\theta)\\ =I(y\neq f(\mathbf{x};\theta)),\end{array}\right.

平方损失函数 平方损失函数(Quadratic Loss Function)经常用在预测标签 $y$ 为实数值的任务中,定义为

\mathcal{L}\bigl(y,f(\mathbf{x};\theta)\bigr)=\dfrac{1}{2}\Bigl(y-f(\mathbf{x};\theta)\Bigr)^2.

平方损失函数一般不适用于分类问题。

交叉损失函数 交叉熵损失函数( Cross-Entropy Loss Function)一般用于分类问题. 假设样本的标签 $y\in \{1,...,C\}$ 为离散的类别,模型 $f(\mathbf{x};\theta)\in[0,1]^{C}$ 的输出为类别标签的条件概率分布,即

p(y=c|\mathbf{x};\theta)=f_c(\mathbf{x};\theta)

并满足

f_c(\mathbf{x};\theta)\in[0,1],\quad\sum\limits_{c=1}^{C}f_c(\mathbf{x};\theta)=1

我们可以用一个C维的one-hot 向量 $y$ 来表示样本标签。设样本的标签为k,那么标签向量 $y$ 只有第k维的值为1,其余元素的值都为0.标签向量y可以看作样本标签的真实条件概率分布 $p_r(y/x)$ 即第c维(记为 $y_c$$ 1\leq c\leq C$ )是类别为c的真实条件概率.假设样本的类别为 $k$ ,那么它属于第k类的概率为1属于其他类的概率为0.

对于两个概率分布，一般可以用交叉熵来衡量它们的差异.标签的真实分布y和模型预测分布 $f(\mathbf{x};\theta)$ 之间的交叉熵为

\begin{array}{r}\mathcal{L}(\boldsymbol{y},f(\boldsymbol{x};\boldsymbol{\theta}))=-\boldsymbol{y}^{\tau}\log f(\boldsymbol{x};\boldsymbol{\theta})\\ =-\sum_{c=1}^{C}y_{c}\log f_{c}(\boldsymbol{x};\boldsymbol{\theta}).\end{array}

比如对于三分类问题，一个样本的标签向量为 $y =[0,0,1]^T$ ，模型预测的标签分布为 $f(x;\theta) =[0.3,0.3,0.4]^T$ ，则它们的交叉熵为 $-(0 \times log(0.3) + 0\times log(0.3) + 1 \times log(0.4)) = - log(0.4)$

因为 $y$ 为one-hot向量,公式也可以写为

\mathcal{L}\big(y,f(\mathbf{x};\theta)\big)=-\log f_y(\mathbf{x};\theta)

其中 $f_y(\mathbf{x};\theta)$ 可以看作真实类别 $y$ 的似然函数。因此，交叉损失函数也就是负对数似然函数( Negative Log-Likelihood )。

Hinge 损失函数 对于二分类问题，假设y的取值为 ${-1,+1}$ ， $f(\mathbf{x};\theta)\in R$ .

Hinge损失函数(Hinge Loss Function)为

\begin{array}{c}\mathcal{L}\big(y,f(\mathbf{x};\theta)\big)=\max\big(0,1-y f(\mathbf{x};\theta)\big)\\ \triangleq\big[1-y f(\mathbf{x};\theta)\big]_+,\end{array}

其中 $\left[x\right]_{+}=\mathrm{max}(0,x)$

风险最小化准则

一个好的模型 $f(\mathbf{x};\theta)$ 应当有一个比较小的期望错误，但由于不知道真实的数据分布和映射函数，实际上无法计算其期望风险 $\mathcal{R}(\theta)$ . 给定一个训练集 ${\cal D}=\{(x^{(n)},y^{(n)})\}_{n=1}^{N}$ ,我们可以计算的是经验风险( Empirical Risk ),即在训练集上的平均损失:

\mathcal{R}_{D}^{emp}(\theta)=\dfrac{1}{N}\sum\limits_{n=1}^{N}\mathcal{L}(y^{(n)},f(\mathbf{x}^{(n)};\theta))

因此,一个切实可行的学习准则是找到一组参数 $\theta^*$ 使得经验风险最小,即

\theta^*=\arg\limits_\theta\min\mathcal{R}_D^{emp}(\theta)

这就是经验风险最小化( Empirical Risk Minimization,ERM)准则。

过拟合 根据大数定理可知，当训练集大小 $|D|$ 趋向于无穷大时,经验风险就趋向于期望风险.然而通常情况下,我们无法获取无限的训练样本,并且训练样本往往是真实数据的一个很小的子集或者包含一定的噪声数据，不能很好地反映全部数据的真实分布.经验风险最小化原则很容易导致模型在训练集上错误率很低,但是在未知数据上错误率很高.这就是所谓的过拟合(Overfitting).

过拟合问题往往是由于训练数据少和噪声以及模型能力强等原因造成的.为了解决过拟合问题，一般在经验风险最小化的基础上再引入参数的正则化( Regularization) 来限制模型能力，使其不要过度地最小化经验风险，这种准则就是结构风险最小化(Structure Risk Minimization,SRM) 准则:

\begin{aligned}\theta^x&=\arg\min\mathcal R_D^{stract}(\theta)\\\\ &=\arg\min\mathcal R_D^{ener}(\theta)+\frac12\lambda\|\theta\|^2\\\\ &=\arg\min\frac1N\sum_{n=1}^N\mathcal L(y^{(n)},f(x^{(n)};\theta))+\frac12\lambda\|\theta\|^2,\end{aligned}

其中 $\|\theta\|$ 是 ${\boldsymbol{\ell}}_{2}$ 范数的正则化项,用来减少参数空间,避免过拟合;用来控制正则化的强度.

正则化项也可以使用其他函数，比如 ${\boldsymbol{\ell}}_{1}$ 范数。 ${\boldsymbol{\ell}}_{1}$ 范数的入通常会使得参数有一定稀疏性，因此在很多算法中也经常使用.从贝叶斯学习的角度来讲，正则化是引入了参数的先验分布,使其不完全依赖训练数据。

和过拟合相反的一个概念是欠拟合(Underfitting) ，即模型不能很好地拟合训练数据,在训练集上的错误率比较高.欠拟合一般是由于模型能力不足造成的.下图给出了欠拟合和过拟合的示例.

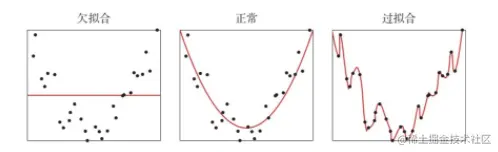
总之,机器学习中的学习准则并不仅仅是拟合训练集上的数据,同时也要使得泛化错误最低.给定一个训练集,机器学习的目标是从假设空间中找到一个泛化错误较低的“理想”模型,以便更好地对未知的样本进行预测,特别是不在训练集中出现的样本.

因此,我们可以将机器学习看作一个从有限、高维、有噪声的数据上得到更一般性规律的泛化问题。

机器学习的三个基本要素