• 前缀和是为了求数组中的一段数据的和
• 本质是用空间换时间
• 后期每次查询的时间复杂度为o(1)

模板

一维前缀和

• 前期初始化的时间复杂度为o(n)

S[i] = a[1] + a[2] + ... a[i]
a[l] + ... + a[r] = S[r] - S[l - 1]

二维前缀和

• 思想：容斥原理

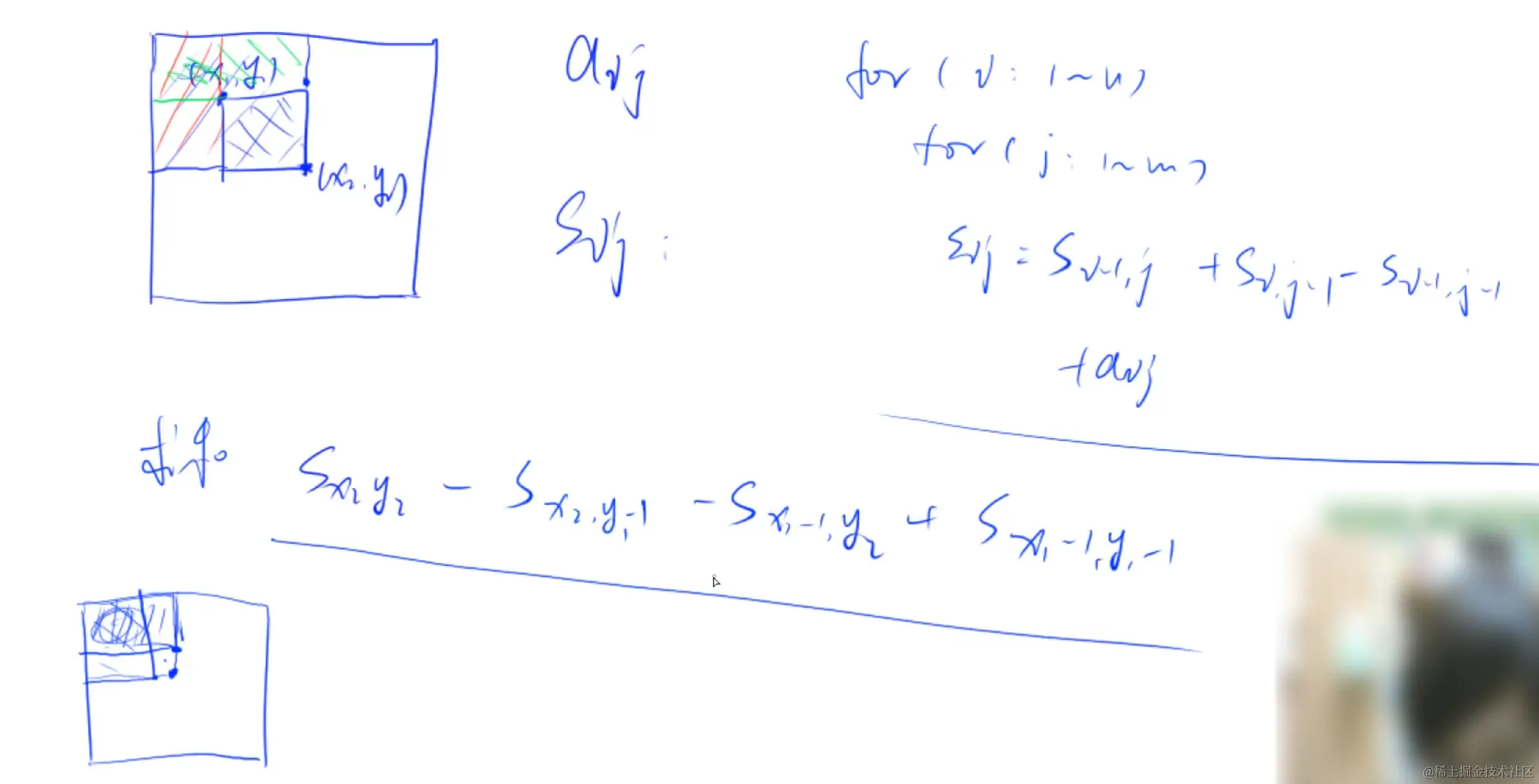
S[i, j] = 第i行j列格子左上部分所有元素的和
S[i,j] = S[i - 1, j] + S[i, j - 1] - S[i - 1, j - 1] + a[i, j]
以(x1, y1)为左上角，(x2, y2)为右下角的子矩阵的和为：
S[x2, y2] - S[x1 - 1, y2] - S[x2, y1 - 1] + S[x1 - 1, y1 - 1]

练习

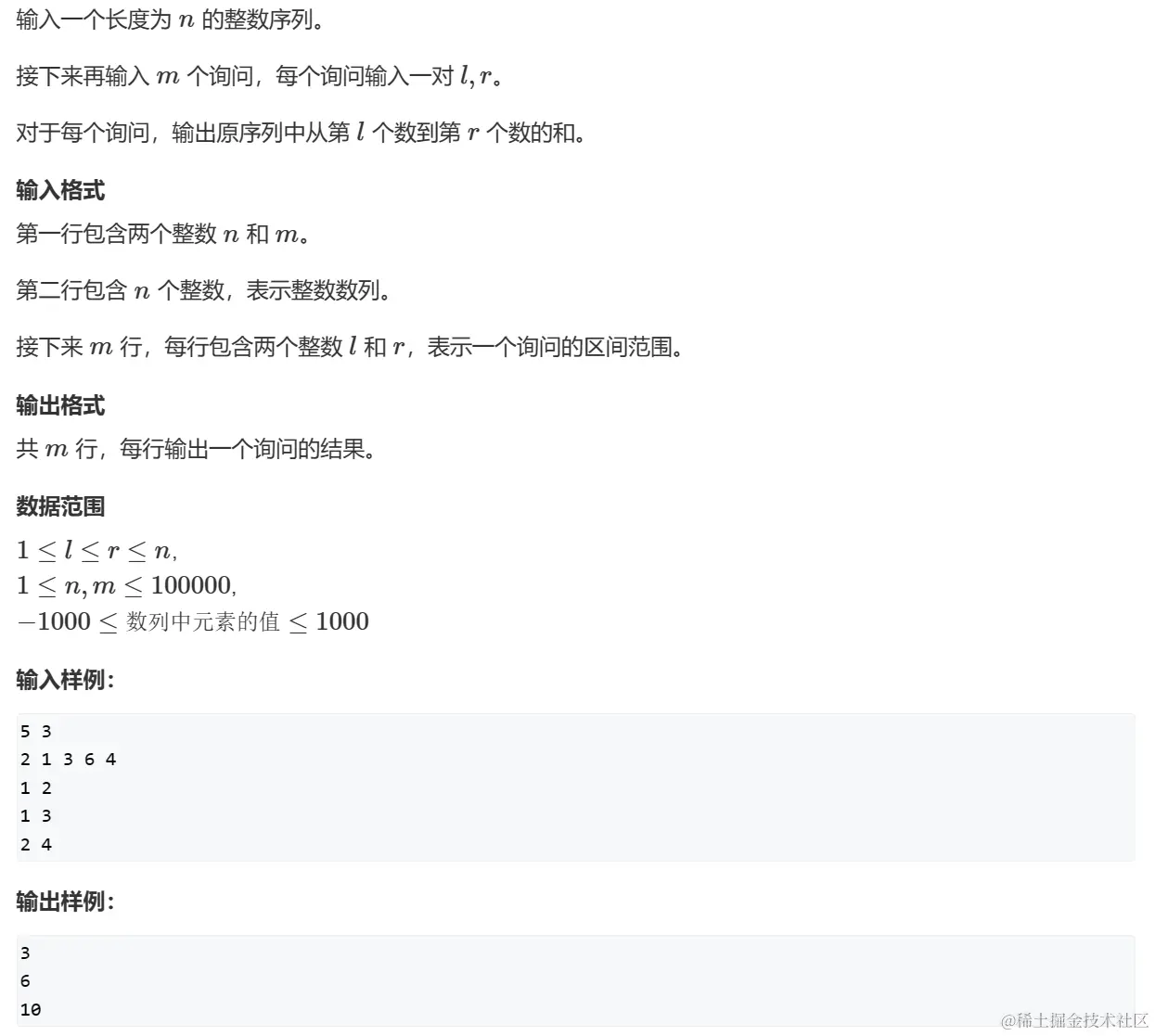
01 前缀和

• 题目

• 题解

import java.io.*;

public class Main {
    public static final int N = 100010;
    public static int[] a = new int[N];
    public static int[] S = new int[N];

    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        String[] str1 = br.readLine().split(" ");
        int n = Integer.parseInt(str1[0]);
        int m = Integer.parseInt(str1[1]);
        String[] str2 = br.readLine().split(" ");
        for (int i = 1; i <= n; i++) {
            a[i] = Integer.parseInt(str2[i - 1]);
        }
        for (int i = 1; i <= n; i++) {
            S[i] = S[i - 1] + a[i];
        }
        while (m-- > 0) {
            String[] str3 = br.readLine().split(" ");
            int l = Integer.parseInt(str3[0]);
            int r = Integer.parseInt(str3[1]);
            System.out.println(S[r] - S[l - 1]);
        }
        br.close();
    }
}

02 子矩阵的和

• 题目

• 题解

import java.io.*;

public class Main{
    public static final int N = 1010;
    public static int[][] a = new int[N][N];
    public static int[][] S = new int[N][N];
    public static int n, m, q;

    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        String[] str1 = br.readLine().split(" ");
        n = Integer.parseInt(str1[0]);
        m = Integer.parseInt(str1[1]);
        q = Integer.parseInt(str1[2]);

        for (int i = 1; i <= n; i++) {
            String[] str2 = br.readLine().split(" ");
            for (int j = 1; j <= m; j++) {
                a[i][j] = Integer.parseInt(str2[j - 1]);
            }
        }
        //事实上这里并不需要新的S矩阵，直接在原先的a矩阵上覆盖就行
        for (int i = 1; i <= n; i++) {
            for (int j = 1; j <= m; j++) {
                S[i][j] = S[i - 1][j] + S[i][j - 1] - S[i - 1][j - 1] + a[i][j];
            }
        }
        while (q-- > 0) {
            String[] str3 = br.readLine().split(" ");
            int x1 = Integer.parseInt(str3[0]);
            int y1 = Integer.parseInt(str3[1]);
            int x2 = Integer.parseInt(str3[2]);
            int y2 = Integer.parseInt(str3[3]);
            System.out.println(S[x2][y2] - S[x1 - 1][y2] - S[x2][y1 - 1] + S[x1 - 1][y1 - 1]);
        }
    }
}