一、概述

对于高斯混合模型的假设，首先来看以下两个例子。

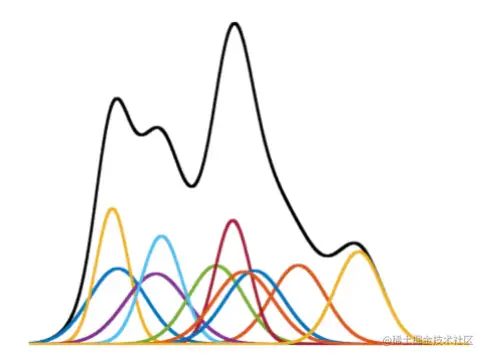
首先，让我们以一维数据为例。如下图所示，我们可以将多个独立的高斯模型通过加权叠加在一起，从而得到一个高斯混合模型。这种混合模型明显具有比单个高斯模型更高的拟合能力：

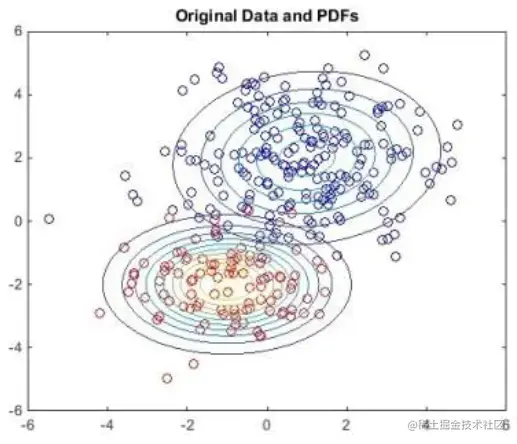
接下来，我们以二维数据为例。在下图中，我们可以看到存在两个数据聚集区域，这两个区域对应的概率分布会有两个峰值。高斯混合模型可以视为生成模型，其数据生成过程可以认为是首先选择一个高斯分布，然后从这个被选中的高斯分布中生成数据：

综合上述两个例子，我们可以从两种角度来描述高斯混合模型：

1. 几何角度：加权平均

可以认为高斯混合模型是将多个高斯分布加权平均而成的模型：

$$p(x)=\sum_{k=1}^{K}\alpha _{k}N(\mu _{k},\Sigma _{k}),\sum_{k=1}^{K}\alpha _{k}=1$$

2. 混合模型（或者生成模型）角度

可以认为高斯混合模型是一种含有隐变量的生成模型：

$x$:观测变量

$z$:隐变量

$z$是隐变量，表示对应的样本$x$属于哪一个高斯分布，其概率分为如下表：

$z$	$C_1$	$C_2$	$\cdots$	$C_k$
$p$	$p_1$	$p_2$	$\cdots$	$p_k$

可以认为这里的概率$p_k$就是几何角度加权平均中的权重，两种角度的解释其实是一个意思。

我们可以画出高斯混合模型的概率图：

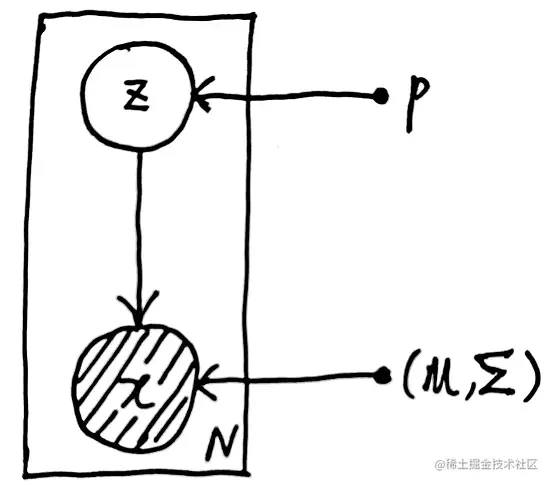
实心点p代表模型的一个参数，空心圈Z代表随机变量，右下角的$N$代表样本个数。

生成过程：随机变量$Z$的参数是p，$p=(p_1,p_2,...,p_k)$（k为该高斯混合模型中高斯分布的个数），再在选择出的高斯分布中随机取样x样本点，将这个过程重复$N$次即为生成了N个样本点。

二、尝试用极大似然估计来求解

$X$ :observed data $\rightarrow X=\left(x_1, x_2, \cdots, x_N\right)$ $(X, Z)$ :comlete data $\theta$ :parameter

$\rightarrow \theta=\left\{p_1, p_2, \cdots, p_k, \mu_1, \mu_2, \cdots, \mu_k, \Sigma_1, \Sigma_2, \cdots, \Sigma_k\right\}, \sum_{i=1}^K p_k=1$

以上为我们的数据以及需要求解的参数。接下来我们表示一下概率 $p(x)$ :

$$p(x)=\sum _{z}p(x,z)\\ =\sum _{k=1}^{K}p(x,z=C_{k})\\ =\sum _{k=1}^{K}p(z=C_{k})\cdot p(x|z=C_{k})\\ =\sum _{k=1}^{K}p_{k}\cdot N(x|\mu _{k},\Sigma _{k})$$

然后我们使用极大似然估计法求解这个参数估计问题。首先告知结论：极大似然估计法无法求解含有隐变量的参数估计问题，或者说不能得到解析解。接下来来看为什么不能用极大似然估计法来求解：

$$\hat{\theta }_{MLE}=\underset{\theta }{argmax}\; log\; p(X)\\ =\underset{\theta }{argmax}\; log\prod_{i=1}^{N}p(x_{i})\\ =\underset{\theta }{argmax}\sum_{i=1}^{N}log\; p(x_{i})\\ =\underset{\theta }{argmax}\sum_{i=1}^{N}{\color{Red}{log\sum _{k=1}^{K}}}p_{k}\cdot N(x_{i}|\mu _{k},\Sigma _{k})$$

极大似然估计法无法获得解析解，主要原因是$log$函数中出现了求和符号。我们更倾向于$log$函数内部存在乘法的情况，因为这样可以将其拆分为两项相加，从而更易于求解。但是，如果在对特定参数求导之后，出现了$log$函数内求和的情况，那么这就意味着需要满足$log$函数中一长串累加项的和等于0的条件，这是一件困难的事情。当然，我们可以使用梯度下降法进行求解，但对于包含隐变量的模型，使用EM算法更为合适。

三、使用EM算法求解

由于使用EM算法需要用到联合概率$p(x,z)$和后验$p(z|x)$，所有我们首先写出这两个概率的表示：

$$p(x,z)=p(z)p(x|z)=p_{z}\cdot N(x|\mu _{z},\Sigma _{z})\\ p(z|x)=\frac{p(x,z)}{p(x)}=\frac{p_{z}\cdot N(x|\mu _{z},\Sigma _{z})}{\sum_{k=1}^{K}p_{k}\cdot N(x|\mu _{k},\Sigma _{k})}$$

1. E step

$$Q(\theta ,\theta ^{t})=\sum _{Z}log\; p(X,Z|\theta )\cdot p(Z|X,\theta ^{t})\\ =\sum _{z_{1}z_{2}\cdots z_{N}}log\; \prod_{i=1}^{N}p(x_{i},z_{i}|\theta )\cdot \prod_{i=1}^{N} p(z_{i}|x_{i},\theta ^{t})\\ =\sum _{z_{1}z_{2}\cdots z_{N}}\sum_{i=1}^{N}log\; p(x_{i},z_{i}|\theta )\cdot \prod_{i=1}^{N} p(z_{i}|x_{i},\theta ^{t})\\ =\sum _{z_{1}z_{2}\cdots z_{N}}[log\; p(x_{1},z_{1}|\theta )+log\; p(x_{2},z_{2}|\theta )+\cdots +log\; p(x_{i},z_{i}|\theta )]\cdot \prod_{i=1}^{N} p(z_{i}|x_{i},\theta ^{t})$$

对于上式展开的每一项，我们可以进行化简：

$$\sum _{z_{1}z_{2}\cdots z_{N}}log\; p(x_{1},z_{1}|\theta )\prod_{i=1}^{N} p(z_{i}|x_{i},\theta ^{t})\\ =\sum _{z_{1}z_{2}\cdots z_{N}}log\; p(x_{1},z_{1}|\theta )\cdot p(z_{1}|x_{1},\theta ^{t})\prod_{i=2}^{N} p(z_{i}|x_{i},\theta ^{t})\\ =\sum _{z_{1}}log\; p(x_{1},z_{1}|\theta )\cdot p(z_{1}|x_{1},\theta ^{t})\sum _{z_{2}z_{3}\cdots z_{N}}\prod_{i=2}^{N} p(z_{i}|x_{i},\theta ^{t})\\ =\sum _{z_{1}}log\; p(x_{1},z_{1}|\theta )\cdot p(z_{1}|x_{1},\theta ^{t})\sum _{z_{2}z_{3}\cdots z_{N}}p(z_{2}|x_{2},\theta ^{t})p(z_{3}|x_{3},\theta ^{t})\cdots p(z_{N}|x_{N},\theta ^{t})\\ =\sum _{z_{1}}log\; p(x_{1},z_{1}|\theta )\cdot p(z_{1}|x_{1},\theta ^{t})\underset{=1}{\underbrace{\sum _{z_{2}}p(z_{2}|x_{2},\theta ^{t})}}\underset{=1}{\underbrace{\sum _{z_{3}}p(z_{3}|x_{3},\theta ^{t})}}\cdots \underset{=1}{\underbrace{\sum _{z_{N}}p(z_{N}|x_{N},\theta ^{t})}}\\ =\sum _{z_{1}}log\; p(x_{1},z_{1}|\theta )\cdot p(z_{1}|x_{1},\theta ^{t})$$

同样的我们可以得到：

$$\sum _{z_{1}z_{2}\cdots z_{N}}log\; p(x_{i},z_{i}|\theta )\prod_{i=1}^{N} p(z_{i}|x_{i},\theta ^{t})=\sum _{z_{i}}log\; p(x_{i},z_{i}|\theta )\cdot p(z_{i}|x_{i},\theta ^{t})$$

继续对$Q(\theta ,\theta ^{t})$进行化简可以得到：

$$Q(\theta ,\theta ^{t})=\sum _{z_{1}}log\; p(x_{1},z_{1}|\theta )\cdot p(z_{1}|x_{1},\theta ^{t})+\cdots +\sum _{z_{N}}log\; p(x_{N},z_{N}|\theta )\cdot p(z_{N}|x_{N},\theta ^{t}) \\ =\sum_{i=1}^{N}\sum _{z_{i}}log\; p(x_{i},z_{i}|\theta )\cdot p(z_{i}|x_{i},\theta ^{t}) \\ =\sum_{i=1}^{N}\sum _{z_{i}}log\; [p_{z_{i}}\cdot N(x_{i}|\mu _{z_{i}},\Sigma _{z_{i}})]\cdot \frac{p_{z_{i}}^{t}\cdot N(x_{i}|\mu _{z_{i}}^{t},\Sigma _{z_{i}}^{t})}{\sum_{k=1}^{K}p_{k}^{t}\cdot N(x_{i}|\mu _{k}^{t},\Sigma _{k}^{t})}\\ (\frac{p_{z_{i}}^{t}\cdot N(x_{i}|\mu _{z_{i}}^{t},\Sigma _{z_{i}}^{t})}{\sum_{k=1}^{K}p_{k}^{t}\cdot N(x_{i}|\mu _{k}^{t},\Sigma _{k}^{t})}与\theta 无关，暂时写作p(z_{i}|x_{i},\theta ^{t}))\\ =\sum_{i=1}^{N}\sum _{z_{i}}log\; [p_{z_{i}}\cdot N(x_{i}|\mu _{z_{i}},\Sigma _{z_{i}})]\cdot p(z_{i}|x_{i},\theta ^{t})\\ =\sum _{z_{i}}\sum_{i=1}^{N}log\; [p_{z_{i}}\cdot N(x_{i}|\mu _{z_{i}},\Sigma _{z_{i}})]\cdot p(z_{i}|x_{i},\theta ^{t})\\ =\sum_{k=1}^{K}\sum_{i=1}^{N}log\; [p_{k}\cdot N(x_{i}|\mu _{k},\Sigma _{k})]\cdot p(z_{i}=C_{k}|x_{i},\theta ^{t})\\ =\sum_{k=1}^{K}\sum_{i=1}^{N}[log\; p_{k }+log\; N(x_{i}|\mu _{k},\Sigma _{k})]\cdot p(z_{i}=C_{k}|x_{i},\theta ^{t})$$

2. M step

EM算法的迭代公式为：

$$\theta ^{t+1}=\underset{\theta }{argmax}\; Q(\theta ,\theta ^{t})$$

下面以求解$p^{t+1}=(p_{1}^{t+1},p_{2}^{t+1},\cdots ,p_{K}^{t+1})^{T}$为例，来看如何进行迭代求解，以下是求解的迭代公式：

$$p_{k}^{t+1}=\underset{p_{k}}{argmax}\sum_{k=1}^{K}\sum_{i=1}^{N}log\; p_{k }\cdot p(z_{i}=C_{k}|x_{i},\theta ^{t}),s.t.\; \sum_{k=1}^{K}p_{k}=1$$

于是可以转化为以下约束优化问题：

$$\begin{cases} \underset{p}{min}-\sum_{k=1}^{K}\sum_{i=1}^{N}log\; p_{k }\cdot p(z_{i}=C_{k}|x_{i},\theta ^{t})\\ s.t.\; \sum_{k=1}^{K}p_{k}=1 \end{cases}$$

然后使用拉格朗日乘子法进行求解：

$$L(p,\lambda )=-\sum_{k=1}^{K}\sum_{i=1}^{N}log\; p_{k }\cdot p(z_{i}=C_{k}|x_{i},\theta ^{t})+\lambda (\sum_{k=1}^{K}p_{k}-1)\\ \frac{\partial L}{\partial p_{k}}=-\sum_{i=1}^{N}\frac{1}{p_{k}}\cdot p(z_{i}=C_{k}|x_{i},\theta ^{t})+\lambda \overset{\triangle }{=}0\\ \Rightarrow -\sum_{i=1}^{N}p(z_{i}=C_{k}|x_{i},\theta ^{t})+p_{k}^{t+1}\lambda =0\\ \overset{k=1,2,\cdots ,K}{\Rightarrow }-\underset{=N}{\underbrace{\sum_{i=1}^{N}\underset{=1}{\underbrace{\sum_{k=1}^{K}p(z_{i}=C_{k}|x_{i},\theta ^{t})}}}}+\underset{=1}{\underbrace{\sum_{k=1}^{K}p_{k}^{t+1}}}\lambda =0\\ \Rightarrow -N+\lambda =0\\ \Rightarrow \lambda =N\\ 代入-\sum_{i=1}^{N}p(z_{i}=C_{k}|x_{i},\theta ^{t})+p_{k}^{t+1}\lambda =0得\\ -\sum_{i=1}^{N}p(z_{i}=C_{k}|x_{i},\theta ^{t})+p_{k}^{t+1}N=0\\ \Rightarrow p_{k}^{t+1}=\frac{\sum_{i=1}^{N}p(z_{i}=C_{k}|x_{i},\theta ^{t})}{N}$$

这里以求解$p^{t+1}$为例展示了M step的求解过程，其他参数也按照极大化Q函数的思路就可以求解，求得一轮参数后要继续迭代求解直至收敛。

“开启掘金成长之旅！这是我参与「掘金日新计划 · 2 月更文挑战」的第 9 天，点击查看活动详情”