什么是超平面分离

超平面分离是线性分类器，有监督的判别式的参数模型。

超平面分离的主要思想是确定不同类别数据之间的分隔平面 $\omega^Tx+b=0$

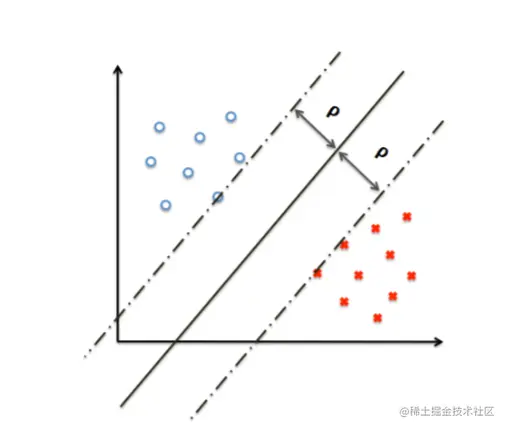
核心公式

\rho(\boldsymbol{w}, b):=\min _{i=1, \ldots, n} \frac{\left|\boldsymbol{w}^T \boldsymbol{x}_i+b\right|}{\|\boldsymbol{w}\|}

\begin{aligned} & \max _{\boldsymbol{w}, b} \rho(\boldsymbol{w}, b) \\ & \text { s.t. } y_i\left(\boldsymbol{w}^T \boldsymbol{x}_i+b\right)>0 \quad \forall i . \end{aligned}

其中 $\rho(w,b)$ 表示点到平面的最短距离的绝对值，目标是使最短距离最大。

通过，求出 $m = \min |\omega^T x_i+b|$ ,

\omega = \frac{\omega}{m}\\ b = \frac{b}{m}\\

所有的超平面公式都可以被写为规范形式,即

y_i\left(\boldsymbol{w}^T \boldsymbol{x}_i+b\right) \geq \quad \forall i\\ y_i\left(\boldsymbol{w}^T \boldsymbol{x}_i+b\right) =1 \quad \exist i

在转化为规范形式后，原式可转化为

\max \rho(\boldsymbol{w}, b)\\ \min _{i=1, \ldots, n} \rho(\boldsymbol{w}, b)=\frac{1}{\|\boldsymbol{w}\|}

进一步的，

\begin{aligned} & \min \left\|\omega \right\|^2 \\ & \text { s.t. } y_i\left(\boldsymbol{w}^T \boldsymbol{x}_i+b\right)\geq 1 \quad \forall i . \end{aligned}

通过求解该优化问题即可求得分离的超平面

实际应用中，有很多数据并不是线性可分的，如

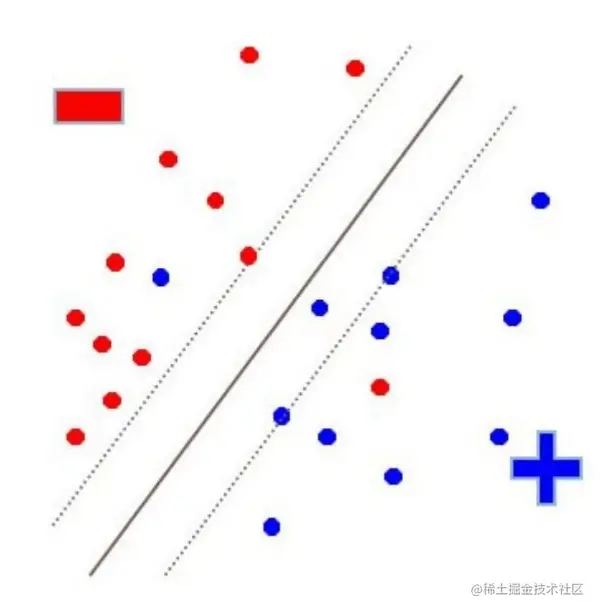
这种情况下，我们有两种选择，一种是使用非线性分类器进行分类，另一种是容忍部分误差，继续使用线性分类器求出超平面，即最优软间隔超平面。我们下面将讨论最优软间隔超平面.

\begin{aligned} & \min _{\boldsymbol{w}, b, \boldsymbol{\xi}} \frac{1}{2}\|\boldsymbol{w}\|^2+\frac{C}{n} \sum_{i=1}^n \xi_i \\ & \text { s.t. } y_i\left(\boldsymbol{w}^T \boldsymbol{x}_i+b\right) \geq 1-\xi_i, \quad \forall i \\ & \quad \xi_i \geq 0, \quad \forall i . \end{aligned}

其中， $\xi_i$ 为我们引入的松弛项，允许数据出现在超平面最小间隔以内 $\xi_i$ 的距离.

可转化为如下问题求解

\min _{\boldsymbol{w}, b} \frac{\lambda}{2}\|\boldsymbol{w}\|^2+\frac{1}{n} \sum \max \left(0,1-y_i\left(\boldsymbol{w}^T \boldsymbol{x}_i+b\right)\right)